Toepassingen

Omstreeks 1918 ontdekte de Franse wiskundige Gaston Julia een zeer grillige meetkundige structuur, waarvan hij zich toen nauwelijks een visuele voorstelling kon maken. Pas in de laatste jaren zijn wiskundigen met behulp van snelle computers met grote grafische mogelijkheden in staat om deze structuren - die de wiskundige Mandelbrot fractalen is gaan noemen - zichtbaar te maken.

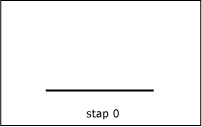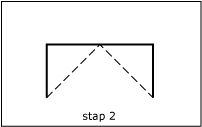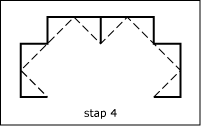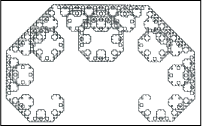
De fractal van Levy bijvoorbeeld is te construeren door te beginnen met een (niet te klein) lijnstuk en dat te vervangen door een half vierkant waarvan de uiteinden samenvallen met die van het lijnstuk. Vervolgens herhaal je dat met de twee lijnstukjes die je gekregen hebt, enzovoorts, tot in het oneindige door.

De Levy-fractal kun je beschrijven met een stelsel complexe functies.
Begin met de complexe getallen z met Im z = 0 en Re z uit [0,4].
Pas op elke z deze twee functies toe:
L(z) = 12(1 + i)z
R(z) = 12(1 - i)z + 2(1 + i)
Teken de beide beeldlijnstukken. Pas op elk der beeldlijnstukken opnieuw beide functies toe. Je krijgt dan vier beeldlijnstukjes, waarop je opnieuw beide functies loslaat. En zo ad infinitum.

Als je googlet op "fractal" vind je veel sites waar prachtige voorbeelden van fractalen zijn te zien...