Theorie

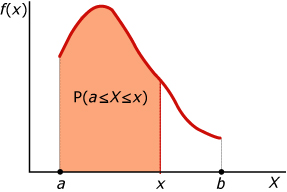
Een toevalsvariabele X die alle reële waarden uit een bepaald interval [a,b] kan aannemen noem je een continue stochast. Kun je daarbij een kansdichtheidsfunctie bepalen, dan worden de bijbehorende kansen weergegeven door een deel van de oppervlakte onder de kromme die bij deze functie hoort. Dergelijke kansen bereken je daarom door integreren.
Bijvoorbeeld P(a ≤ X ≤ x) = ${\displaystyle \underset{a}{\overset{x}{\int }}f(x)\text{d}x}$.
Daarvoor moet je dan wel een functievoorschrift voor f(t) hebben. Anders moet je de oppervlakte schatten m.b.v. de tekening.

Omdat de totale kans 1 moet zijn, is ${\displaystyle \underset{a}{\overset{b}{\int }}f(x)\text{d}x}$ = 1.
Hieraan moet elke kansdichtheidsfunctie f voldoen.
Een kansverdeling kun je bij een continue stochast niet maken.