Voorbeeld

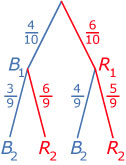
Uit een vaas met 6 rode en 4 blauwe knikkers worden zonder teruglegging twee knikkers getrokken.
Je krijgt alleen de tweede knikker te zien, die is blauw.
Hoe groot is de kans dat de eerste knikker rood is?

Antwoord

Het maakt bij de tweede trekking verschil of de eerst getrokken knikker rood of blauw was. Door niet terug te leggen is immers de oorspronkelijke situatie gewijzigd. De tweede trekking is daarom afhankelijk van de eerste.

De gevraagde kans is P(R₁|B₂).
Omdat P(B₂) = P(R₁ en B₂) + P(B₁ en B₂) =
= P(R₁) · P(B₂|R₁) + P(B₁) · P(B₂|B₁) = $\frac{6}{10}$ · $\frac{4}{9}$ + $\frac{4}{10}$ · $\frac{3}{9}$ = $\frac{36}{90}$
is gemiddeld in 36 van de 90 trekkingen de tweede bal blauw.
In 4 · 6 = 24 van die trekkingen was de eerste bal rood.
De gevraagde kans is daarom $\frac{24}{36}$.

Merk op dat je deze kans kunt berekenen vanuit P(B₂) en P(R₁ en B₂):
P(R₁|B₂) = $\frac{\text{P}(R_1\text{ en }{B}_2)}{\text{P}(B_2)}$.
Ga na dat dit netjes past bij de algemene productregel voor afhankelijke gebeurtenissen.