Voorbeeld
Uit een vaas met 6 rode en 4 blauwe knikkers worden met teruglegging twee knikkers getrokken.
Hoe groot is de kans op een rode en een blauwe knikker?
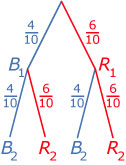
Antwoord
Het maakt bij de tweede trekking niet uit of de eerst getrokken knikker rood of blauw was. Door het terugleggen is immers de oorspronkelijke situatie weer hersteld. De tweede trekking is daarom onafhankelijk van de eerste.
Je kunt dus de productregel voor onafhankelijke kansen gebruiken:
- de kans dat je eerst een rode en dan een blauwe knikker trekt is:
P(R1 en B2) = P(R1) · P(B2) = · = - de kans dat je eerst een blauwe en dan een rode knikker trekt is:
P(B1 en R2) = P(B1) · P(R2) = · =