Theorie
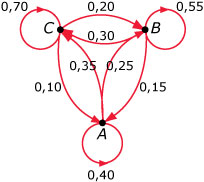
De overgangen tussen verschillende situaties A, B en C in een vaste tijdsperiode kunnen worden beschreven met een overgangsgraaf.
Dit is een gerichte graaf met luswegen. Dat komt omdat er behalve van overgang van de éne situatie naar de andere ook sprake is van in dezelfde situatie blijven. De getallen bij de pijlen zijn overgangskansen die daarom alleen waarden van 0 t/m 1 kunnen aannemen. Het totaal van de overgangskansen vanuit één bepaalde situatie is altijd 1.

Bij een overgangsgraaf past een overgangsmatrix M.
In de tabel zie je hoe daarbij het "van ... naar ..." is geregeld. Die keuze bepaalt hoe je met matrixvermenigvuldiging de verdeling over de verschillende situaties telkens één periode verder berekent. Dit betekent bovendien dat de som van de kentallen in elke kolom 1 is.
Als de 3×1-matrix V0 de verdeling van de aantallen over de drie situaties voorstelt, dan zijn de aantallen na één periode V1 = M · V0, na twee periodes V2 = M · V1, enzovoorts. (Je moet wel denken om een passende en steeds gelijke volgorde van aantallen en kansen bij de verschillende situaties.)
Blijf je zo doorrekenen, dan vormen de verdelingen een zogenaamde Markov-keten.
Soms leidt dit doorrekenen tot een evenwichtssituatie, waarin de aantallen voor A, B en C niet meer veranderen.