Theorie

Bij exponentiële groei moet je per tijdseenheid steeds met hetzelfde getal vermenigvuldigen. Dit getal heet de groeifactor die bij die tijdseenheid hoort. Als g de groeifactor is dan geldt: g > 0.
Om met negatieve exponenten en/of gebroken exponenten te kunnen werken zijn de volgende afspraken nodig:

• negatieve exponenten: g^–n = $\frac{1}{g^n}$
• gebroken exponenten: $g^{\frac{1}{n}}=\sqrt[n]{g}$

Beide afspraken passen helemaal in de rekenregels voor machten, bijvoorbeeld:
g^–n = g^0–n = $\frac{g^0}{g^n}=\frac{1}{g^n}$.

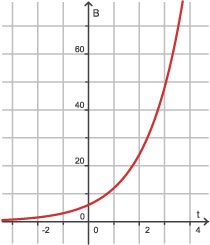
Je hebt nu gezien dat een macht g^a voor g > 0 betekenis heeft als de exponent a en positief getal, nul, een negatief getal of een gebroken getal is. In feite mag a elk reëel getal zijn. En daarom kunnen bij exponentiële groei grafieken worden getekend in de vorm van een nette vloeiende kromme lijn. Hier zie je de grafiek bij B = 6 · 2^t.