Uitleg

Voor een rit in een taxi betaal je:

• voorrijkosten € 3,20
• per gereden kilometer € 1,20

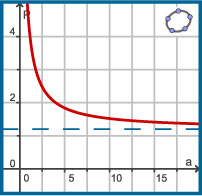
De grafiek van deze functie heeft geen nulpunten, of extremen, maar wel geldt:

• Als a (het aantal gereden kilometers) heel groot wordt, benaderen de functiewaarden het getal 1,20. Je ziet dat als je een tabel bij de functie maakt.
  Dit betekent dat de grafiek steeds dichter bij de lijn P = 1,20 komt te liggen. Deze lijn heet de horizontale asymptoot van de grafiek van P.
• Als a dicht bij 0 komt, worden de functiewaarden steeds groter: P(0,1) = 33,20; P(0,01) = 321,20; P(0,001) = 3201,20; P(0,0001) = 32001,20; etc.
  Maar je mag voor a geen 0 invullen: delen door 0 levert geen reëel getal op.
  Dit betekent dat de grafiek steeds dichter bij de lijn a = 0 (de verticale as) komt te liggen. Dit is de verticale asymptoot van de grafiek van P.