Voorbeeld

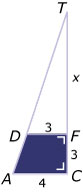
Hier zie je een afgeknotte piramide ABC.DEF. Het grondvlak ΔABC is rechthoekig met een rechte hoek bij hoekpunt C. De ribbe CF staat loodrecht op het grondvlak ABC en het bovenvlak DEF.
AC = 4, BC = CF = DF = 3.
Bereken de lengte van ribbe CT van de oorspronkelijke piramide ABC.T.

Antwoord

Schets ΔACT met daarin lijnstuk DF.
Omdat CF loodrecht op zowel AC als DF staat is AC // DF en hebben de driehoeken ACT en DFT gelijke hoeken. Beide driehoeken zijn gelijkvormig.

Omdat DF = $\frac{3}{4}$ · AC is ook TF = $\frac{3}{4}$ · TC.
Noem je TF = x, dan is TC = x + 3.
En dus is x = $\frac{3}{4}$(x + 3).
Hieruit volgt x = 9.

En dus is CT = 12.