Voorbeeld

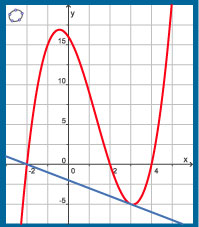
Stel een vergelijking op van de raaklijn aan de grafiek van de functie g(x) = (x² – 4)(x – 4) voor x = 3.

Antwoord

Voor de vergelijking van de raaklijn heb je het hellingsgetal g'(3) nodig. Dat kun je met behulp van je grafische rekenmachine vinden. Maar het kan ook met behulp van differentiëren.

Eerst schrijf je het functievoorschrift als een som (verschil) van machtsfuncties en constante functies. Haakjes uitwerken geeft:

g(x) = x³ – 4x² – 4x¹ + 16.

De afgeleide is daarom:

g'(x) = 3 · x² – 4 · 2 · x¹ – 4 · 1 · x⁰ + 0 = 3x² – 8x – 4.

Je vindt daarmee: g'(3) = –1.
En de raaklijn krijgt een vergelijking van de vorm: y = –1x + b.
Omdat g(3) = –5 gaat de raaklijn door (3, –5).
Invullen in de vergelijking van de raaklijn geeft: –5 = –3 + b en dus b = –2.
De vergelijking van de raaklijn wordt: y = –x – 2.