Theorie

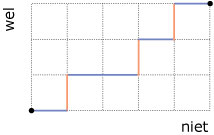
Hier zie je een rooster van 5 bij 3. Er zijn in elk roosterpunt twee keuzes: je gaat richting "wel" of richting "niet".
Je kunt het aantal routes zonder omwegen tellen van het punt linksonder naar dat rechtsboven.
Elke route (zonder omwegen en vanaf linksonder) bestaat uit een rijtje als NWNNWNWN, 3 keer "wel" en 5 keer "niet".

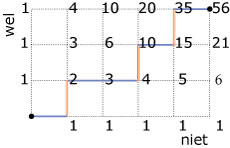
Het aantal routes naar een punt is telkens het aantal routes dat in het punt eronder en dat er links naast bij elkaar komt opgeteld.
Het is de som van de routes van de twee voorgangers.
Je kunt dat in de figuur gemakkelijk natellen als je bedenkt dat je (kortste routes) alleen naar rechts en omhoog kunt bewegen over de roosterlijnen.
Dit telpatroon staat bekend als de driehoek van Pascal.
(Meer hierover bij "Totaalbeeld".)

Je kunt het aantal rijtjes NWNNWNWN ook tellen met behulp van combinaties.
Je moet dan 3 uit de 8 posities kiezen om een W neer te zetten, daarbij speelt volgorde binnen het groepje van 3 W's geen rol. (En binnen het groepje N'en ook niet.)
Je vind dan $\left(\begin{array}{c}8\\ 3\end{array}\right)$ = 56 mogelijkheden.