Voorbeeld
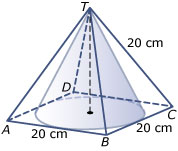
In de regelmatige vierzijdige piramide `T.ABCD` past precies een kegel met top `T`.
De grondcirkel van die kegel past precies in vierkant `ABCD`.
Hoeveel % van de inhoud van de piramide zit buiten de kegel?
Antwoord
In Voorbeeld 2 is de hoogte van de piramide (en dus ook de kegel) berekend: `h = sqrt(200)`.
Ook vind je daar dat de inhoud van de piramide `200 sqrt(200) ~~ 1886` cm3 is.
De kegel heeft als grondvlak een cirkel met straal `10`. De oppervlakte van het grondvlak is `G = pi * 10^2 = 100pi`.
De inhoud van de kegel is `1/3 * G * h = 1/3 * 100pi * sqrt(200) ~~ 1481` cm3.
Omdat `1481/1886 ~~ 0,79` zit 79% van de inhoud van de piramide binnen de kegel. En 21% zit er dus buiten.
