
Waar gaat het over?
Het woord 'gulden' hangt samen met het feit dat in de Renaissance de verhouding
die ontstaat na het aanbrengen van de gulden snede als volmaakt geldt.
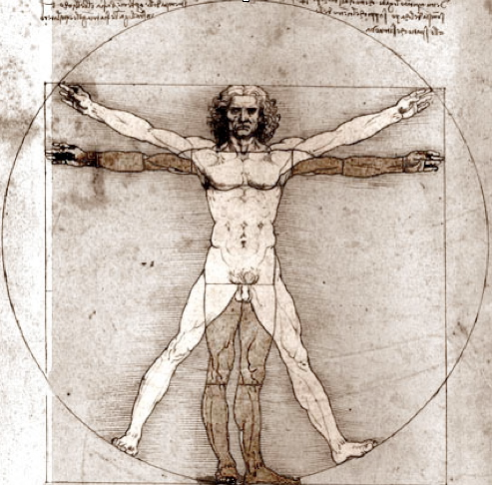
Leonardo da Vinci tekent het ideale menselijk lichaam gebaseerd op de verhouding
1:1,618 van de gulden snede.
Onder de gulden snede van een lijnstuk versta je een zodanige
verdeling van een lijnstuk in twee delen, dat het grootste deel middelevenredig
is tussen het kleinste deel en de gehele lijnstuk. Dit wil zeggen dat de volgende
evenredigheid geldt:
grootste deel : kleinste deel = geheel : grootste deel
Hoe werkt het?
Is het grootste deel van het lijnstuk a en het kleinste deel b, dan is de verhouding: a : b = (a+b) : a
De verhouding a/b wordt het gulden getal genoemd en aangeduid met de Griekse letter φ ≈ 1,62.
Wie en wanneer?
Euclides (300 v. Chr.) geeft in zijn "Elementen" op twee plaatsen een constructie voor het verdelen van een lijnstuk volgens de gulden snede.
Laat C het punt zijn dat AB verdeelt volgens de Gulden Snede.
Als BC = 1 en AC = x dan is AB = x+1.
Uit AB : AC = AC : BC, volgt
`(x+1)/x=x/1`
zodat `x^2-x-1=0`
De positieve wortel hiervan is `x=(1+sqrt5)/2` ≈ 1,618.
Meer over Gulden Snede:
> In Wikipedia (NL)
> The Golden Mean
> Fibonacci numbers
Op school:
Hier komen verwijzingen naar schoolwiskunde.
In bedrijf:
Beroepen waar de Gulden Snede wordt gebruikt.