Beroemde wiskundigen

Jean Victor Poncelet werd op 1 juli 1788 geboren in Metz en overleed in Parijs op 22 december 1867. Hij kwam uit een gegoede familie en was al snel betrokken bij het leger, zoals gebruikelijk in die tijd. Hij zat op de beroemde École Polytechnique in Parijs, waar hij onder meer les kreeg van Gaspard Monge, de grondlegger van de beschrijvende meetkunde. In het leger werd hij al snel luitenant van de ingenieurs en als zodanig ging hij mee op de dramatische tocht van Napoleon naar Rusland in 1812. Hij werd voor dood achtergelaten op het slagveld in Krasnoy, niet ver van Smolensk, na de ongelijke strijd waar 7000 koude, uitgehongerde fransen slag moesten leveren met 25000 uitgeruste russen. Het was er zo koud dat zelfs het kwik in de thermometers bevroor (-39°C). Hij kwam in een ziekenhuis in Saratov terecht waar hij gevangen bleef tot de overgave van Napoleon was getekend en het verdrag van Parijs werd gesloten (30 mei 1814). Toen kon hij terug naar Metz, waar hij in het volgende voorjaar goed herstelde van de ontberingen en zijn in Rusland bedachte wiskunde verder ontwikkelde. Hij kon namelijk in de gevangenis in Saratov niet veel anders doen dan de wiskunde die hij in de École Polythechnique had opgedaan onder Monge weer oppakken. Hij ontwikkelde daar de eerste ideeën van de projectieve meetkunde en is bekend als één van de grondleggers van die tak van de meetkunde.

» De tijd van Poncelet
» Over Poncelet
» Werk van Poncelet

Links naar ander(stalig)e sites:
» Over Poncelet

De tijd van Poncelet

Het is de tijd van de Franse revolutie. In West-Europa een tijd van leger, oorlogsvoering, maar ook van ontwikkeling. Daarbij speelden zo rond 1800, vooral Franse wiskundigen, zoals Lagrange (1736 - 1813), Legrendre (1752 - 1833), Laplace (1749 - 1827), Monge (1746 - 1818), Galois (1811 - 1832), Cauchy (1789 - 1857) en Gergonne (1771 - 1859), niet te vergeten, een grote rol.
Vele van die wiskundigen waren ook op de een of andere wijze betrokken bij het militaire gebeuren van die tijd. Zo speelde bijvoorbeeld Gaspard Monge een rol bij de opleiding van militaire ingenieurs. Wiskundig gezien hield hij zich vooral bezig met beschrijvende meetkunde, een in de techniek belangrijke, zich snel ontwikkelende tak van de wiskunde, die door middel van orthogonale aanzichten probeert waarheids(dus afmetings-)getrouwe afbeeldingen van objecten te (re)construeren. Poncelet was een leerling van Monge, vandaar ook zijn interessegebied. Het eind van de 18e eeuw was echter niet een gunstige tijd voor de meetkunde. Men was vooral bezig met de ontwikkeling van de calculus, de algebra en de getaltheorie.

Over Poncelet

Poncelet was de grondlegger van de projectieve meetkunde, een tak van de wiskunde waarin in de 15e eeuw in het bijzonder door Desargues al successen waren geboekt. De tijd van Poncelet is een tijd waarin de absoluutheid van de meetkunde van Euclides aan de orde was. Die 'absolute' meetkunde werd tot die tijd als enige mogelijkheid voor de vlakke meetkunde gezien. De pogingen in die tijd om het zogenaamde parallellenpostulaat van Euclides te bewijzen uit de andere vier postulaten leidde tot verrassende resultaten. Voor het eerst in 2000 jaar was men weer ontdekkend met de meetkunde bezig. In de negentiende eeuw zijn er dientengevolge verschillende meetkunden ontstaan, waarvan een aantal niet overeenkwam met de resultaten van die van Euclides.
Die zogenoemde niet-euclidische meetkunden, met voortrekkers als Bolyai en Lobashevski (en Gauss), werden in die tijd ontwikkeld en toegepast in onder meer de relativiteitstheorie van Einstein, in het begin van de twintigste eeuw. Poncelet hield zich met één van die bijzondere meetkunden bezig, een zuiver synthetische benadering van de meetkunde van de (centrale) projecties.
Naarmate zijn resultaten echter steeds verder kwamen af te staan van de ontwikkelingen in die tijd, die vooral gericht waren op de verdere ontwikkeling en toepassing van de algebra in de meetkunde, in gang gezet door Descartes, kreeg hij steeds meer conflicten met Gergonne en Cauchy en trok hij zich meer en meer terug in zijn oorspronkelijke aandachtsgebied, het construeren van machines.
Van 1825 tot 1835 was hij professor in de mechanica aan de école d'Application in Metz. Hij paste daar wiskunde bijvoorbeeld toe op de verbetering van turbines en waterraderen.

Chasles (1793-1880) nam zijn werk in de projectieve meetkunde over en breidde dit uit tot de moderne projectieve meetkunde. Sommige bronnen noemen Chasles dan ook wel de aartsvader van de projectieve meetkunde in plaats van Poncelet.

Werk van Poncelet

Poncelet heeft verschillende theorema's gepubliceerd in de jaren 1817 tot 1832 en een opmerkelijk boek. Veel van zijn resultaten vielen in die tijd niet goed. Het was de tijd van de analytische meetkunde en de veralgebraïsering. Het was voor Poncelet moeilijk om met zijn synthetische benadering door te dringen tot publicatie van zijn werk in bijvoorbeeld de "Annales des mathématique et appliquées", een toonaangevend wiskundig tijdschrift, zeker toen zo’n belangrijke figuur als Gergonne daar aan de touwtjes trok. Niet al zijn resultaten werden echter door Gergonne betwist en gelukkig publiceerde die er enkele in de "Annales...".

De wiskunde van Poncelet betreft, zoals gezegd, vooral meetkundige resultaten, zoals bijvoorbeeld:

Het porisme.
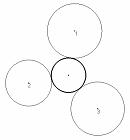
Het gaat om een bewering die nu bekend staat als het porisme van Poncelet. (Uit het Grieks vertaald betekent een porisme een indrukwekkend ding, een probleem dat of niet kan worden opgelost of oneindig veel oplossingen heeft) Het porisme van Poncelet betoogt het volgende: Neem twee concentrische kegelsneden (ellipsen, bijvoorbeeld, zie figuur), kies op de buitenste een punt P₁, construeer vervolgens door P₁ de raaklijn aan de binnenste; die raaklijn snijdt de buitenste in P₂. Construeer van P₂ uit weer een raaklijn aan de binnenste, dat levert P₃ op op de buitenste, enz.
Het porisme zegt nu: Als die constructie sluit, dat wil zeggen weer in P₁ terugkomt, dus zodat P_n = P₁, dan zal dat 'sluiten' onafhankelijk zijn van de startpositie van P₁.
Het tweede resultaat, uit 1818, stelt vast dat het aantal gemeenschappelijke raaklijnen aan twee krommen met respectievelijk graad m en k in het algemeen en op zijn hoogst mk(m – 1)(k – 1) is. Dus twee cirkels (m = 2 en k = 2) hebben op zijn hoogst 4 gemeenschappelijke raaklijnen.
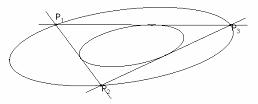
De derde was een nieuwe oplossing van het probleem dat het eerst door Apollonius van Perga (rond 200 v. Chr.), de beroemde Griekse meetkundige, werd geformuleerd, namelijk de constructie van een cirkel die raakt aan drie gegeven cirkels.
Zijn belangrijkste publicatie was het boek "Traité des propriétés projectives des figures" in 1822 wat een studie is welke eigenschappen van figuren onveranderlijk blijven bij (centrale) projectie. Dit werk bevat fundamentele ideeën van de projectieve meetkunde zoals de dubbelverhouding, perspectiviteit, involutie en de oneigenlijke punten. Bij het schrijven van dit werk zat bij Poncelet ook zeker een element van zending voor de zuivere kant van de wiskunde en het wiskundig redeneren. Hij hoopte dat de jeugd daardoor zou afblijven van wereldse geneugten als geld, bijvoorbeeld. Hij vond dat Frankrijk in die tijd in een moreel moeras zat.
In 1829 beschreef hij tenslotte in een artikel de theorie van de pool en poollijn met betrekking tot krommen van een hogere graad dan 2.

Verder was Poncelet een aanhanger van het principe van continuïteit, dat hij nodig had om zijn oneigenlijke punten en oneigenlijk rechte te kunnen verantwoorden. Het principe van continuïteit zegt in dit geval: twee lijnen snijden elkaar altijd, behalve als ze evenwijdig zijn, maar de verandering van niet-evenwijdig naar evenwijdig is een zo kleine verandering dat de eigenschap 'snijden' daardoor niet zal veranderen. Aan dat principe kleefden natuurlijk nogal wat bezwaren die Poncelet in zijn "Traité ..." ook wel voorzag, maar niettemin vond hij het gerechtvaardigd dit principe te gebruiken om zijn wiskunde verder te ontwikkelen. Het principe van continuïteit speelt bij die ontwikkeling voortdurend een rol.

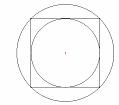
Cauchy was hier niet gelukkig mee, hij vond dit principe niet goed, omdat teveel vertrouwen in dit principe kan leiden tot duidelijke fouten. Er zijn nu eenmaal formules, bijv. over lengte, opp. en inhoud, die alleen waar zijn binnen bepaalde grenzen, en waarbij je die grenzen zeker niet moet overschrijden. Wel was hij, en zijn commissie, zeer gecharmeerd van de theorie van de ideale koorde van kegelsneden.
Die had Poncelet nodig voor de volgende redenering: Het sluitingsvraagstuk, het porisme, geldt duidelijk voor bijvoorbeeld een cirkel met daarin een vierkant, een sluitend figuur dus. In dat vierkant is weer een ingeschreven cirkel te tekenen. Die cirkels zijn concentrisch. Het vierkant kun je draaien, zonder dat er iets aan de configuratie verandert. Dus voor dit geval geldt het porisme wel.
Maar hoe zit het nu bij twee willekeurige kegelsneden? Het zou mooi zijn als je de kegelsneden kunt projecteren naar twee cirkels, waarvoor je het porisme wel zou kunnen bewijzen, wetende dat het dan ook in het algemeen geldt. Dat nu was de opdracht van Poncelet, een lastig probleem. En daar had hij zijn ideale koorde, oneigenlijke punten en oneigenlijke rechte voor nodig.

Math4all auteur: Hans Krabbendam