Liu Hui ( , ongeveer 220 - ongeveer 280 na Chr.) was een Chinees wiskundige, die leefde in de "periode van de drie koninkrijken" in het koninkrijk Wei. Hij is bekend geworden door zijn commentaren op het boek "Jiuzhang Suanshu" ( ; "Negen hoofdstukken over de kunst van de wiskunde") uit 263 na Chr. In dit boek was toen door verder onbekende schrijvers de Chinese wiskunde van de voorgaande eeuwen opgetekend.
Hij voegde onderliggende principes van diverse berekeningen toe. Hij benaderde π door middel van regelmatige veelhoeken binnen een cirkel; zijn beste benadering was 3,1416. Kennelijk was hij met limietprocessen (vergelijkbaar met de uitputtingsmethode van Eudoxus) vertrouwd en kende hij het begrip "limiet". In een toevoeging aan zijn commentaar op hoofdstuk 9 van de "Jiuzhang Suanshu" gebruikte hij de Gougu-stelling (die wij kennen als de stelling van Pythagoras) om landmeetkundige problemen zoals de hoogte van en afstanden tot bepaalde objecten te berekenen als ze niet rechtstreeks konden worden gemeten. Deze toevoeging groeide uiteindelijk uit tot een afzonderlijk boekje "Haidao Suanjing" ("Wiskundig handboek van het Zee-eiland"), zo genoemd naar het eerste probleem erin. Over Liu Hui's leven is verder niets bekend...
» De tijd van Liu Hui |
 |
|
Links naar anderstalige sites: » Over Liu Hui » Liu Hiu's afleidingen van de inhoud van lichamen |
De tijd van Liu Hui
EÉn van de beroemdste tijdperken uit de Chinese geschiedenis is dat van de Han-dynastie.
Het is de periode van 200 v.Chr. tot 220 na Chr. waarin China werd geregeerd door keizers uit de familie Han en waarin het tot grote bloei kwam. De Grote Muur werd in die periode gebouwd. En in die periode werd het boek "Jiuzhang Suanshu" ("Negen hoofdstukken over de kunst van de wiskunde") samengesteld, waarschijnlijk om ambtenaren te helpen, bijvoorbeeld bij berekeningen rond grondbezit.
Aan het einde van de beroemde Han-dynastie was de macht van de keizer vrijwel volledig overgenomen door de belangrijkste generaal Ts'ao Ts'ao. In 220 na Chr. droeg de laatste keizer van de familie Han de macht over aan de zoon van Ts'ao Ts'ao, die de eerste keizer van de Wei-dynastie werd. Maar vrijwel meteen riepen twee andere generaals eigen koninkrijken uit: het Shu Han koninkrijk en het Wu koninkrijk. Deze "periode van de drie koninkrijken" duurde ongeveer 60 jaar, dus tot 280.
» Meer over de periode der drie koninkrijken in Wikipedia
Liu Hui leefde in de periode van de drie koninkrijken in het koninkrijk Wei dat was gelegen in de huidige Shansi-provincie in het noordelijke deel van centraal China. Het was een tijdperk van constante oorlogen tussen de drie koninkrijken om de macht over heel China. In 263 slaagde Wei er in om Shu Han te veroveren, maar twee jaar later werd de Wei-dynastie afgezet en ontstond de westelijke Tsjin-dynastie. Uiteindelijk viel in 280 ook het koninkrijk Wu ten prooi aan de Tsjin-keizer.
Of Liu Hui van al deze strubbelingen veel heeft gemerkt is maar zeer de vraag. Een aantal zaken veranderde echter fundamenteel: het gebruik uit de Han-periode om alleen tot de ambtenarij diegenen toe te laten die het beste hun examens deden verminderde ten gunste van baantjes toeschuiven op grond van afkomst en/of kennissenkring. Het Confucianisme (als filosofisch kader voor de ambtenaren en de heersende klasse) verloor veel van zijn kracht (want het had de Han-dynastie niet voor ineenstorten kunnen behoeden). Allerlei filosofische stromingen (zoals het Taoïsme) wonnen aan invloed en veranderden de filosofie achter het handelen van de machthebbers en het staatsapparaat.
Dat over Liu Hui's leven niets bekend is komt waarschijnlijk omdat het beroep wiskundige in die tijd niet bestond, hoewel wiskunde zelf wel als heel belangrijk werd beschouwd. Bijna alle wiskundige werk werd door anonieme ambtenaren gedaan, gewoon in het kader van de rekenmethoden die ze nodig hadden in hun dagelijkse praktijk.
Overzicht van de Oud-Chinese wiskunde
De cultuur van het Oude China is in betrekkelijk isolement ontstaan: tussen China en de oude Babylonische en Perzische en Indische Rijken liggen hoge bergmassieven (de Himalaya), aan de noordkant ligt de Gobi-woestijn en aan de oostkant ligt de zee. Ook de wiskunde in het Oude China lijkt zich onafhankelijk van die in andere culturen te hebben ontwikkeld.
De Chinese wiskunde ontstond net als die in het Oude Egypte en in Babylonië vanuit de rekenbehoeften van het ambtelijk apparaat en de handel. Voor een theoretische opbouw via basisaannames en stellingen met bewijzen vanuit die basisaannames was geen noodzaak en geen interesse. De wiskunde was net als de Chinese taal zeer compact en sterk probleem gestuurd. Problemen rond de kalender, handel, land meten, bouwkunde en belastingen bepaalden welke wiskunde werd ontworpen en welke niet.
Het belangrijkste feit was wel de invoering van zogenaamde telborden in de vierde eeuw voor Chr.
Zo'n telbord had de vorm van een dambord van 10 rijen bij 10 kolommen. Elke rij stelde een getal voor met de eenheden links, de tientallen daarnaast, dan de honderdtallen, enzovoorts. Zo ontstond op volkomen natuurlijke wijze het eerste positiestelsel voor getallen. De cijfers van een getal werden gemaakt met behulp van bamboestokjes:
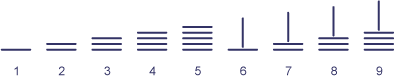
Om verwarring te voorkomen legden de Chinezen de cijfers voor de tientallen iets anders, namelijk:
Die voor de honderdtallen waren weer net als die voor de eenheden, cijfers voor de duizendtallen net als die voor de tientallen en zo steeds maar weer om en om. Het getal 12345 werd dan:
en bijvoorbeeld 16072 werd:
Je ziet dat voor de "nul" gewoon een leeg vak werd gebruikt: een nul als symbool bestond in die tijd niet.
Deze Chinese telbord-getallen ontstonden uit het gebruik van het telbord, maar werden later ook gebruikt als notatie voor getallen in geschreven teksten. Deze notatie maakt een opmerkelijke ontwikkeling van de wiskunde in China in de periode van 400 v.Chr. tot 200 na Chr. die werd vastgelegd in een praktisch handboek: "Jiuzhang Suanshu" ("De negen hoofdstukken over de kunst van de wiskunde").
De negen hoofdstukken over de kunst van de wiskunde
Dit is een praktisch handboek voor wiskunde uit het tijdperk van de Han-dynastie van 200 voor tot 220 na Chr. Het bestaat uit 246 oplossingen van gestelde problemen en was bestemt voor de ambtenaren van het Chinese Rijk. Het was bedoeld om ze te laten zien hoe alledaagse rekenproblemen op het gebied van bouwkunde, landmeetkunde, weg- en waterbouwkunde, handel en belastingen konden worden aangepakt. Het boek is fundamenteel geweest voor de ontwikkeling van de wiskunde in het Oude China (het is in dat opzicht vergelijkbaar met "De Elementen" van Euklides voor de Oud-Griekse wiskunde) en ook voor de organisatie van het Rijk. De wiskundigen van latere perioden (waaronder Liu Hui) geven vooral commentaren en aanvullingen op dit boek.
Hoewel "Jiuzhang Suanshu" geen strikte opbouw kent vanuit uitgangspunten met stellingen die van daaruit werden bewezen (zoals "De Elementen" van Euklides die wel kende), worden alle oplossingsmethoden vanaf de tijd van Liu Hui zorgvuldig gemotiveerd. Ook de Chinese schrijvers van dit boek was het er veel aan gelegen om hun werkwijzen te verantwoorden.
"Jiuzhang Suanshu" () bestaat uiteraard uit negen hoofdstukken:
Hoofdstuk 1: Landmeten
Dit hoofdstuk bestaat uit 38 problemen op het gebied van de landmeetkunde. Eerst gaat het over oppervlakte berekening, daarna over het optellen, aftrekken, vermenigvuldigen en delen van breuken. Euclides' rekenmethode voor het bepalen van een grootste gemene deler van twee getallen wordt beschreven. Daarna volgen er opnieuw oppervlakteberekeningen (die overigens geen gebruik maken van het materiaal over het rekenen met breuken): de oppervlakte van rechthoek, driehoek, cirkel en trapezium worden besproken. In vraagstuk 32 wordt een benadering voor π gegeven die behoorlijk nauwkeurig is.
Hoofdstuk 2: Gierst en rijst
In dit hoofdstuk staan 46 oplossingen van problemen rond de verdeling van goederen. Met name de wisselkoersen tussen zo'n twintig soorten granen, bonen en zaden zijn er te vinden. De wiskunde erin gaat daarom over verhoudingen en percentages. Veel van de gestelde problemen zijn niet erg realistisch en lijken vooral bedoeld om het rekenen met verhoudingen te oefenen.
Hoofdstuk 3: Verdelen naar verhouding
Hierin worden 20 problemen behandeld over (opnieuw) verhoudingen. Nu gaat het om uitbetalingen aan ambtenaren van verschillende rang. Recht evenredig en omgekeerd evenredig komen als begrippen voorbij. Verder worden rekenkundige en meetkundige rijen gebruikt.
Hoofdstuk 4: Verkorte breedte
De naam van dit hoofdstuk is afgeleid uit de eerste 11 problemen die gaan over de lengte van een rechthoek waarvan de breedte steeds korter wordt, maar de oppervlakte hetzelfde blijft. Daarbij wordt gewerkt met stambreuken. Het gaat om vraagstukken als:
| Als de breedte van een rechthoek 1 + 1/2 + 1/3 + 1/4 + ... 1/12 is en de oppervlakte is 1, hoe groot is dan de lengte? |
Daarna gaat het om worteltrekken en het trekken van derdemachtswortels. Zelfs komen het limietbegrip en de notie van "infinitesimaal klein" om de hoek kijken.
Hoofdstuk 5: Weg- en waterbouwkunde
Hier vind je 28 problemen rond het bouwen van kanalen, sloten, dijken, enz. Er komen inhoudsberekeningen van prisma, piramide, tetraëder, cilinder en afgeknotte varianten daarvan voor. Liu Hui voegde er een bespreking van zijn versie van de uitputtingsmethode aan toe waarmee hij de juiste formule voor de inhoud van een piramide kon afleiden.
Hoofdstuk 6: Eerlijke verdeling van goederen
In dit hoofdstuk gaat het weer over verhouding en evenredigheid. Deze komen aan de orde in een gevarieerde verzameling van opgeloste problemen over belastingen, verdelingen, voortbeweging, enz. Een paar voorbeelden:
Probleem 12:
| Een goede hardloper loopt 100 passen tegen elke 60 passen van een slechte loper.
De slechte loper heeft 100 passen gelopen als de goede loper de achtervolging inzet. Na hoeveel passen heeft de goede loper de slechte loper ingehaald? [Antwoord: 250 passen] |
Probleem 26:
| Een bekken wordt gevuld door vijf kanalen. Open je het eerste kanaal dan loopt het bekken in 1/3 dag vol; open je het tweede kanaal dan loopt het in 1 dag vol; bij het derde kanaal is dat 2 1/2 dag; bij het vierde 3 dagen en bij het vijfde 5 dagen. In hoeveel dagen loopt het bekken vol als alle kanalen tegelijk worden geopend? [Antwoord: 15/74 dag] |
Hoofdstuk 7: Overschot en tekort
In dit hoofdstuk worden problemen opgelost die leiden tot lineaire vergelijkingen (in de moderne notatie). Bijvoorbeeld:
Probleem 1:
| Een bepaald artikel wordt door meerdere personen samen aangeschaft. Als ze elk 8 munten inzetten, hebben ze 3 munten teveel. Zetten ze elk 7 munten in, hebben ze 4 munten te weinig. Met hoeveel personen zijn ze en hoeveel kost het artikel? [Antwoord: 7 personen en 53 munten] |
Probleem 18:
| Er zijn twee stapels munten: 9 gouden munten en 11 zilveren munten. Beide stapels zijn even zwaar. Uit elke stapel wordt ÉÉn munt gehaald en op de andere stapel gelegd. Nu is de stapel met merendeels gouden munten 13 eenheden lichter dan de andere stapel. Hoeveel weegt een gouden munt en hoeveel een zilveren? [Antwoord: een gouden munt is 91/4 eenheden, een zilveren munt is 819/44 eenheden] |
Hoofdstuk 8: Berekeningen met vierkante tabellen
Nu gaat het over 18 oplossingen van vraagstukken waarbij stelsels vergelijkingen worden aangepakt met behulp van een soort van matrixrekening. In moderne terminologie wordt de toegevoegde coëfficiëntenmatrix van het stelsel door eliminatie 'geveegd' tot een vorm waarin je de oplossingen kunt vinden. het enige verschil met de moderne werkwijze is dat de eliminatie in kolommen gebeurt en niet in rijen. Er worden negatieve getallen bij gebruikt en ook het rekenen met dergelijke negatieve getallen wordt besproken.
Hoofdstuk 9: Rechthoekige driehoeken
In dit laatste hoofdstuk staan 24 problemen betreffende rechthoekige driehoeken. Vaak wordt daarbij gebruik gemaakt van de Gougu-stelling (die wij de stelling van Pythagoras noemen) en van gelijkvormigheid. Een voorbeeld is probleem 20:
| Een stad is omgeven door een volkomen vierkante muur. (Zoals in China in die tijd gebruikelijk was.) Er is een poort in het midden van elke zijde. Twintig passen buiten de Noordelijke poort bevindt zich een boom. Als je de stad vauit de Zuidelijke poort verlaat en je loopt 14 passen naar het Zuiden en 1775 passen naar het Westen, kun je die boom net zien. Wat zijn de afmetingen van de muur van deze stad? [Antwoord: 250 passen; maak een schets en ontdek daarin twee gelijkvormige driehoeken, noem de zijde van het vierkant x en los de vergelijking op die ontstaat uit de gelijkvormigheid] |
Je vindt het antwoord op dit probleem door een kwadratische vergelijking op te lossen. In dit hoofdstuk komen die voor het eerst aan bod. Ze worden met behulp van meetkundige methoden opgelost (aanvullen van een onvolledig vierkant tot een volledig vierkant waarvan de oppervlakte bekend is). Bij de oplossing van probleem 20 is dat goed te zien.
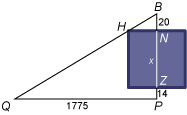
Het midden van de Noordelijk poort is punt N, dat van de Zuidelijke poort Z. Bij B staat de boom, je loopt eerst naar P en dan naar Q. De afmetingen vind je in de figuur, de lengte en de breedte van de stad noem je x.
Omdat ΔBNH gelijkvormig is met ΔBPQ is:
En daaruit volgt: x2 + 34x = 71000.
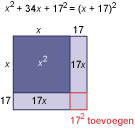
Deze vergelijking is met behulp van de figuur hiernaast te herschrijven tot:
(x + 17)2 = 71289
Door worteltrekken vind je: x + 17 = 267.
Dus x = 250.
Liu Hui's bijdrage aan de wiskunde
Liu Hui's commentaren op "Jiuzhang Suanshu" zijn volledig in de tekst geïntegreerd. De belangrijkste aanvulling is wel dat hij de principes toevoegde waarop de berekeningen zijn gebaseerd: "Jiuzhang Suanshu" was voordat Liu Hui er zijn commentaar invoegde vooral een verzameling recepten van hoe je bij bepaalde problemen moest rekenen, hij gaf verklaringen voor de gebruikte methodes. Niet in de vorm van een bewijs zoals wij dat nu kennen, maar meer als een soort van uitleg waarom de verschillende rekenstappen geldig zijn.
Een voorbeeld is de introductie van de Gougu-stelling (de stelling van Pythagoras) in de "Jiuzhang Suanshu" in de eerste drie problemen van hoofdstuk 9:
| 1. Als het korte been (van een rechthoekige driehoek) 3 eenheden is en het langere been is 4 eenheden, hoeveel is dan de hypothenusa? 2. Als de hypothenusa 5 eenheden is en het korte been is 3 eenheden, hoe lang is dan het langere been? 3. Als het langere been 4 eenheden is en de hypothenusa is 5 eenheden, hoeveel is dan het korte been? [Antwoord op 1: Vermenigvuldig het korte been met zichzelf en het langere been met zichzelf en tel beide resultaten op. Trek uit de uitkomst de wortel. Op de andere twee problemen worden vergelijkbare antwoorden gegeven, maar nu met afttrekkingen.] |
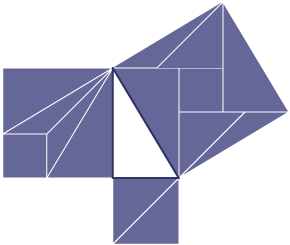Liu Hui geeft een meetkundige uitleg door vast te stellen dat de vermenigvuldiging van een been met zichzelf (de oppervlakte van) een vierkant op zo'n been oplevert. De vierkanten van het korte en het langere been zijn op te knippen en de stukken bedekken dan precies het vierkant op de hypoyhenusa. (Zie figuur)
Liu Hui verbetert ook een aantal benaderingsmethoden die in de "Jiuzhang Suanshu" worden gebruikt, het lijkt er zelfs op dat hij begrippen die te maken hebben met de beginselen van de differentiaal- en integraalrekening al begint de doorzien. Een voorbeeld hiervan is zijn bijdrage aan de benadering van π zoals die is te vinden in het eerste hoofdstuk van de "Jiuzhang Suanshu".
De waarde van π wordt daar benaderd door in een cirkel met straal r en middelpunt M een regelmatige veelhoek te tekenen en dan de omtrek ervan door de diameter van de cirkel te delen. (Neem je r = 1 dan is de halve omtrek een benadering van π.)
Hoe groter het aantal zijden van de veelhoek, hoe beter de benadering, zo begrijpt Liu Hui. Hij verzint een procedure waarbij het aantal zijden van de veelhoek steeds wordt verdubbeld, startend met een zeshoek (n = 1). De omtrek van die zeshoek is 6r en de diameter van de cirkel 2r, dus dat geeft π ≈ 3.
Bij n = 2 heb je dan een twaalfhoek, bij n = 3 een 24-hoek, etc.
Bij n heb je een 3 · 2n-hoek.
Noem de lengte van een zijde die veelhoek pn.
Bij n + 1 heb je een 3 · 2n + 1-hoek.
De lengte van een zijde van die veelhoek is met de Gougu-stelling af te leiden uit pn.
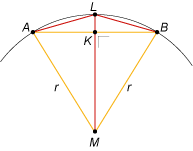
Zie figuur: AB = pn de zijde van de veelhoek bij n, AL = pn + 1 de zijde van de veelhoek bij n + 1.
Uit MA = r, ML = r en AK = 0,5pn is af te leiden dat
Met behulp van deze recursieformule kun je nu de omtrek van de veelhoek bij n + 1 uit die bij n afleiden en zo beginnend bij n = 1 en uitgaand van r = 1 benaderingen van π vinden.
Als bij n = 10 vind je π ≈ 3,141592104, een benadering waarvan de eerste zes decimalen juist zijn! Liu Hui kent uiteraard de hierboven gebruikte algebraïsche notatie niet, hij heeft zijn eigen schrijfwijzen, maar gebruikt in essentie de geschetste methode. Daarmee laat hij zien het begrip "limiet van een rij" te begrijpen.
Bovendien laat Liu Hui zien, dat je de oppervlakte van de cirkel kunt krijgen door de halve diameter en de halve omtrek te vermenigvuldigen.
Liu Hui's aanvullingen van hoofdstuk 9 van de "Jiuzhang Suanshu" zijn later tot een afzonderlijk boekje omgevormd. Het kreeg de naam "Haidao Suanjing" ("Wiskundig handboek van het Zee-eiland") en bestaat uit negen opgeloste problemen waarbij de Gougu-stelling (de stelling van Pythagoras) wordt toegepast bij het berekenen van hoogtes van voorwerpen of afstanden tot voorwerpen die niet eenvoudig door meten te vinden zijn. Het eerste probleem bijvoorbeeld gaat over de hoogte van en de afstand tot een eiland in zee:
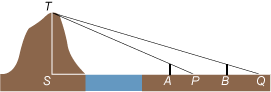
| Bij A en B staan twee palen van 5 pu hoog en 1000 pu uit elkaar. (1 pu is ongeveer 2 meter.)
Bereken de hoogte van de top van het eiland en de afstand van het eiland tot A. [Antwoord: de hoogte TS = 1255 pu en de afstand SA = 30750 pu.] |
Andere problemen in dit boekje gaan over de hoogte van een boom op een berghelling, de afstand tot een vierkant ommuurde stad, de diepte van een kloof, de hoogte van een toren die op een heuvel staat, de bredte van een rivier, de diepte van een vallei met een meer op de bodem van de vallei, de breedte van een kloof gezien vanaf een heuvel en de afmetingen van een stad gezien vanaf een berg.
Uit zijn geschriften komt naar voren dat Liu Hui een groot wiskundige is met een brede maatschappelijke belangstelling. Hij schrijft helder en put uit een groot aantal bronnen. Bescheiden is hij ook: hij kon de juiste berekening van de inhoud van een bol niet vinden en zei: "laten we dit probleem overlaten aan iemand die de waarheid kan vertellen".
Math4all