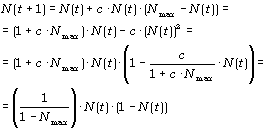Geremde groeimodel en chaos

Inhoud:

• Het logistisch groeimodel met stapgrootte 1
• Chaotische groei en vertakkende grenswaarden
• Het bifurcatiediagram en chaos

dN = N(t + 1) – N(t) = c · N(t) · (N_max – N(t))

Hierin in c een constante en stelt dN de verandering van N voor.
De grootte van de constante hangt af van de omstandigheden waaronder die cultuur bacteriën leeft. Door metingen kun je die constante bepalen. Excel kan voor verschillende waarden van c snel het model doorrekenen en die rekenresultaten kun je dan vergelijken met je meetwaarden.
Vaak is het handig om N_max = 1 te nemen en N op te vatten als een deel (een percentage) van N_max. Dat betekent dat N dan waarden tussen 0 en 1 zou moeten aannemen. Het bijbehorende logistische groeimodel is dan:

N(t + 1) = N(t) + c · N(t) · (1 – N(t))

Open nu (met de rechtermuisknop kun je downloaden en door te kiezen 'doel opslaan als...' opslaan onder een eigen naam) de werkmap

Model logistische groei en chaos.

N(t + 1) = N(t) + c · N(t) · (1 – N(t))

wordt weergegeven door N := N + c*N*(1 – N).
Dat betekent in woorden: 'de nieuwe waarde van N wordt de oude waarde van N plus c*N*(1 – N)'.
De modelformules t := t + 1 en N := N + c*N*(1 – N) worden gebruikt om de tabel met resultaten te berekenen. Dat is te zien door te klikken op de cellen A11 en A12 en B11 en B12:

• In A11 staat als Excel formule: =$E$3, hetgeen betekent dat deze cel de waarde van cel D3 krijgt, dat is de startwaarde voor de tijd.
• In A12 staat: =A11+$E$4, hetgeen betekent dat A12 de waarde van de cel erboven krijgt plus de stapgrootte (t  := t + 1). Deze formule is daarna gekopieerd naar een flink aantal volgende cellen onder A11, zodat je een mooie tabel krijgt. Omdat A11 geen dollartekens heeft, wordt bij het kopiëren steeds de celwaarde automatisch aangepast. Bijvoorbeeld in A14 komt: =A13+$E$4. Door de dollartekens verandert de verwijzing naar cel D4 niet.
• In B11 staat: =$E$5, dus cel B11 krijgt de startwaarde die in cel D5 staat.
• In B12 staat: =B11+$E$6*B11*(1–B11), de vertaling van N := N + c*N*(1 – N). Let ook nu op de plaatsing van de dollartekens. Deze laatste formule wordt dan gekopieerd naar alle volgende cellen onder B12 (net zoveel als in de tijdtabel).

• Experimenteer even met het groeimodel door de startwaarden te veranderen. Kijk wat er met de grafiek en de tabel gebeurt.
• Je ziet, dat als c > 1 de groei even 'doorschiet' boven het veronderstelde maximum, maar dan toch terugschommelt naar dit maximum.
• Als c > 2 dan gebeurt er al iets vreemds: er lijkt een soort van blijvende periodieke sprongen tussen twee waarden te ontstaan.
• Laat c maar eens verder oplopen, maar niet te snel. Kom je in de buurt van c = 3 dan onstaat er een chaotisch springend patroon.
• Als c > 3 dan 'explodeert' de groei.

Model logistische groei en chaos

Op blad 2 'Chaotische groei' is het logistisch groeimodel

N(t + 1) = N(t) + c · N(t) · (N_max – N(t))

omgeschreven tot:

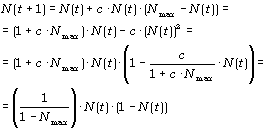
Je krijgt dan een rij getallen met voorschrift:

N(t + 1) = a · N(t) · (N_max – N(t))

Nu is N nog steeds een getal tussen 0 en 1, dus een deel van N_max = 1 en de groei verloopt bijna net zo als in het hiervoor beschreven model van logistische groei. Alleen komt de populatie uiteindelijk niet op 1 uit, maar wat lager.

Bekijk op het Excel-rekenblad wat er gebeurt als je a verandert.

• Als a = 2 ontstaat er iets wat heel erg lijkt op logistische groei: N nadert 0,5. Dus uiteindelijk wordt er een soort van grenswaarde bereikt.
• Als a > 3 wordt het gedrag van N op den duur nogal vreemd, er wordt geen vaste grenswaarde meer bereikt:
  • eerst gaat N uiteindelijk tussen twee grenswaarden heen en weer springen;
  • vervolgens als a in de buurt van de 3,5 komt gaat N tussen vier grenswaarden periodiek heen en weer bewegen;
  • en daarna als a tussen 3,6 en 4 wordt gekozen wordt het patroon heel erg chaotisch;
  • als a > 4 dan 'explodeert' de groei.

Bijvoorbeeld kun je op het lege rekenblad voor a lopend van 1, 1,1, 1,2, 1,3, enzovoorts tot en met 4 telkens doorrekenen tot aan N(2000). Vervolgens maak je een grafiek (spreidingsdiagram met horizontaal de waarden van a en verticaal de waarden voor N) waarin voor elk van de gekozen waarden van a de getallen N(1900), N(1901), N(1902), ..., N(2000) staan uitgezet.
Helaas is het in Excel nauwelijks mogelijk om dit echt nauwkeurig te doen, daarvoor zijn krachtiger programma's nodig. Maar de situaties die hierboven zijn beschreven worden wel zichtbaar. Er onstaat een diagram waarin je ziet dat vanaf a = 3 de grenswaarden zich steeds meer vertakken. Uiteindelijk zie je ook de zich steeds chaotischer vertakkende grenswaarden.

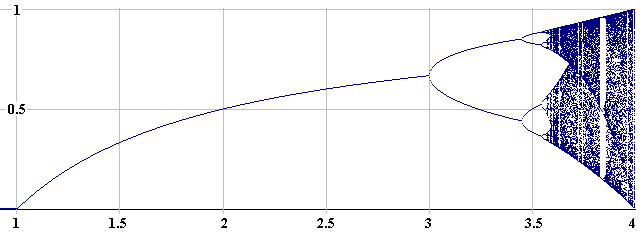
Dit heet een 'vertakkingsdiagram' of 'bifurcatiediagram'.
Het chaotische vertakken van de grenswaarden als a tussen 3,5 en 4 ligt, wordt zo nog duidelijker. Maar die chaos treedt niet voortdurend op, soms zijn er precies vier mogelijke grenswaarden, of precies acht. Verder heeft dit diagram eigenschappen die je ook bij fractalen tegenkomt: als je inzoomt op de grafiek dan hebben de details dezelfde vormen als het geheel.
Dat inzoomen kun je even proberen bij de applet hieronder waarin het bifurcatiediagram staat afgebeeld voor a vanaf 2,0 tot 4,0. Hij is gemaakt door de Japanner Takashi Kanamura en gevonden op het internet.

Sleep met de muis over het deel dat je wilt vergroten.

Je krijgt nu een beetje beeld van de eigenschappen van chaotische systemen:

• een hele kleine wijziging in de ranvoorwaarden (hier: een hele kleine verandering van de waarde van c) heeft hele grote gevolgen;
• die gevolgen zijn vaak nogal onvoorspelbaar;
• op grote schaal lijken dezelfde situaties zich af te spelen als tot in de kleinste details.