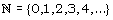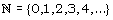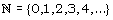Getallen om te tellen
Getallen zijn ontstaan door de behoefte om te tellen.
Eeuwenlang waren er dan ook geen andere dan 1,2,3,4,5,...
En vaak ging die rij niet erg ver door.
Andere getallen waren eeuwenlang onvoorstelbaar...
Inhoud:
De natuurlijke getallen
Deze natuurlijke getallen zijn de getallen waarmee je hebt leren tellen.
Eeuwenlang was dat genoeg: andere getallen bestonden niet.
Het getal 0 wat voor ons toch redelijk normaal is geworden, was overbodig: 0 was niks.
En voor iets dat er niet is heb je geen getal nodig!
Dat had veel te maken met de manier waarop getallen werden geschreven.
In het meest simpele systeem gewoon zoveel streepjes, krasjes, of andere vormpjes als het getal groot was.
Vaak was er dan voor 5 of 10 een afzonderlijk teken, net als 100 en soms zelfs 1000.
Tot in de dagen van de Grieken en de Romeinen waren dit de enige getallen.
De Grieken noteerden ze met behulp van de letters van hun alfabet,
ze hadden eigenlijk geen afzonderlijke tekens voor getallen.
De Romeinen gebruikten de bekende Romeinse getallen I, II, III, IV, V, VI, VII, VIII, IX, X, XI, etc.
Voor 50 gebruikten ze de L, voor honderd de C en voor duizend de M.
Pas veel later, toen er positiestelsels ontstonden en getallen werden opgebouwd uit cijfers
waarvan de positie de waarde bepaalde, werd de 0 bedacht.
Vanaf dat moment hoorde ook de 0 bij de natuurlijke getallen.
Het gebruik van een positiestelsel vergemakkelijkt het rekenen, vooral het vermenigvuldigen en het delen.
De verzameling van de natuurlijke getallen noteer je zo: