Simulaties en tellen met de TI-83/84
De TI-83/84 kan je behulpzaam zijn bij het bepalen van kansen. Hij kan simulaties van kansexperimenten uitvoeren en je helpen bij het tellen van mogelijkheden.
Loop eerst het practicum: 'Basistechnieken TI-83/84' door.
Inhoud
Simulaties
Het werpen met een dobbelsteen kun je simuleren met toevalsgetallen.
Bij de TI-83/84 vind je de 'randomizer' (toevalsgetallenmaker) door
- [MATH] te toetsen en dan naar PRB te gaan met de pijltjestoetsen en [ENTER]
- vervolgens 1: rand te kiezen en [ENTER]
- en dan op [ENTER] te blijven drukken.
Je krijgt zo toevalsgetallen tussen 0 en 1 (in tien decimalen).
Als je toevalsgetallen tussen 0 en 2 wilt, dan vermenigvuldig je ze met 2.
In het rekenscherm maak je: 2*rand en [ENTER].
Meestal heb je echter gehele toevalsgetallen nodig (bijvoorbeeld bij de dobbelsteen de getallen 1 t/m 6). Die kun je krijgen door 'integer' (geheel getal) te gebruiken. De integer-routine laat gewoon alle decimalen weg, dus van 0,78456... maakt deze routine gewoon 0: int(0,78456) = 0.
Maar int(2*0,78456) = int(1,56912) = 1.
Bij de TI-83 vind je 'integer' zo:
- [MATH] en naar NUM en dan [ENTER]
- kies 5: int(
- Als je nu int(2*rand) in het scherm zet en je geeft steeds [ENTER], dan krijg je de toevalsgetallen 0 en 1.
Probeer maar...
Het werpen met de dobbelsteen kun je nu simuleren door int(6*rand+1) in je rekenscherm te zetten en dan op [ENTER] te blijven drukken. In het plaatje hiernaast zie je dat gebeuren.
De TI-83/84 kent echter een routine om dit veel sneller te doen: randInt. Voor de simulatie van 10 keer werpen met een dobbelsteen ga je dan zo te werk:
- toets [MATH] en ga naar PRB en kies 5: randInt( en [ENTER]
- in het rekenvenster staat nu randInt( en je toetst er achter 1 [ , ] 6 [ , ] 10 [ ) ] en [ENTER]
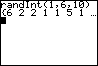Het resultaat zie je hiernaast.
De uitdrukking randInt(1,6,10) levert je gehele toevalsgetallen vanaf 1 t/m 6 en wel ineens 10 stuks. Met de pijltjestoets naar rechts krijg je ze alle tien te zien.
Werpen met dobbelstenen simuleren
Om met behulp van simulaties kansen te bepalen, moet je gemakkelijk kunnen tellen hoe vaak elk getal in je simulatie voor komt. Je zet daartoe je toevalsgetallen in een lijst.
Werpen met één dobbelsteen
Stel je voor dat je 100 keer met een dobbelsteen gooien wilt simuleren en zo de kans wilt bepalen op het gooien van een 5. Je doet dan het volgende:
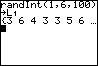
- Voer in je rekenscherm in: randInt(1,6,100)
- Vertel de rekenmachine vervolgens dat dit in lijst1 moet door er achter te tikken:
[STO>] [2nd] [ 1 ] en [ENTER]
- Alle toevalsgetallen staan nu in L1 (lijst 1), je kunt dat zien door te tikken:
[STAT] en naar 1: Edit... en [ENTER]
-
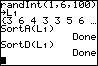Vervolgens kun je de lijst sorteren:
- van klein naar groot:
[STAT] en 2: SortA( en [ENTER] gevolgd door [2nd] [ 1 ] en [ENTER] (even wachten op de melding: Done)
- van groot naar klein m.b.v. SortD(
- In de gesorteerde lijst kun je gemakkelijk tellen hoe vaak de vijf voorkomt van de 100 'worpen'.
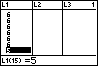In de lijst hiernaast is de eerste 5 nummer 15 van de lijst en de laatste 5 was nummer 29. Er kwam dus 15 keer een vijf voor. De kans op 5 was daarom in deze simulatie 0,15.
Nog eenvoudiger is het om eerst een staafdiagram te maken bij lijst L1 via StatPlot.
Hoe je een staafdiagram bij een lijst maakt vind je in het practicum 'Statistiek en de TI-83'.
Voer zelf zo'n simulatie uit.
Werpen met twee dobbelstenen
Als je bij het werpen met twee dobbelstenen de kans wilt bepalen op een bepaald aantal ogen dat op beide stenen samen boven komt te liggen, hebben niet alle mogelijkheden een gelijke waarschijnlijkheid.
Bij je simulatie moet je daarmee rekening houden: je simuleert elke dobbelsteen afzonderlijk en telt dan de uitkomsten bij elkaar. Een simulatie van 100 worpen met twee dobbelstenen gaat zo:
- Eerst voer je randInt(1,6,100) uit. Zet het resultaat in L1.
- Vervolgens voer je randInt(1,6,100) opnieuw uit. Zet het resultaat in L2.
- Vervolgens zet je in het rekenscherm: L1 + L2 en [ENTER].
- Het resultaat stop je vervolgens in L3.
- De simulatie van het werpen met twee dobbelstenen staat nu in L3. Deze lijst kun je sorteren en je kunt er een staafdiagram van maken. Met [TRACE] kun je nu gemakkelijk alle frequenties aflezen.
Voer zelf zo'n simulatie uit.
Dit is natuurlijk gemakkelijk uit te breiden tot het werpen met drie dobbelstenen, of vier munten, etc.
Zolang het maar niet over al te grote aantallen gaat...
Permutaties en combinaties
Het aantal permutaties van 6 elementen is het totale aantal mogelijke verwisselingen als alle 6 elementen verschillend van elkaar zijn.
Dat aantal permutaties is: 6 × 5 × 4 × 3 × 2 × 1 = 6!.
De TI-83 kan 6! op de volgende manier berekenen zonder de hele vermenigvuldiging in te tikken:
- voer eerst de 6 in
- toets daarna: [MATH] en ga naar PRB
- kies 4: ! en [ENTER]
Je ziet: 6! = 720.
Bij het aantal permutaties van bijvoorbeeld 4 uit 10 gaat het om de mogelijke keuzes van 4 onderling verschillende elementen uit 10 verschillende elementen, dus om 10 × 9 × 8 × 7 = 10! / 6!.
Je kunt dat met de TI-83 als volgt berekenen:
- voer de 10 in, toets daarna: [MATH] en ga naar PRB
- kies 2: nPr en voer 4 in
- sluit af met [ENTER] en je vindt: 5040
Ga na dat dit hetzelfde is als 10 × 9 × 8 × 7.
Het aantal combinaties van 4 uit 10 is 10! / 4! / 6!. Dit is het aantal mogelijke keuzes van 4 elementen uit 10 elementen die niet allemaal verschillend zijn, maar waarbij er twee groepen zijn: één van 4 onderling gelijke elementen en één van 6 andere, maar onderling gelijke elementen.
Met de TI-83/84 kun je het aantal combinaties van 4 uit 10 zo berekenen:
- voer de 10 in, toets daarna: [MATH] en ga naar PRB
- kies 3: nCr en voer de 4 in
- sluit af met [ENTER] en je vindt: 210
Ga na dat dit hetzelfde is als 10! / 4! / 6! en ook als 10! / (4! × 6!).
Wanneer je het aantal mogelijke keuzes moet berekenen uit 10 elementen waarbij een groep van 2 onderling gelijke, van 3 onderling gelijke en van 5 onderling gelijke elementen ontstaan, dan kun je sneller niet met nCr werken.
Dan bereken je: 10! / 2! / 3! / 5! of 10!/(2! × 3! × 5!)
Math4all