 Gebruik nu twee lijsten voor de tabel hierboven, bijvoorbeeld:
L1 vul je met schoenmaten, L2 met de frequenties.
Werk met de pijltjestoetsen!
Gebruik nu twee lijsten voor de tabel hierboven, bijvoorbeeld:
L1 vul je met schoenmaten, L2 met de frequenties.
Werk met de pijltjestoetsen! Inhoud
| schoenmaat | frequentie |
| 39 | 2 |
| 40 | 1 |
| 41 | 5 |
| 42 | 5 |
| 43 | 9 |
| 44 | 4 |
| 45 | 3 |
| 46 | 1 |
Deze tabel kun je in je grafische rekenmachine invoeren in het STAT-menu:
 Gebruik nu twee lijsten voor de tabel hierboven, bijvoorbeeld:
L1 vul je met schoenmaten, L2 met de frequenties.
Werk met de pijltjestoetsen!
Gebruik nu twee lijsten voor de tabel hierboven, bijvoorbeeld:
L1 vul je met schoenmaten, L2 met de frequenties.
Werk met de pijltjestoetsen! 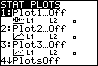 Nu je een frequentietabel hebt ingevoerd, kun je allerlei diagrammen maken met behulp van STAT PLOT. Je bereikt dat met: [2nd] [ Y= ].
Je krijgt dan het eerste venster hiernaast.
Nu je een frequentietabel hebt ingevoerd, kun je allerlei diagrammen maken met behulp van STAT PLOT. Je bereikt dat met: [2nd] [ Y= ].
Je krijgt dan het eerste venster hiernaast.
Kies je voor 1: Plot1, dan kun je het eerste diagram instellen, je ziet dan het tweede venster hiernaast.
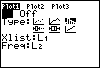 Kies voor On [ENTER] en loop met de pijltjestoetsen naar en door Type. Kies het type plaatje, controleer of Xlist op L1 en Freq op L2 staat ingesteld. Indien dat niet het geval is, zorg daar dan voor.
Door [GRAPH] te toetsen zou het gekozen diagram in beeld moeten komen, afhankelijk van de scherminstellingen.
Kies voor On [ENTER] en loop met de pijltjestoetsen naar en door Type. Kies het type plaatje, controleer of Xlist op L1 en Freq op L2 staat ingesteld. Indien dat niet het geval is, zorg daar dan voor.
Door [GRAPH] te toetsen zou het gekozen diagram in beeld moeten komen, afhankelijk van de scherminstellingen.
Om het histogram correct in beeld te krijgen moet je in [WINDOW] letten op de juiste instelling van Xmin (de linkergrens van de eerste staaf) en Xscl (de breedte van elke staaf).
Denk er om dat ook bij gehele getallen (zoals hier bij de schoenmaten) de staven een bepaalde breedte krijgen; je moet in feite altijd uitgaan van een klassenindeling en de waarnemingsgetallen opvatten als de klassemiddens. Bij de gegevens hierboven is het getal 39 dus eigenlijk de klasse 38,5 –< 39,5. De linkergrens van de eerste staaf is daarom 38,5 en de breedte van elke staaf is 1. Dus je moet het venster zo instellen dat Xmin = 38,5, Xmax = 46,5 (of iets meer), Xscl = 1, Ymin = 0 (of iets minder), Ymax = 9 (of iets meer) en Yscl = 1.
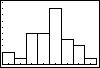
Met [TRACE] loop je over de middens van de bovenkanten van een staafdiagram, of kun je minimum, maximum, mediaan, kwartielen aflezen in een boxplot.
Breng achtereenvolgens met de gegevens hierboven in beeld: een staafdiagram, een lijndiagram, een boxplot. Zoek uit welk verschil er is tussen beide soorten boxplot in je TI83. Werk ook eens met andere gegevens, kies met name ook eens gegevens die in klassen zijn ingedeeld.
 Dus je vindt:
Dus je vindt: