Kansverdelingen met de TI-83
Met de TI-83 kun je in verschillende standaardsituaties kansen berekenen. In dit practicum komen de binomiale kansverdeling en de normale kansverdeling aan bod. Je moet voor dat je met dit practicum kunt werken bekend zijn met de basistechnieken van de TI-83 en het werken met functies op de TI-83. Doe eventueel eerst de bijbehorende practica.
Loop eerst het practicum: 'Simulaties en telsystemen met de TI-83' door.
Inhoud
De binomiale kansverdeling
Stel je voor dat je 100 keer hetzelfde kansexperiment uitvoert waarbij de kans op succes 0,23 en dus de kans op mislukking 1 – 0,23 = 0,77 is. De toevalsvariabele X stelt het aantal keren succes bij die 100 trekkingen voor. X heeft dan een binomiale kansverdeling met:
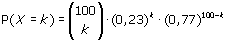
hierin is: 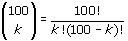 wat er op je TI-83 uitziet als 100 nCr k.
wat er op je TI-83 uitziet als 100 nCr k.
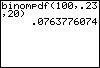
De kans op X = 20 is dan gewoon in je rekenvenster te bepalen door te tikken:

- [ ( ] 100 [MATH] ga naar PRB en kies 3: nCr en [ENTER]
- vervolg met [ ) ] [ × ] .23 [ ^ ] 20 [ × ] .77 [ ^ ] 80 en [ENTER]
Het antwoord zie je in het TI-venster hiernaast.
 Dit kan echter gemakkelijker. De TI-83 kent namelijk de functie 'binompdf' (binomial probability distribution function) waarmee kansen zoals die hierboven rechtstreeks zijn te berekenen:
Dit kan echter gemakkelijker. De TI-83 kent namelijk de functie 'binompdf' (binomial probability distribution function) waarmee kansen zoals die hierboven rechtstreeks zijn te berekenen:
- toets [2nd] [VARS], je hebt dan het DISTR-menu (distribution = verdeling)
- kies 0: binompdf( en [ENTER] (als je niet de pijltjestoetsen gebruikt maar alleen 0 toetst is [ENTER] overbodig)
- tik nu: 100 [ , ] .23 [ , ] 20 [ ) ] en [ENTER]
Je vindt dezelfde kans als hierboven.
De complete kansverdeling is nu eenvoudig te maken door de binomiale kans met een variabele X in het Y= scherm als functie in te voeren en dan een tabel met stapgrootte 1 bij die functie te maken. In de twee figuren hieronder zie je hoe dat er uit ziet:
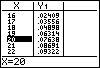
De hierboven gevonden waarde voor x = 10 vind je in de tabel terug.
Als een variabele X binomiaal is verdeeld met n = 100 en p = 0,23 dan kun je de volgende binomiale kansen berekenen met de TI-83:
- P(X = 20 | n = 100 en p = 0,23) = 0,0763...
- eerst: [2nd] [VARS] om naar het menu DISTR (distributions = verdelingen) te komen
- kies 0: binompdf( (en eventueel [ENTER])
- toets 100 [ , ] 0.23 [ , ] 20 [ ) ] [ENTER]
- P(X < 20 | n = 100 en p = 0,23) = 0,2810...
- [2nd] [VARS] en kies (met de pijltjestoetsen)
A: binomcdf( en [ENTER]
- toets 100 [ , ] 0.23 [ , ] 20 [ ) ] en [ENTER]
- P(X < 20 | n = 100 en p = 0,23) = P(X < 19 | n = 100 en p = 0,23) = 0,2046...
- [2nd] [VARS] en kies (met de pijltjestoetsen)
A: binomcdf( en [ENTER]
- toets 100 [ , ] 0.23 [ , ] 19 [ ) ] en [ENTER]
- P(X > 20 | n = 100 en p = 0,23) =
1 – P(X < 20 | n = 100 en p = 0,23) = 0,7189...
- toets 1 [ – ] [2nd] [VARS] en kies A: binomcdf( en [ENTER]
- toets daarna 100 [ , ] 0.23 [ , ] 20 [ ) ] en [ENTER]
- P(X > 20 | n = 100 en p = 0,23) = 1 – P(X < 19 | n = 100 en p = 0,23) = 0,7953...
- toets 1 [ – ] [2nd] [VARS] en kies A: binomcdf( en [ENTER]
- en daarna 100 [ , ] 0.23 [ , ] 19 [ ) ] en [ENTER]

Grenswaarden bij binomiale toetsing
Vooral bij het toetsen van hypothesen wil je grenswaarden opzoeken bij binomiale kansverdelingen. Het gaat dan om problemen als:
Bepaal de waarde van g waarvoor:
P(X < g | n = 100 en p = 0,23) < 0,10.
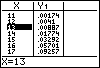
Je moet daarvoor zelf een cumulatieve kansverdeling maken voor de binomiale toevalsvariabele X met n = 100 en p = 0,23. Dat doe je door deze kansverdeling in te voeren als functie in het Y= scherm en dan de tabel van die functie (stapgrootte 1) in beeld te brengen. In de twee figuren hieronder zie je hoe dat er uit ziet.
De gezochte grenswaarde is kennelijk g = 13.


Kanshistogrammen, verwachting en standaarddeviatie
Bij een binomiale kansverdeling kun je een kanshistogram maken.
Je laat dan de grafische rekenmachine een lijst met kansen maken. Stel bijvoorbeeld dat je een kanshistogram wilt maken bij een binomiale verdeling met n = 100 en p = 0,23.
Dat kun je zo doen:
- Toets [STAT] en kies 1: Edit...
Je ziet nu een aantal lijsten L1, L2, enzovoorts.
- Voer in L1 de waarden voor de stochast X = 0, 1, 2, ..., 100 in door de cursor op L1 te zetten en [ENTER] te toetsen. Onderaan zie je nu L1= met daarachter de cursor.
- Ga naar [2nd] [STAT] [OPS] en kies 5: seq en [ENTER].
Je ziet nu: L1=seq( met daarachter de cursor.
- Zet daar in: X [ , ] X [ , ] 0 [ , ] 100 [ ) ] en toets [ENTER].
In L1 staan nu de getallen 0 t/m 100. Ga dat na door met de pijltjes toetsen door de lijst te lopen.
- Voer in L2 de kansen in door de cursor op L2 te zetten en [ENTER] te toetsen. Onderaan zie je nu L2= met daarachter de cursor.
Ga naar [2nd] [STAT] [OPS] en kies 5: seq en [ENTER].
Je ziet nu: L2=seq( met daarachter de cursor.
- Ga naar: [2nd] [VARS] en kies 0: binompdf en toets [ENTER]
Je ziet nu: L2=seq(binompdf( met daarachter de cursor.
-
 Vul in: 100, 0.23, X [ ) ] [ , ] X [ , ] 0 [ , ] 100 [ ) ] en toets [ENTER]. Nu staan in L2 de bijbehorende kansen. Controleer dat.
Vul in: 100, 0.23, X [ ) ] [ , ] X [ , ] 0 [ , ] 100 [ ) ] en toets [ENTER]. Nu staan in L2 de bijbehorende kansen. Controleer dat.
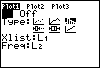
- Nu je de lijsten L1 en L2 hebt ingevoerd, kun je diagrammen maken met behulp van STAT PLOT. Je bereikt dat met: [2nd] [ Y= ]. Je krijgt dan de figuur hiernaast.
-
Kies je voor 1: Plot1 en [ENTER], dan kun je het eerste diagram instellen, je ziet dan de tweede figuur hiernaast.
- Kies voor On [ENTER] en loop met de pijltjestoetsen naar en door Type.
Kies het type plaatje, controleer of Xlist op L1 en Freq op L2 staat ingesteld. Indien dat niet het geval is, zorg daar dan voor (Je vindt L1, L2, enzovoorts op de cijfertoetsen via [2nd]). Door [GRAPH] te toetsen zou het gekozen diagram in beeld moeten komen, afhankelijk van de scherminstellingen. Omdat er alleen voor X van 10 t/m 40 kansen uitkomen die in beeld zijn te brengen, stel je voor X ook die waarden in. De uitkomsten liggen dan tussen 0 en 0,15.
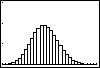
Oefen jezelf door zo een paar kanshistogrammen bij de binomiale verdeling te maken. Cumulatieve kanshistogrammen lukken ook.
Centrum en spreiding van een kanshistogram
Als je een kansverdeling als lijst in de TI-83 hebt ingevoerd (zie de voorgaande tekst), dan kun je eenvoudig een maat voor het centrum van de verdeling en een maat voor de spreiding van de verdeling vinden.
- De gebruikte centrummaat voor de kansverdeling van X is de verwachting, aangegeven met μX of
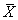 .
.
- De gebruikte spreidingsmaat heet de standaardafwijking of standaarddeviatie, aangegeven met σX.
Om deze centrum- en spreidingsmaten in één keer in beeld te krijgen, ga je zo te werk:
- Toets [STAT], kies CALC en dan 1: 1-Var Stats
- Toets daar achter de namen (bijvoorbeeld L1 en L2) van de twee lijsten die je in gebruik hebt voor je gegevens. Eerst de lijst (L1) waarnemingsgetallen, dan na [ , ] de lijst (L2) met kansen (relatieve frequenties)
- In je scherm staat nu: 1-Var Stats L1, L2
Toets [ENTER] en je krijgt de juiste waarden.
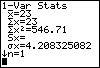 Doe dit met de binomiale kansverdeling uit de voorgaande tekst. In het plaatje zie je het eindresultaat. De verwachting is dus 23 en de standaarddeviatie in ongeveer 4,21.
Doe dit met de binomiale kansverdeling uit de voorgaande tekst. In het plaatje zie je het eindresultaat. De verwachting is dus 23 en de standaarddeviatie in ongeveer 4,21.

De normale kansverdeling
Als een toevalsvariabele X normaal is verdeeld met een gemiddelde van μX = 100 en een standaardafwijking van σX = 6, dan kun je de volgende kansen berekenen met de TI83:
- P(95 < X < 102 | μX = 100 en σX = 6) ≈ 0,4282...
- toets [2nd] [VARS] om naar het menu DISTR (distributions = verdelingen) te komen
- kies dan 2: normalcdf( en toets: 95 [ , ] 102 [ , ] 100 [ , ] 6 [ ) ] en [ENTER]
- P(X < 95 | μX = 100 en σX = 6) ≈ 0,2023...
- toets [2nd] [VARS] en kies 2: normalcdf(
- toets [ (-) ] 1000 [ , ] 95 [ , ] 100 [ , ] 6 [ ) ] en[ENTER]
- P(X > 95 | μX = 100 en σX = 6) ≈ 0,7976...
- toets [2nd] [VARS] kies 2: normalcdf(
- toets 95 [ , ] 1000 [ , ] 100 [ , ] 6 [ ) ] en [ENTER]
Loop al deze berekeningen zelf na!
Bij een normale kansverdeling kun je op de TI-83 de te berekenen kansen als oppervlakte onder de normaalkromme in beeld brengen. Daartoe gebruik je het menu DISTR.
Stel je voor dat je de volgende kans wilt berekenen en in beeld brengen als oppervlakte onder de normale verdeling:
P(95 < X < 102 | μX = 100 en σX = 6) ≈ 0,4282...
Je voorziet eerst je grafiekenscherm van de goede instellingen, bijvoorbeeld X laat je tussen 80 en 120 lopen en Y (dat zijn de waarden bij de normaalkromme) tussen –0,1 en 0,2. Zorg dat er geen functies meer zijn ingevoerd, anders krijg je daarvan misschien ook nog de grafieken in beeld.
Vervolgens toets je:
- [2nd] [VARS] en naar DRAW en je kiest 1: ShadeNorm( [ENTER]
- in het rekenscherm zet je: ShadeNorm(95,102,100,6) en [ENTER]
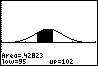 De figuur hiernaast komt dan in beeld.
De figuur hiernaast komt dan in beeld.
Met [2nd] [PRGM] 1: ClrDraw [ENTER] gaat een figuur weer weg.

Grenswaarden bij normale kansverdelingen
Terugrekenen vanuit gegeven kansen bij de normale verdeling kan ook gemakkelijk met de TI-83.
Je wilt dan bij een normaal verdeelde variabele X bij een gegeven kans de bijbehorende grenswaarde g voor X terugzoeken:
- P(X < g | μX = 100 en σX = 6) ≈ 0,2023 geeft: g ≈ 95
- toets [2nd] [VARS] en kies 3: invNorm(
- toets 0.2023 [ , ] 100 [ , ] 6 [ ) ] [ENTER]
- P(X > g | μX = 100 en σX = 6) ≈ 0,2023 geeft: g ≈ 105
Omdat P(X > g) = 1 – P(X < g), is nu: P(X < g) = 1 – 0,2023 = 0,7977. Daarom:
- toets [2nd] [VARS] en kies 3: invNorm(
- toets 0.7977 [ , ] 100 [ , ] 6 [ ) ] [ENTER]
Loop ook deze berekeningen zorgvuldig na!

Gemiddelde of standaarddeviatie bij normale kansverdeling berekenen
Als je met kansen te maken hebt bij een normale verdeling, dan werk je altijd met normalcdf.
Je kunt in het Y= scherm de cumulatieve normale verdeling normalcdf invoeren. En dat is handig bij het bepalen van kansen en vooral bij het terugrekenen vanuit een gegeven kans.
Stel je voor dat je de volgende kans wilt berekenen:
P(X < 102 | μX = 100 en σX = 6) ≈ 0,2023...
Je voorziet eerst je grafiekenscherm van de goede instellingen, bijvoorbeeld laat je X lopen tussen 80 en 120 en laat je Y (dat zijn de kansen bij de cumulatieve normaalkromme) tussen –0,1 en 1. Zorg dat er geen functies zijn ingevoerd, anders krijg je daarvan misschien ook nog de grafieken in beeld. Vervolgens toets je:
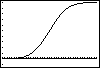
- [ Y= ] om het invoerscherm te openen;
- [2nd] [VARS] en je kiest 2: normalcdf( [ENTER];
- in het Y= scherm zet je: normalcdf(0,X,100,6) en [ENTER].
De figuur hiernaast komt dan in beeld.
Toets je nu [TRACE] dan kun je met de cursor over de grafiek lopen en kansen bepalen. Dat is echter nogal grof.
Via het Calc-menu en Value kun je echter de gevraagde kans bepalen: 0,6305...
Op deze manier kun je gemakkelijk terugrekenen vanuit een gegeven kans.
Stel je voor dat je g wilt berekenen als:
P(X < g | μX = 100 en σX = 6) ≈ 0,6
Je voert dan voor Y1 de cumulatieve normaalkromme in (net als hiervoor) en voor Y2 de gegeven kans 0,6.
Met behulp van intersect vind je dat g = 101,52...
Verder kun je de standaardafwijking bepalen als bijvoorbeeld:
P(X <102 | μX = 100 en σX = ??) ≈ 0,6
Je gaat dan zo te werk:
- Voer in Y1 = normalcdf(0,102,100,X) en Y2 = 0.6
- Stel het venster zo in dat X (dat is nu de standaarddeviatie!) loopt van 0 tot zeg 20 en Y loopt van 0 tot 1 (cumulatieve kansen)
- Met intersect vind je nu als standaarddeviatie 7,8943...
Tenslotte kun je het gemiddelde bepalen als bijvoorbeeld:
P(X <102 | μX = ?? en σX = 6) ≈ 0,6
Je gaat dan zo te werk:
- Voer in Y1 = normalcdf(0,102,X,6) en Y2 = 0.6
- Stel het venster zo in dat X (dat is nu het gemiddelde!) loopt van 80 tot 120 en Y loopt van 0 tot 1 (cumulatieve kansen)
- Met intersect vind je nu als gemiddelde 100,4799...

 Math4all
Math4all
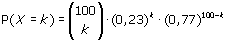
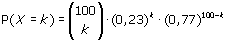
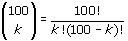 wat er op je TI-83 uitziet als 100 nCr k.
wat er op je TI-83 uitziet als 100 nCr k. 
 Dit kan echter gemakkelijker. De TI-83 kent namelijk de functie 'binompdf' (binomial probability distribution function) waarmee kansen zoals die hierboven rechtstreeks zijn te berekenen:
Dit kan echter gemakkelijker. De TI-83 kent namelijk de functie 'binompdf' (binomial probability distribution function) waarmee kansen zoals die hierboven rechtstreeks zijn te berekenen:




 Vul in: 100, 0.23, X [ ) ] [ , ] X [ , ] 0 [ , ] 100 [ ) ] en toets [ENTER]. Nu staan in L2 de bijbehorende kansen. Controleer dat.
Vul in: 100, 0.23, X [ ) ] [ , ] X [ , ] 0 [ , ] 100 [ ) ] en toets [ENTER]. Nu staan in L2 de bijbehorende kansen. Controleer dat.

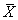 .
. 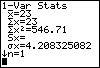 Doe dit met de binomiale kansverdeling uit de voorgaande tekst. In het plaatje zie je het eindresultaat. De verwachting is dus 23 en de standaarddeviatie in ongeveer 4,21.
Doe dit met de binomiale kansverdeling uit de voorgaande tekst. In het plaatje zie je het eindresultaat. De verwachting is dus 23 en de standaarddeviatie in ongeveer 4,21.
 De figuur hiernaast komt dan in beeld.
De figuur hiernaast komt dan in beeld.
