Functies en de TI-83/84
De TI-83/84 kan je behulpzaam zijn bij het werken met functies. Bijvoorbeeld kun je gemakkelijk nulpunten, snijpunten, oppervlakte onder een grafiek, de helling van een grafiek bepalen. Verder kun je functies eenvoudig combineren, zelfs schakelen.
Loop eerst het practicum: 'Basistechnieken TI-83/84' door.
Inhoud
Functiewaarden, nulpunten en toppen
Je weet hoe je een functie kunt invoeren via Y=.
Als je eenmaal een functie hebt ingevoerd, kun je er met de verschillende toetsen direct onder het beeldscherm van alles mee doen.
De toetsen [WINDOW], [ZOOM], [TRACE] en natuurlijk [GRAPH] heb je al regelmatig gebruikt. Er zijn echter meer mogelijkheden.
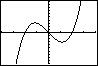 Bekijk de grafiek van de functie:
Bekijk de grafiek van de functie:
y1(x) = x3 – 4x
Breng hem netjes in beeld, kies zodanige vensterinstellingen dat x loopt vanaf –4 t/m 4 en y loopt vanaf –10 t/m 10.
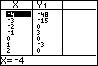 Met [2nd] [GRAPH] bereik je TABLE, waar je een tabel van de functie kunt zien. Met behulp van [2nd] [WINDOW] bereik je TBLSET, waar je de instellingen van de tabel kunt aanpassen.
Doe dat tot je de tabel hiernaast krijgt.
Met [2nd] [GRAPH] bereik je TABLE, waar je een tabel van de functie kunt zien. Met behulp van [2nd] [WINDOW] bereik je TBLSET, waar je de instellingen van de tabel kunt aanpassen.
Doe dat tot je de tabel hiernaast krijgt.
Hieruit zijn de karakteristieken van de grafiek van deze functie (de nulpunten en de toppen) eenvoudig af te lezen.
 Deze karakteristieken zijn ook te bepalen als de functie minder eenvoudig in beeld is te krijgen.
Daartoe heeft de TI83 het CALC-menu (calculate = rekenen). Je roept dat op met: [2nd] [TRACE].
Deze karakteristieken zijn ook te bepalen als de functie minder eenvoudig in beeld is te krijgen.
Daartoe heeft de TI83 het CALC-menu (calculate = rekenen). Je roept dat op met: [2nd] [TRACE].
Met de zeven routines in het CALC-menu kun je van alles over de grafiek te weten komen:
- Met 1: value (value = waarde) bereken je een functiewaarde bij een x-waarde die je zelf mag opgeven. Probeer maar ...
- Met 2: zero (zero = nul) bereken je nulpunten. Dat gaat zo:
- Kies 2: zero [ENTER]
- De rekenmachine vraagt nu een linkergrens (Left Bound ?) voor x. Loop dan met de cursor over de grafiek tot je links van het nulpunt bent uitgekomen en [ENTER].
- De rekenmachine vraagt nu een rechtergrens (Right Bound ?) voor x. Loop dan met de cursor over de grafiek tot je rechts van het nulpunt bent uitgekomen en [ENTER].
- De rekenmachine vraagt nu of zijn gokje (Guess ?) goed is en je doet: [ENTER].
- Als het goed is komt nu (een benadering van) het nulpunt (zowel x als y in beeld onderaan het scherm.
Controleer dat (–2,0), (0,0) en (2,0) de nulpunten van y1 zijn.
- Met 3: minimum en 4: maximum kun je toppen berekenen. Dat gaat vrijwel net zo als bij nulpunten.
Controleer dat (1,155; –3,079) en (–1,155; 3,079) de toppen van de grafiek van y1 zijn.

Snijpunten van twee functies
Voor het bepalen van de snijpunten van de grafieken van twee functies kun je TABLE of TRACE gebruiken.
Dit gaat echter sneller met het CALC-menu.
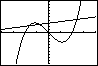 Gebruik de functies
Gebruik de functies
y1 = x3 – 4x en
y2 = 0,5x + 3
Als je beide invoert met dezelfde instellingen als je hiervoor alleen voor de grafiek van y1 hebt gebruikt, krijg je de drie snijpunten keurig in beeld. Met TRACE of met TABLE kun je ze wellicht vinden.
Met CALC gaat dat zo:
- Kies in het CALC-menu 5: intersect [ENTER].
- Je moet nu in de buurt van het gewenste snijpunt gaan staan met de cursor.
- De rekenmachine vraagt of dit één van de twee grafieken is (First curve ?). Als dat niet zo is (er kunnen nog wel veel meer grafieken in je scherm staan dan die van y1 en y2, dan ga je met de pijltjestoetsen (omhoog en/of omlaag) naar een gewenste grafiek en [ENTER]. Als dat wel zo is, toets je meteen [ENTER].
- De rekenmachine vraagt of dit de andere grafiek is (Second curve ?). Als dat zo is, doe je weer [ENTER].
- Vervolgens vraagt de rekenmachine of zijn gok (Guess?) juist is. Nu kun je in de buurt van het gewenste snijpunt gaan staan en [ENTER].
- Nu wordt het dichtstbijzijnde snijpunt van y1 en y2 berekend.
Bereken de snijpunten van de grafieken van f en g. Als het goed is vind je (in drie decimalen nauwkeurig):
(–1,631; 2,184), (–0,767; 2,617) en (2,398; 4,199).

Functies combineren
Je kunt met de TI-83 eenmaal ingevoerde functies ook bij andere functies weer oproepen als Y1, Y2, enzovoorts.
Ga weer uit van de reeds ingevoerde functies f en g voor respectievelijk Y1 en Y2.
- Als je de grafiek van y3 = y1 + 2y2 wilt onderzoeken, dan voer je die functie y3 bij Y3 als volgt in: Y3=Y1+2*Y2.
Je vindt daarbij Y1 en Y2 in het menu VARS.
- Toets: [VARS] en kies Y-VARS 1: Function [ENTER].
- Daar kun je dan de gewenste y-variabele Y1, Y2, ..., Y9, Y0 kiezen.
Bekijk de grafiek van y3 maar eens.
- Als je de grafiek van y4 = y1(x + 1) wilt bekijken, dan voer je bijvoorbeeld bij Y4 in: Y4=Y1(X+1).
De grafiek van y4 is nu eenvoudig te bekijken.
Als je daarbij de grafiek van y2 maar lastig vindt, dan zet je die even uit door in het Y= scherm met de cursor op het = teken achter Y2 te gaan staan en [ENTER] te toetsen: Y2 is nu 'uit', er komt geen grafiek van in het scherm.
Vergelijk de grafieken van y1 en y4. Probeer te bedenken wat het verband tussen beide is.
-
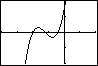 Tenslotte kun je functies schakelen.
Bijvoorbeeld vind je de grafiek van y5 = y1(y2(x)) door bij Y5 in te voeren: Y5=Y1(Y2(X)).
Tenslotte kun je functies schakelen.
Bijvoorbeeld vind je de grafiek van y5 = y1(y2(x)) door bij Y5 in te voeren: Y5=Y1(Y2(X)).
Bekijk de grafiek van y5 maar eens. Je ziet hem hiernaast, kun je hem zo in beeld brengen?
Even oefenen?
Bepaal de karakteristieken van de volgende functies:
- y1(x) = 0,5x4 – 2x2
- y2(x) = y1(x – 2)
- y3(x) = 4 – x2
- y4(x) = y1(x) + y3(x)
- y5(x) = y1(0,5x) + 4

Families van functies
Je kunt ook hele series functies invoeren die ongeveer hetzelfde functievoorschrift hebben.
Alle rechte lijnen door (0, 3) bijvoorbeeld hebben het functievoorschrift:
y(x) = ax + 3.
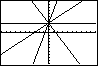
Stel je voor dat je van deze rechte lijnen de grafieken wilt zien voor a = –2, a = 0, a = 1 en a = 4.
Je maakt dan eerst een lijst van deze vier getallen: {–2,0,1,4} naar L1.
Je toetst dit zo in:
[2nd] [ ( ] [(–)] 2 [ , ] 0 [ , ] 1 [ , ] 4 [2nd] [ ) ] [STO>] [2nd] [ 1 ].
 Ga dat na.
Ga dat na.
Vervolgens voer je de functie bij Y2 zo in: Y2=L1*X+3.
Met [GRAPH] krijg je de grafiek van Y1 en de vier rechte lijnen bij Y2 te zien (als je alle andere functies weghaalt of uit zet).
Op dezelfde manier kun je grafieken bij andere families van functies tekenen.

Hellingen van functies
Je kunt met de TI-83 op een aantal manieren de helling van een grafiek in een bepaald punt berekenen. Je spreekt wel van het hellingsgetal of de hellingwaarde van een functie f voor een bepaalde waarde van x.
Je kunt zo'n hellingsgetal vinden met behulp van het CALC-menu.
Gebruik nog steeds de functie y1 die aan het begin van dit practicum is gegeven. Verwijder alle andere functies uit je TI-83.
Stel je voor dat je het hellingsgetal voor x = 3 wilt berekenen. Dat kan zo:
- Kies in het CALC-menu voor 6: dy/dx en [ENTER].
- Tik vervolgens de gewenste x-waarde 3 en [ENTER].
- Je vindt nu het gewenste hellingsgetal 23. (Er staat een benadering, meestal niet het preciese hellingsgetal.)
Je kunt ook aan de grafiek van y1 een lijn tekenen die voor x = 3 de gewenste helling heeft, een raaklijn aan de grafiek van y1 voor x = 3. Dat gaat via het DRAW-menu (to draw = tekenen).
- Toets: [2nd][PRGM] en kies 5: Tangent( [ENTER]
- In het gewone rekenscherm zie je nu: Tangent( met daar achter de cursor. Maak deze regel af tot: Tangent(Y1,3) en [ENTER] en je ziet de raaklijn ontstaan.
Je haalt een lijn die getekend is via het DRAW-menu weg door [2nd][PRGM] te toetsen en bij DRAW 1: ClrDraw te kiezen en [ENTER].
Bereken nu zelf het hellingsgetal van y1 voor x = –1 en teken de bijbehorende raaklijn.
Ook een complete hellingsgrafiek is mogelijk.
Als je intoetst:
Y2=(Y1(X+0.001)–Y1(X))/0.001
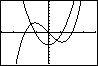 dan is de grafiek van Y2 een goede benadering voor de hellingsgrafiek van de gegeven functie y1.
dan is de grafiek van Y2 een goede benadering voor de hellingsgrafiek van de gegeven functie y1.
Breng zelf deze hellingsgrafiek van y1 in beeld.

Oppervlakte onder de grafiek
Tenslotte kun je met het CALC-menu de oppervlakte tussen de grafiek en de horizontale as bepalen.
Neem nog eens de grafiek van y1.
- Kies bij het CALC-menu 7: Sf(x)dx en [ENTER]
- Je krijgt dan de grafiek en een vraag naar de linkergrens (Lower Limit ?) van het gebied onder de grafiek waarvan je de oppervlakte wilt bepalen. Loop met je cursor naar het gewenste punt, of toets de gewenste x-waarde. Toets vervolgens [ENTER].
- Vervolgens wordt de rechtergrens (Upper Limit ?) gevraagd. Voer de gewenste waarde in en [ENTER].
- Het bedoelde gebied wordt nu 'ingekleurd' en de oppervlakte komt onderaan het scherm in beeld.
Met ClrDraw in het DRAW-menu haal je de inkleuring weer weg.
Bepaal zelf de oppervlakte tussen de grafiek van y1 en de x-as tussen x = 0 en x = 4.
Je vindt als alles goed gaat 32.

Functies die uit meerdere delen bestaan
Soms bestaat een functie uit meerdere delen.
Stel je voor dat het voorschrift van een functie f luidt:
f(x) = –2x als x kleiner is dan 1
f(x) = 2x als x groter of gelijk is aan 1
Om zo'n functie te kunnen invoeren in je grafische rekenmachine maak je gebruik van het TEST-menu (via [2nd][MATH]).
Daarmee kun je de kleiner- en de grotertekens invoeren (ook kleiner-of-gelijk en groter-of-gelijk).
Hier zie je hoe je zo'n functie invoert met daarnaast het resultaat.
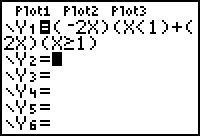
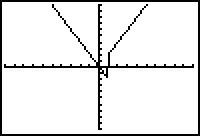
Het verticale lijntje in de grafiek hoort er eigenlijk niet te zijn. Het ontstaat omdat de TI-83 alle berekende punten domweg met elkaar verbindt, ook als die verbindingslijn geen punten van de grafiek bevat.

 Math4all
Math4all
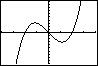 Bekijk de grafiek van de functie:
Bekijk de grafiek van de functie:
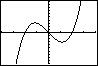 Bekijk de grafiek van de functie:
Bekijk de grafiek van de functie:
 Met [2nd] [GRAPH] bereik je TABLE, waar je een tabel van de functie kunt zien. Met behulp van [2nd] [WINDOW] bereik je TBLSET, waar je de instellingen van de tabel kunt aanpassen.
Doe dat tot je de tabel hiernaast krijgt.
Met [2nd] [GRAPH] bereik je TABLE, waar je een tabel van de functie kunt zien. Met behulp van [2nd] [WINDOW] bereik je TBLSET, waar je de instellingen van de tabel kunt aanpassen.
Doe dat tot je de tabel hiernaast krijgt.
 Deze karakteristieken zijn ook te bepalen als de functie minder eenvoudig in beeld is te krijgen.
Daartoe heeft de TI83 het CALC-menu (calculate = rekenen). Je roept dat op met: [2nd] [TRACE].
Deze karakteristieken zijn ook te bepalen als de functie minder eenvoudig in beeld is te krijgen.
Daartoe heeft de TI83 het CALC-menu (calculate = rekenen). Je roept dat op met: [2nd] [TRACE].
 Gebruik de functies
Gebruik de functies
 Tenslotte kun je functies schakelen.
Bijvoorbeeld vind je de grafiek van y5 = y1(y2(x)) door bij Y5 in te voeren: Y5=Y1(Y2(X)).
Tenslotte kun je functies schakelen.
Bijvoorbeeld vind je de grafiek van y5 = y1(y2(x)) door bij Y5 in te voeren: Y5=Y1(Y2(X)).  Ga dat na.
Ga dat na.  dan is de grafiek van Y2 een goede benadering voor de hellingsgrafiek van de gegeven functie y1.
dan is de grafiek van Y2 een goede benadering voor de hellingsgrafiek van de gegeven functie y1. 
