Rekentaak 6: Verhoudingen en schaal
Werk zonder rekenmachine! Het gaat hier om het handmatig en uit het hoofd rekenen...
Schaallijnen
Bestudeer eerst:
 www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Meten en tekenen > Schaallijnen
www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Meten en tekenen > Schaallijnen
Opgaven
-
Hier zie je een deel van de kaart van Deventer.
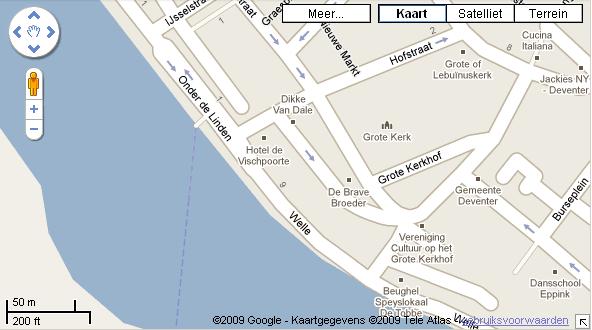
De schaal van de kaart is aangegeven door een schaallijntje. Je kunt daarom nameten hoe lang 50 m op de kaart is.
-
Hoe lang is 50 m op de kaart? (Je antwoord hangt af van het beeldscherm of de uitdraai die uit je printer komt.)
-
Als 50 m overeen komt met 2 cm, hoeveel m is dan elke cm op de kaart? En wat is dan de schaal?
-
Hoeveel bedraagt jouw schaal voor deze kaart?
Op het kaartje zijn bepaalde gebouwen met een klein blokje aangegeven.
De afstand tussen twee van die gebouwen meet je dan van blokje tot blokje.
-
Je gaat vanuit Hotel de Vischpoorte door de Hofstraat naar de kookwinkel Cuccina Italia.
Hoeveel m is dat in werkelijkheid ongeveer?
-
Hier zie je twee schaallijntjes van 6 cm lengte. Schrijf bij elke schaallijn de juiste schaal.
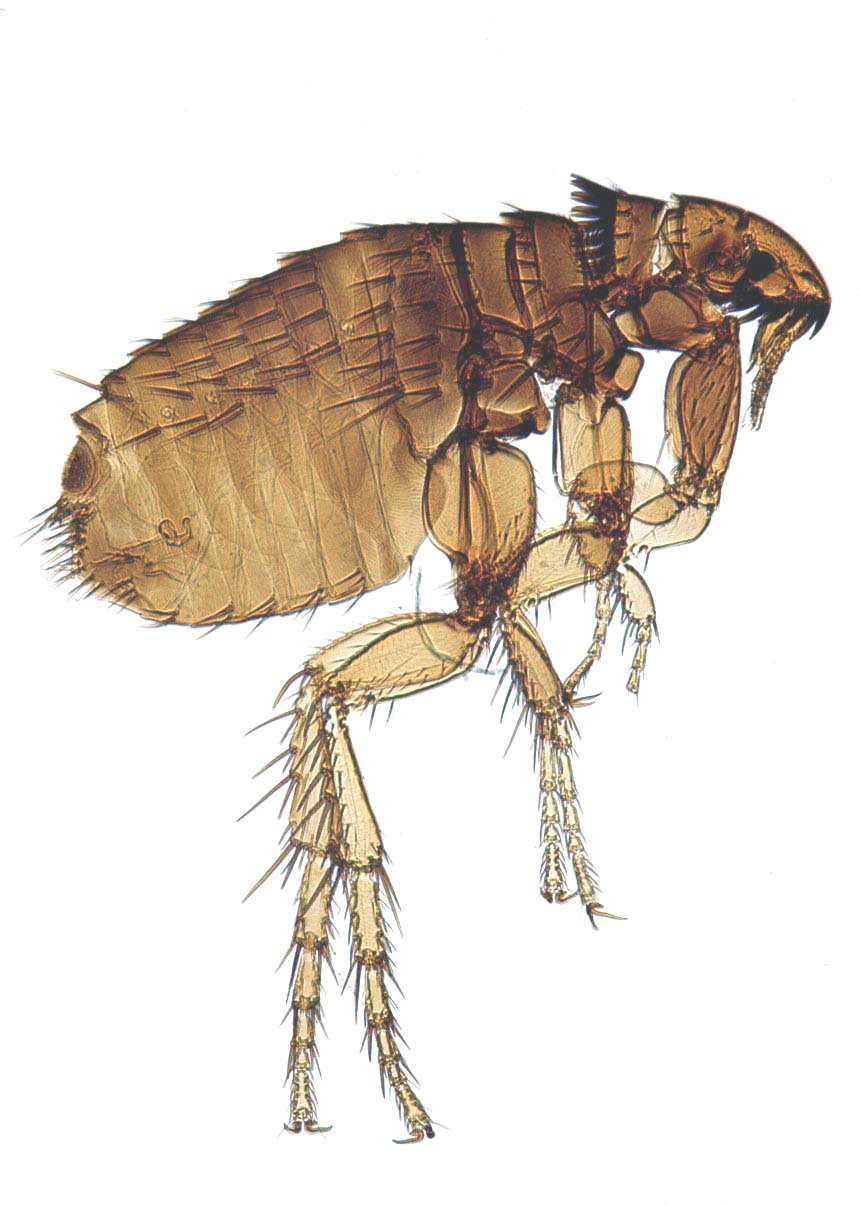
-
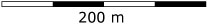 schaal 1 : ...
schaal 1 : ...
-
 schaal 1 : ...
schaal 1 : ...
-
Een vlo is getekend op schaal 10 : 1. Hij is 3 cm lang.
-
Hoe lang is die vlo in werkelijkheid?
-
Op welke schaal is deze foto van een vlo gemaakt?
-
Een vlo kan 40 keer zijn eigen lengte springen. Hoeveel mm is dat?
-
Een olifant is in werkelijkheid 3 m hoog. Hij is getekend op schaal 1 : 100.
Naast de olifant staat een muis getekend, in de tekening zijn beide even hoog.
-
Hoe hoog is de olifant in de tekening?
-
De muis is in werkelijkheid 9 cm hoog. Op welke schaal is de muis getekend?
-
Hoeveel keer zo hoog is de olifant ten opzichte van de muis in werkelijkheid?
-
Hier zie je een wandeling ("Drie Kieften" route) in de buurt van Joppe.
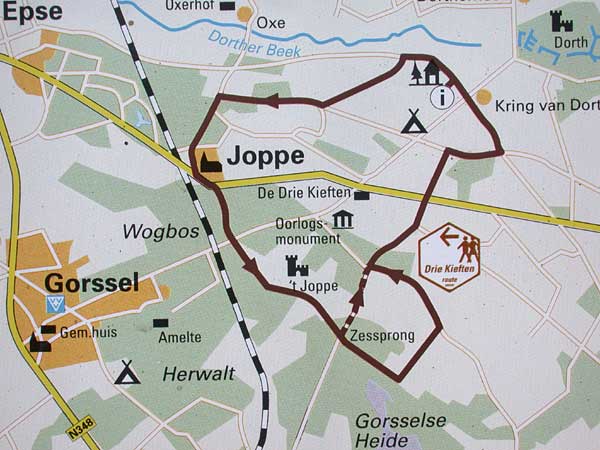
Neem aan dat de kaart is getekend op schaal 1 : 50000.
-
Hoe groot is dan de afstand van de VVV van Gorsel naar "De Drie Kieften" in werkelijkheid?
-
Schat hoe groot de wandeling in werkelijkheid is op 0,5 km nauwkeurig.
Ga er van uit dat je niet de verkorte route loopt.
-
Van het centrum van Deventer naar dat van Zutphen is 13 km.
Je hebt een kaart waarop die afstand 6,5 cm is.
Wat is de schaal van die kaart?
 Hier zie je een foto van de maan.
De diameter van de maan is ongeveer 3476 km.
Hier zie je een foto van de maan.
De diameter van de maan is ongeveer 3476 km.
Op welke schaal wordt de maan op deze foto weergegeven?
Oppervlaktevergroting
Bestudeer eerst:
 www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Meten en tekenen > Vergroten
www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Meten en tekenen > Vergroten
Opgaven
-
Een rechthoek is 6 cm lang en 4 cm breed.
Een andere rechthoek heeft 3 keer zo grote afmetingen.
-
Welke oppervlakte heeft de eerste rechthoek?
-
Welke oppervlakte heeft de tweede rechthoek?
-
Hoeveel keer zo groot wordt de oppervlakte van de tweede rechthoek in vergelijking met de eerste?
-
Een voetbalveld is getekend op schaal 1 : 1000.
In de tekening is het 12 cm lang en 7,5 cm breed.
-
Hoe groot is dit voetbalveld in werkelijkheid?
-
Met welk getal moet je de afmetingen van dit veld vermenigvuldigen om de werkelijke afmetingen te krijgen?
-
Hoe groot is de oppervlakte van het voetbalveld op de tekening?
-
Met welk getal moet je de oppervlakte van dit veld vermenigvuldigen om de werkelijke oppervlakte te krijgen?
-
Hoeveel m2 is die werkelijke oppervlakte?
-
Op een kaart met een schaal van 1 : 200 heeft een bouwkavel een oppervlakte van 16 cm2.
Hoeveel m2 is de oppervlakte van deze kavel in werkelijkheid?
-
Een raam heeft een oppervlakte van 1,2 m2.
Een tweede raam heeft afmetingen die precies 2,5 keer zo groot zijn dan het eerste.
-
Hoeveel m2 is de oppervlakte van dit tweede raam?
-
Een derde raam heeft een oppervlakte van 4,8 m2.
Hoeveel keer zo groot zijn de afmetingen van dit derde raam ten opzichte van het eerste?
-
Hoeveel keer zo groot zijn de afmetingen van dit derde raam ten opzichte van het tweede raam?
-
Een rechthoekig weiland van 2,5 hectare (dat is 2,5 hm2) heeft op een kaart een oppervlakte van 100 cm2.
Wat is de schaal van die kaart?
-
De gemeente Deventer heeft een oppervlakte van 134,37 km2.
Op een kaart is die oppervlakte nog 1,3437 cm2.
Wat is de schaal van die kaart?
Inhoudsvergroting
 www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Meten en tekenen > Vergroten
www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Meten en tekenen > Vergroten
Opgaven
-
Een kubus heeft ribben van 5 cm.
Een tweede kubus heeft 4 keer zo grote afmetingen.
-
Hoe groot zijn de ribben van de tweede kubus?
-
De oppervlakte van de eerste kubus is `6 xx 25 = 150` cm2. Waarom?
-
Hoeveel bedraagt de oppervlakte van de tweede kubus?
-
Hoeveel bedraagt de inhoud van de eerste kubus?
-
Hoeveel bedraagt de inhoud van de tweede kubus?
-
Geef de lengtevergrotingsfactor, de oppervlaktevergrotingsfactor en de inhoudsvergrotingsfactor.
-
Een kunstenaar maakt eerst een schaalmodel, alvorens het definitieve beeld wordt gemaakt.
De afmetingen van het echte beeld moeten 20 keer zo groot worden als die van het schaalmodel.
Het schaalmodel heeft een oppervlakte van 1400 cm2 en een volume van 3000 cm3.
Bereken de oppervlakte en de inhoud van het echte beeld.
-
De Aarde heeft een omtrek van ongeveer 40000 km, een oppervlakte van ongeveer 511000000 km2 en een inhoud van ongeveer `1,087 * 10^12` km3.
Je maakt een schaalmodel op schaal 1 : 1000000.
Bereken de omtrek, de oppervlakte en de inhoud van het schaalmodel.
-
Je kunt een bepaalde drank kopen in kleine flesjes van 0,25 L en in grote flessen van 1,5 L.
Beide soorten flessen hebben precies dezelfde vorm.
-
Hoeveel keer zo groot is de hoogte van de grote fles als de hoogte van de kleine fles?
-
Hoeveel keer zoveel glasoppervlakte heeft de grote fles als de kleine fles?
-
Je hebt twee maatbekers: de rechter heeft een 3,375 keer zo grote inhoud dan de linker.
De linker maatbeker wordt gemaakt van 400 cm2 metaalplaat.
Hoeveel metaal is er nodig voor de rechter maatbeker?
Door elkaar...
Opgaven
 Bij een schaalmodel van een voorwerp worden alle lengtes met een vaste vergrotingsfactor verkleind. Dit model van een Smart ForTwo heeft een schaal van 1 : 18.
Bij een schaalmodel van een voorwerp worden alle lengtes met een vaste vergrotingsfactor verkleind. Dit model van een Smart ForTwo heeft een schaal van 1 : 18.
De afmetingen van een echte Smart ForTwo van deze versie zijn: lengte 250 cm, breedte 152 cm en hoogte 155 cm. De cilinderinhoud van de motor is 698 cc (1 cc = 1 cm3) en er past 33 L benzine in de tank. De totale glasoppervlakte is ongeveer 3,2 m2.
-
Bereken de lengte, de breedte en de hoogte van het schaalmodel in cm nauwkeurig.
-
Bereken de glasoppervlakte van het schaalmodel in mm2 nauwkeurig.
-
Bereken de cilinderinhoud van het schaalmodel in mm3 nauwkeurig.
-
Bereken hoeveel mm3 benzine er in de tank van het schaalmodel past.
-
De spoorlijn van Arnhem naar Leeuwarden was in september 1868 geheel klaar.
De lengte van deze spoorlijn is 166 km.
Op een kaart is deze lijn 16,6 cm lang.
Wat is de schaal van die kaart?
-
Een ringslang met lengte van 1 m heeft een gewicht van 240 gram en een huidoppervlakte van 483 cm2.
Een boa constrictor is een slang die veel groter is. Een bepaalde boa weegt 51,84 kg.
Hoe groot is de huidoppervlakte van deze boa?
-
De Maan past ongeveer 64 keer in de Aarde. (Het volume van de Aarde is dus ongeveer 64 keer dat van de Maan.)
Hoeveel keer zo groot is de diameter van de Aarde als die van de Maan?
![]() www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Meten en tekenen > Schaallijnen
www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Meten en tekenen > Schaallijnen
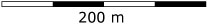 schaal 1 : ...
schaal 1 : ...
 schaal 1 : ...
schaal 1 : ...

 Hier zie je een foto van de maan.
De diameter van de maan is ongeveer 3476 km.
Hier zie je een foto van de maan.
De diameter van de maan is ongeveer 3476 km.![]() www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Meten en tekenen > Vergroten
www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Meten en tekenen > Vergroten![]() www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Meten en tekenen > Vergroten
www.math4all.nl > Havo/vwo > havo/vwo 1/2 > Meten en tekenen > Vergroten Bij een schaalmodel van een voorwerp worden alle lengtes met een vaste vergrotingsfactor verkleind. Dit model van een Smart ForTwo heeft een schaal van 1 : 18.
Bij een schaalmodel van een voorwerp worden alle lengtes met een vaste vergrotingsfactor verkleind. Dit model van een Smart ForTwo heeft een schaal van 1 : 18.