De caleidocyclus
Een praktische opdracht voor de tweede fase havo/vwo, wiskunde B
| Bronnen: |
De math4all-site voor de wiskundetheorie.
Formule-overzichten zoals je Binas, het Polytechnisch zakboekje, e.d.
Het boek 'De caleidocyclus' van Wallace Walker en Doris Schattschneider. |
| Theorie: |
Meetkunde: Inhoud van lichamen berekenen
Wiskundeboek voor de eerste fase havo/vwo |
| Resultaat: |
Leesbare uitwerking gemaakt in een tekstverwerker (titelblad leesbare uitwerking downloaden) |
| Studielast: |
8 - 10 uur |
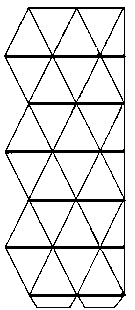
De caleidocyclus bestaat uit viervlakken die aan elkaar zitten als een ring (het griekse woord kyklos betekent ook ring). Behalve dat er een mooie vorm ontstaat (Grieks: kalos (= mooi), eidos (= vorm)), kun je ook de ring van viervlakken draaien door het midden.
Je ziet hier een mogelijke bouwplaat, waarbij er zes viervlakken ontstaan.
- Teken zelf zo'n bouwplaat. Hij bestaat uit allemaal gelijkbenige driehoeken zoals je ziet. Bijvoorbeeld kun je driehoeken nemen met een basis van 6 cm en een hoogte van 8 cm.
- Knip daarna de bouwplaat uit en vouw hem langs alle getrokken lijnen. De horizontale lijnen worden dalvouwen (dus naar je toe vouwen) en de schuine lijnen worden bergvouwen (dus van je af vouwen).
- Plak hem daarna in elkaar. Het lijkt gemakkelijker dan het is: puzzel er maar eens eventjes aan.
- Het is mogelijk de hoogte van de driehoek te variŽren als je de basis 6 cm houdt. Maar hij kan niet veel kleiner worden gemaakt. Onderzoek wat voor gevolg het variŽren van de hoogte voor de caleidocyclus heeft. Bereken ook de minimaal mogelijke hoogte als je gelijkbenige driehoeken neemt met een basis van 6 cm. Maak een bouwplaat van de ideale caleidocyclus van zes viervlakken.
- Bereken de totale inhoud van die ideale caleidocyclus.
- Onderzoek ook of je caleidocycli kunt maken met meer dan zes viervlakken. Leg uit aan welke voorwaarden de bouwplaat dan moet voldoen om een goed draaiende caleidocyclus te krijgen.
- Onderzoek of je ook niet gelijkbenige driehoeken kunt gebruiken voor de bouwplaat. Leg uit wat voor gevolgen dat heeft voor de caleidocyclus en aan welke voorwaarden er moet worden voldaan.
Maak een bouwplaat van zo'n caleidocyclus.
- Zoek het boek 'De caleidocyclus' van Wallace Walker en Doris Schattschneider op. Zij hebben Escher-patronen op caleidocycli gemaakt. Maak op jouw bouwplaten ook mooie symmetrische patronen.
Het eindresultaat wordt een leesbare uitwerking met daarin minstens twee bouwplaten en een duidelijke uitwerking van de overige opdrachten. Elke willekeurige lezer moet begrijpen wat je bedoelt.
Uitwerking:
- De twee bouwplaten. (10 punten)
- Uitleg van de vorm van de ideale caleidocyclus (met zes viervlakken) met de bijbehorende berekeningen. (10 punten)
- Berekening van de inhoud van de ideale caleidocyclus (met zes viervlakken). (10 punten)
- Voorwaarden waaraan caleidocycli van meer dan zes viervlakken moeten voldoen. (10 punten)
- Voorbeelden van 'scheve' caleidocycli. (10 punten)
- Patronen op beide bouwplaten. (10 punten)
- Maak van dit alles een leesbare uitwerking met twee keurig getekende bouwplaten (het gebruik van tekenprogramma's als Paint, CorelDraw, e.d., is toegestaan).
 Math4all
Math4all
