Totaalbeeld

Samenvatten

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Getaltheorie > Soorten Getallen > Totaalbeeld > Samenvatten

Je hebt nu het onderwerp Soorten Getallen doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!

Begrippenlijst:

11. natuurlijk getal — geheel deel — tegenstelde — deelbaar — even/oneven getal — priemgetal
12. breuk — rationaal getal — staartdeling — decimaal getal
13. vermoeden — bewijs — stelling — direct/indirect bewijs — tegenvoorbeeld — bewijs uit het ongerijmde — implicatie — equivalentie — gelijkwaardige beweringen
14. wortel — reëel getal
15. de bewijsmethode van de volledige inductie

Activiteitenlijst:

11. natuurlijke en gehele getallen herkennen — schrijfwijzen bij verzamelingen gebruiken — ontbinden in priemfactoren
12. rekenen met breuken — rationale getallen herkennen — een breuk omzetten naar een decimaal getal en omgekeerd
13. kennismaken met bewijzen, zowel directe als indirecte bewijzen
14. bewijzen dat een wortel soms geen rationaal getal is — werken met reële getallen
15. de bewijsmethode van de volledige inductie gebruiken

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Getaltheorie > Soorten Getallen > Totaalbeeld > Achtergronden

Testen

Opgaven

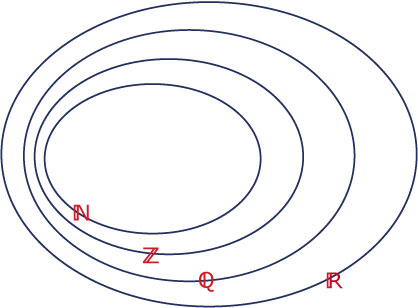
1. Je ziet hier een diagram waarin de verzamelingen van de natuurlijke getallen, de gehele getallen, de rationale getallen en de reële getallen zijn aangegeven.
   1. Zet de volgende getallen in dit diagram: `0`, `- 1/3`, `pi - 1`, `- 18/3`, `sqrt(1 5/9)`, `sqrt(1 7/9)`, `sqrt(196)`.
   2. Het getal i is de oplossing van de vergelijking `x^2 = -1`. Waar moet je i in dit diagram plaatsen?


2. Bereken de GGD en de KGV van de getallen 13464 en 46035.
   Schrijf de getallen daartoe eerst als het product van priemgetallen.
   


3. Bij breuken waarvan de noemer priem is het vaak nogal wat werk om ze als (exact) decimaal getal te schrijven.
   1. Schrijf `5/41` als decimaal getal.
   2. Schrijf 0,538461 als breuk.


4. Bekijk het getal `sqrt(6)`.
   1. Dit getal is het product van de twee irrationale getallen `sqrt(2)` en `sqrt(3)`. Mag je op grond daarvan concluderen dat `sqrt(6)` irrationaal is?
   2. Bewijs de irrationaliteit van `sqrt(6)`.


5. Schrijf de volgende getallen in de vorm `a + b sqrt(6)`:
   1. `(1 + sqrt(6))^2`
   2. `sqrt(54) - sqrt(24) + sqrt(36)`
   3. `(3 - 2sqrt(6))/(sqrt(150))`


6. Bewijs dat ⁵log(7) een irrationaal getal is.
   


7. Bewijs met behulp van volledige inductie dat `1 + 3 + 3^2 + 3^3 + ... + 3^n = 1/2 * (3^(n + 1) - 1)`.
   

Toepassen

8. Hoppen op de getallenlijn

   Je kunt als een soort kangoeroe over de getallenlijn hoppen. Je maakt bijvoorbeeld altijd sprongen van 60 of van 72 eenheden. Als je wilt weten op welke plekken je dan allemaal kunt komen, dan moet je de GGD van deze getallen zoeken. Bekijk

   www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Getaltheorie > Soorten Getallen > Totaalbeeld > Toepassen

   
   
   1. Hoeveel bedraagt de GGD van 60 en 72? Bepaal je antwoord eerst door ontbinden in priemfactoren.
   2. Bereken GGD(60,72) ook met het algoritme van Euclides.
   3. Op welke plekken op de getallenlijn kun je allemaal komen?
   4. Wanneer je altijd sprongen maakt van lengte `p` of lengte `q` met `p` en `q` allebei priem, kun je alle plaatsen van de getallenlijn bereiken. Leg uit waarom dat zo is.



9. Modulair rekenen

   Een voorbeeld van modulair rekenen is klokrekenen met gehele urenaantallen: als je bij 9 uur 5 uur optelt, krijg je 14 uur, maar op de klok is dat weer 2 uur. Dat komt omdat je alleen rekent met de twaalf getallen 0, 1, 2, 3, ..., 10, 11. Zodra je bij 12 bent is dat weer 0, etc.
   Je zegt wel `12 -= 0 (mod.12)`. Uitspraak: "12 komt overeen met 0 modulo 12".
   1. Noem nog drie getallen die overeen komen met 0 (mod.12).
   2. Waarom komen alle getallen van de vorm `3 + k * 12` met `k in ZZ` overeen met `3 (mod.12)`?
   Alle getallen die overeen komen met 3 (mod.12) vormen de restklasse `bar(3)`.
   3. Welke getallen vormen de restklasse `bar(4)`?
   4. Je kunt `1314 + 967 (mod.12)` en `1314 * 967 (mod.12)` op twee manieren berekenen: eerst de optelling / vermenigvuldiging uitvoeren en dan veelvouden van 12 weglaten of eerst veelvouden van 12 weglaten bij de afzonderlijke getallen 1314 en 967 en de bewerking uitvoeren. Toon aan dat dit geen verschil maakt.
   5. Bewijs dat `a +- b (mod.m) = a (mod.m) +- b (mod.m)` en `a + b (mod.m) = a (mod.m) + b (mod.m)`.
   Delen is bij restklassen een heel ander verhaal. Je komt dit bijvoorbeeld tegen bij het oplossen van eenvoudige vergelijkingen.
   6. Los op: `x + 5 = 2 (mod.12)`.
   7. Los op: `7x = 3 (mod.12)`.
   8. Welk probleem doet zich voor als je `2x = 3 (mod.12)` wilt opossen?
   In de moderne cryptografie (geheimschrift schrijven) wordt van het rekenen met restklassen gebruik gemaakt. Alle symbolen worden dan omgezet naar hun bijbehorende ASCII-code, naar tweecijferige decimale getallen. Vervolgens kun je elk symbool versleutelen naar bijvoorbeeld `f(x) = 12 * x + 34`(mod.97) waarin `x` de tweecijferige ASCII-code van het symbool voorstelt en `f` de zogenaamde encryptiefunctie is. Door mod.97 te werken gebruik je alleen de eerste 97 ASCII-tekens.
   9. Versleutel zo het woord WISKUNDE.
   10. Hoe kun je het vanuit het versleutelde woord de oorspronkelijke tekst weer terugvinden? Gaat dat gemakkelijk?
   Hoewel het voorgaande rekenwerk met een rekenmachine nog best lastig is, is het eenvoudig te programmeren en dus totaal ongeschikt voor echte geheime code. Daarvoor bestaan ingewikkelder procedures, die wel met modulorekenen te maken hebben...
   



10. Het vermoeden van Goldbach en andere openstaande kwesties

    Bekijk via

    www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Getaltheorie > Soorten Getallen > Totaalbeeld > Toepassen

    
    wat het vermoeden van Goldbach is. Het is in ieder geval één van de vermoedens in de wiskunde die nog openstaan voor een bewijs, dus voel je uitgedaagd!
    1. Laat zien dat het vermoeden van Goldbach geldt voor de getallen 48 en 76. Probeer zelf nog maar een paar andere getallen.
    2. Waarom is het onmogelijk (ook als je veel helpers zou hebben met snelle computers voor het rekenwerk) om de stelling op deze manier te bewijzen?
    3. Zoek nog één of twee openstaande vraagstukken in de wiskunde en probeer er meer informatie over te verzamelen. Leg dit vast in een voor jou begrijpelijke tekst.