Totaalbeeld

Antwoorden bij de opgaven

1. 1. Kwadraat afsplitsen geeft `((x-3)^2)/13 + ((y+1)^2)/(3,25) = 1`.
      Hierin is `13 = (0,5r)^2` en `3,25 = (0,5r)^2 - p^2`, zodat `p = +-sqrt(9,75)`. De brandpunten zijn daarom `(3 - sqrt(9,75); -1)` en `(3 + sqrt(9,75); -1)`. De symmetrieassen zijn `x = 3` en `y = -1`.
   2. De vergelijking van de kromme is `y = 1/16 x^2 + 4`, dus dit is een parabool met de `y`-as als symmetrieas en top `(0,4)`.
   3. Na kwadraat afsplitsen `(x-3)^2 = y^2 - (z-2)^2`, ofwel `(x-3)^2 + (z-2)^2 = y^2`.
      Dit is een kegel met top `(3,0,5)` en een as evenwijdig aan de `y`-as. Voor de halve tophoek `phi` geldt `tan^2(phi) = 1`. De halve tophoek is daarom `phi = 1/4 pi`.
   4. Vergelijking `((y-3)/4)2 + ((z+5)/4)^2 = 1`, dus `(y-3)^2 + (z+5)^2 = 16`. Dus dit is een cilinder met as evenwijdig aan de `x`-as en door `(0,3,-5)`. De straal van de cilinder is `4`.
2. 1. Voor elk punt `P(x,y)` op `k` geldt: `|OP| + |PA| = 5`.
      Dus `sqrt(x^2 + y^2) + sqrt((4 - x)^2 + y^2) = 5` en dit geeft `36(x - 2)^2 + 100y^2 = 225` ofwel `((x - 2)^2)/(2,5^2) + (y^2)/(1,5^2) = 1`. Dus `k` is een ellips.
   2. Gebruik `cos^2(t) + sin^2(t) = 1`. Een p.v. is bijvoorbeeld `x = 2 + 2,5 cos(t) ^^ y = 1,5 sin(t)`.
   3. `(text(d)y)/(text(d)x) = (1,5 cos(t))/(-2,5 sin(t)) = 1` geeft `tan(t) = - 5/3` en dus `t ~~ 2,11 vv t ~~ 5,25`. Even invullen in de p.v. geeft `(3,29; -1,29)` en `(0,71; 1,29)`.
   4. Lijnen door `B(7,0)` met richtingscoëfficiënt `a` hebben een vergelijking zoals `y = ax - 7a`.
      Deze lijnen snijdt je met de ellips (invullen in de vergelijking) en je eist `D = 0` vanwege het raken. Je vindt ongeveer `y = -0,35x + 2,42` en `y = 0,35x - 2,42`.
3. 1. Even herleiden tot `c: (x - 3)^2 + y^2 = 5` en `p: y^2 = -0,5(x - 3)`.
      Het middelpunt van `c` is `M(3,0)` en de top van de parabool is `T(3,0)`.
   2. De afstand van brandpunt tot richtlijn is `0,25` en het brandpunt ligt links van de top (vanwege het minteken van `-0,5`). Dus brandpunt van `p` is `F(2,875;0)` en de richtlijn is `x = 3,125`.
   3. Snijpunten vindt je uit `(x - 3)^2 - 0,5(x - 3) = 5` en dit geeft `x = +-1` en dus zijn de snijpunten `A(1,1)` en `B(-1,-1)`. Neem `A(1,1)` en bepaal de richtingscoëfficiënten van de raaklijnen aan beide krommen in dit punt. Voor `c` geldt (impliciet differentiëren): `(text(d)y)/(text(d)x) = (-2x + 6)/(2y)` en dus is de r.c. van de raaklijn in `A` aan `c` gelijk aan `2`. Voor `p` geldt: `(text(d)y)/(text(d)x) = (-0,5)/(2y)` en dus is de r.c. van de raaklijn in `A` aan `c` gelijk aan `-0,25`. De hoek tussen beide kun je bijvoorbeeld met het inproduct van de bijbehorende richtingsvectoren berekenen. Je vindt ongeveer `67,4`°.
   4. Dat is de boog tussen beide snijpunten. Daarbij hoort een middelpuntshoek van `53,2`°. De lengte van die boog is `(53,2)/(360) * 2pi * sqrt5 ~~ 2,08`.
4. 
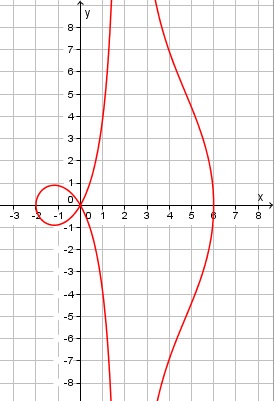
   1. Schrijf de vergelijking als `y^2 = (16x^2)/((x-2)^2) - x^2`.
      Je ziet dan dat `x != 2` en verder dat `(16x^2)/((x-2)^2) - x^2 >= 0`. Dit is alleen het geval als `-2 <= x <= 6 ^^ x != 2`. De `y`-waarden kunnen alle reële waarden aannemen. Zie de figuur hiernaast.
   2. Op de `x`-as is `y = 0` en dit geeft de punten `(-2,0)`, `(0,0)` en `(6,0)`.
      Op de `y`-as is `x = 0` en dit geeft het punt `(0,0)`.
   3. In dat geval heeft de afgeleide geen reële waarde, maar gaat naar oneindig.
      `(text(d)y)/(text(d)x) = (-64x)/(2y(x-2)^3) - (x)/(y)` bestaat niet als `x = 2 vv y = 0`. Dat levert de punten `(-2,0)` en `(6,0)` op, want in `(0,0)` is de afgeleide onbepaald en `x=2` geeft geen punt van de kromme.
   4. `(text(d)y)/(text(d)x)` is in `(0,0)` niet te bepalen. Maar je kunt wel werken met een lijn van de vorm `y = px`. Die kun je snijden met de kromme. Je krijgt dan `p^2x^2 = (16x^2)/((x-2)^2) - x^2` en dus `x^2((1-p^2)(x-2)^2 - 16) = 0`. Bij raaklijnen mag dit alleen `x=0` opleveren, dus `1 - p^2 = 0`, ofwel `p = +-1`. De raaklijnen maken daarom een hoek van `90`°.
5. 1. Middelpunt `M(4,3,0)` en straal `r=5`.
   2. `(x - 4)^2 + (y - 3)^2 + z^2 = 25`
   3. Op de `x`-as is `y=0 ^^ z=0`, dus `(x - 4)^2 = 16`. Dat geeft `(0,0,0)` en `(8,0,0)`.
      Op de `y`-as is `x=0 ^^ z=0`, dus `(y - 3)^2 = 9`. Dat geeft `(0,0,0)` en `(0,6,0)`.
      Op de `z`-as is `x=0 ^^ y=0`, dus `z^2 = 0`. Dat geeft `(0,0,0)`.
   4. Dit kun je op verschillende manieren aanpakken: meetkundig (met de SvP) of algebraïsch (`z = 2,5` invullen in de bolvergelijking). Je krijgt een straal van `sqrt(25 - 2,5^2)`.
   5. Voor de halve tophoek `phi` van de kegel geldt: `tan(phi) = (sqrt(25 - 2,5^2))/(2,5) = sqrt3`. De vergelijking is daarom `(x - 4)^2 + (y - 3)^2 = 3z^2`.
   6. Teken een doorsnede van bol en kegel en het vlak `x = 4`. De doorsnede van de bol en dit vlak is een cirkel met vergelijkingen `(y - 3)^2 + z^2 = 25 ^^ x=4`. De doorsnede van de kegel en dit vlak bestaat uit twee lijnen door het middelpunt van de bol (en dus van de cirkel) en het raakpunt. Het raakvlak aan de kegel zie je dan als straal van de bol (en dus van de cirkel) naar het raakpunt en het raakvlak aan de kegel zie je als raaklijn aan de cirkel in het raakpunt. Deze staan loodrecht op elkaar, dus de hoek tussen kegel en bol is ook `90`°.
   7. `P(4,6,4)` ligt op de bol en `l` maakt dus een hoek van `60`° met de normaalvector van het raakvlak in `P`. Die normaalvector is `MP = ((0),(3),(4))`. Verder staat `l` loodrecht op de normaalvector van het vlak `x = y`. Die normaalvector is `((1),(-1),(0))`.
      Neem je nu voor de richtingsvector van `l` de vector `((1),(a),(b))`, dan volgt uit beide inproducten `3a + 4b = 0,5 * 5 * sqrt(1 + a^2 + b^2) ^^ 1 - a = 0`. Dit levert op: `a = 1 ^^ b = (-48 +- sqrt(2990))/49`. Je vindt twee mogelijke parametervoorstellingen, namelijk:
      `((x),(y),(z)) = ((4),(6),(4)) + t * ((1),(1),(0,14))` en `((x),(y),(z)) = ((4),(6),(4)) + t * ((1),(1),(-2,10))`
10. 1. Op de `x`-as is `y=0` en dus `t^2 + t + 0,25 = 0` zodat `t = -0,5`. Het snijpunt is `(-1,25;0)`.
       Op de `y`-as is `x=0` en dus `t^2 - t - 2 = 0` zodat `t = -1 vv t = 2`. De snijpunten zijn `(0;0,25)` en `(0;6,25)`.
    2. `(text(d)y)/(text(d)x) = (2t + 1)/(2t - 1)`
       Op de `x`-as is `y'=0 ^^ x'!=0` en dus `t = -0,5`. Het bijbehorende punt is `(-1,25;0)`.
       Op de `y`-as is `x'=0 ^^ y'!=0` en dus `t = 0,5`. Het bijbehorende punt is `(-2,25;1)`.
       
    3. Voor `A` geldt `t = -1` en dus `(text(d)y)/(text(d)x) = 1/3`.
       Voor `B` geldt `t = 2` en dus `(text(d)y)/(text(d)x) = 5/3`.
       De gevraagde hoek bereken je daarom met het inproduct van `((3),(1))` en `((3),(5))`. Die hoek wordt ongeveer `41`°.
    4. `x + y = p` snijden met de parabool: `2t^2 - 1,75 = p`. Je krijgt precies één waarde van `t` als `p = -1,75`.
    5. De symmetrieas is de middelloodlijn van de lijn door `(-2,25;1)` en `(-1,25;0)`.
       Hij heeft daarom als vergelijking `y = x + 2,25`.
11. 1. Bol `beta` raakt `OC` in `O` dus het middelpunt `M` ligt in vlak `OAED`. Verder ligt `M` evenver van `O`, `F` en `B`. Dus is `M` het midden van `AE` en is de straal van de bol `sqrt(6^2 + 3^2) = sqrt45`. De vergelijking van `beta` is `(x - 6)^2 + y^2 + (z - 3)^2 = 45`.
    2. Bol `gamma` heeft vergelijking `(x - 6)^2 + (y - 3)^2 + z^2 = 45`.
       Lijn `EG` heeft v.v. `((x),(y),(z)) = ((6),(0),(6)) + t * ((6),(-6),(0))`.
       Voor de snijpunten van `gamma` en `EG` vind je `t = 0 vv t = -0,5`. Het zijn dus `E(6,0,6)` en `H(3,3,6)`. En `|EH| = 3sqrt2`.
    3. Punt `R` ligt op de raaklijn vanuit `B` aan de snijcirkel van de cilinder met vlak `ABFE`. Het raakpunt is `P`. Nu is `AP = 3` en `AB = 6` en `/_ APB = 90`°, dus `BP = 3sqrt3`. Ook is `/_ ABP = 30`°. Verder is `Delta BCR` gelijkvormig met `Delta PBA` (hh) en dus is `BR = 6/(3sqrt3) * 3 = 2sqrt3`. Hieruit kun je de coördinaten van `R` berekenen: `z_R = sqrt3`, `y_R = 3` en `x_R = 6` (maar dat wist je al). Dus `R(6,3,sqrt3)`.