Bol en cilinder

Antwoorden bij de opgaven

1. 1. Controleer de afstand van elk punt tot `O`, die moet `3` zijn. Dit geldt alleen voor `A`, `B`, `C` en `E`.
   2. `sqrt(a^2 + a^2 + a^2) = 3` geeft `a = +-sqrt3`.
   3. Als `-sqrt3 < a < sqrt3`.
   4. `x^2 + y^2 + z^2 = 9`
   5. Met `z=0`: `x^2 + y^2 = 9` is een cirkel in dit vlak met straal `3`.
      Met `z=1`: `x^2 + y^2 = 8` is een cirkel in dit vlak met straal `2sqrt2`.
      Met `z=2`: `x^2 + y^2 = 5` is een cirkel in dit vlak met straal `sqrt5`.
      Met `z=3`: `x^2 + y^2 = 0` is een cirkel in dit vlak met straal `0`, dus gewoon het punt `O`.
   6. `y = -z` geeft `x^2 + 2z^2 = 9`. Dit lijkt een ellips, maar pas op met 3D: het is een cirkel in het vlak `y=-z`.
2. 1. Doen.
   2. Alweer een cirkel met straal `3`, maar nu iets hoger.
   3. Steeds een cirkel met straal `3`, maar op verschillende hoogtes.
   4. Voor elk punt op de cilinder geldt `x^2 + y^2 = 9`.
   5. `y^2 + z^2 = 16`
3. 1. `M(1,4,0)` en `r = 5`.
   2. `(x + 2)^2 + (y - 1)^2 + (z - 2)^2 = 6`
   3. `(x - 1)^2 + (z - 3)^2 = 10`
4. 1. Omdat de normaalvector van een raakvlak in `P` de vector `MP` is (`M` is daarin het bolmiddelpunt).
   2. Doe zelf dit voorbeeld even uitgebreid.
   3. Kwadraat afsplitsen geeft `(x - 4)^2 + y^2 = 29`. Dit is een cilinder met een as evenwijdig aan de `z`-as en door `(4,0,0)` en straal `sqrt(29)`.
   4. Eerst checken of `Q(2,5,3)` op de cilinder ligt, dat is het geval!
      Normaalvector raakvlak (bovenaanzicht bekijken/tekenen) is `((2),(-5),(0))`, dus vergelijking vlak `2x - 5y = -21`.
   5. Dat raakvlak gaat door `R(4,-5,3)`, dus vergelijking `2x - 5y = 33`.
   6. Bijvoorbeeld als `(x,y) = (at, 2 + t)` raakt aan `x^2 + y^2 = 8x + 13`, dus als `a^2t^2 + (t+2)^2 = 8at + 13` één oplossing voor `t` heeft. Dit betekent `D = (4 - 8a)^2 + 36(a^2 + 1) = 0` en dus `100a^2 - 64a + 52 = 0`.
5. 1. `(3 cos(u))^2 + (3 sin(u))^2 = 9 (cos^2(u) + sin^2(u)) = 9` en dat klopt.
   2. Een schroeflijn over het cilinderoppervlak, want bij toenemende `u` draait niet alleen het punt, maar het gaat tegelijk ook omhoog.
   3. Zowel `u` als `v` lopen bijvoorbeeld van `0` tot `2pi`.
   4. `|OP| = r` en `|OQ| = r cos(v)` en hieruit volgt `x = +-|OR| = r cos(u) cos(v)` en `y = r sin(u) cos(v)`. De `z`-waarde is `z = +-|PQ| = r sin(u)`.
   5. Invullen en gebruik maken van `sin^2(x) + cos^2(x) = 1`.
6. 1. `x^2 + z^2 = 34`
   2. Bereken eerst de afstand van `O` tot `V: x + y + z = 6`: `text(d)(O,V) = 2sqrt(3)` (loodlijn opstellen, snijden met het vlak, afstand `O` tot snijpunt opstellen). De vergelijking van de cirkel is dus `x^2 + y^2 + z^2 = 18`.
   3. `(x - 4)^2 + (y - 4)^2 = 16`
   4. Het middelpunt is `(1,1,1)` en de straal is `sqrt(3)`, dus de vergelijking is `(x-1)^2 + (y-1)^2 + (z-1)^2 = 3`.
7. 1. Doen. In het `xy`-vlak krijg je `(x^2)/4 + (y^2)/16 = 1` (een ellips). In het `yz`-vlak krijg je `(y^2)/16 + (z^2)/4 = 1` (een ellips). In het `xz`-vlak krijg je `x^2 + y^2 = 4` (een cirkel met straal `2`).
   2. Zie a.
   3. Laat zien dat als `(a,b,c)` op de ellipsoïde dan ook `(a,-b,c)` op de ellipsoïde.
   4. `x = sqrt(4-t^2) cos(u)`, `y = 2t` en `z = sqrt(4-t^2) sin(u)`.
   5. `9x^2 + 9y^2 + z^2 = 36` en de parametervoorstelling is `x = sqrt(4-4t^2)cos(u) ^^ y = sqrt(4-4t^2)sin(u) ^^ z=6t`.
8. 1. Bol, even kwadraat afsplitsen: `(x-0,5)^2 + (y-0,5)^2 + (z-1)^2 = 0,25`, dus `M(0,5;-0,5;1)` en `r=0,5`.
   2. Cilinder met straal `2` en as door `(0,3,4)` en evenwijdig aan de `x-as`.
   3. Cilinder, even kwadraat afsplitsen: `(x-6)^2 + y^2 = 36`. Dus straal `6` en een as evenwijdig aan de `z`-as door `(6,0,0)`.
   4. Bol met straal `5` en `M(5,5,0)`.
9. 
   1. Doen, de bol heeft middelpunt `O(0,0,0)` en straal `2`.
   2. Middelpunt is `G(0,4,4)` en de straal is `sqrt(32)-2`. Dus de vergelijking is `x^2 + (y-4)^2 + (z-4)^2 = (sqrt(32)-2)^2`.
   3. Middelpunt is `M(2,2,2)` en de straal is `2sqrt(3)`. Dus de vergelijking is `(x-2)^2 + (y-2)^2 + (z-2)^2 = 12`.
   4. `(x-4)^2 + (y-4)^2 = 9`
   5. `sqrt(32)-2-3 = 4sqrt(2) - 5` (bovenaanzicht maken).
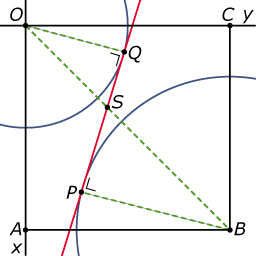
   6. Dit vraagt om een meetkundige oplossing. Hier zie je een bovenaanzicht, het gaat om de lengte van `PQ`. Je ziet dat `|BP|=3` en `|OQ|=2`. Verder is `|OB|=4sqrt2`. Omdat de twee driehoeken `BPS` en `OQS` gelijkvormig zijn, kun je berekenen dat `|BS|=2,4sqrt2` en `|OS| = 1,6sqrt2`. Hiermee kun je `|PS|` en `|QS|` berekenen. Dus `|PQ| = sqrt(2,52) + sqrt(1,12)`.
10. 1. `M(3,3,3)` en `r = sqrt27` geeft vergelijking `(x-3)^2 + (y-3)^2 + (z-3)^2 = 27`.
    2. De bol moet raken aan het vlak `ABC`.
       `M(p,p,p)` en `|OM| = 1/2 * d(O,ABC) = sqrt(3)`, dus `3p^2=3` en `p=1`.
       Middelpunt `M(1,1,1)` en straal `sqrt3` geeft `(x-1)^2 + (y-1)^2 + (z-1)^2 = 3`.
11. 1. Middelpunt `M(4,3,2)` en straal `r=3` geeft `(x-4)^2 + (y-3)^2 + (z-2)^2 = 9`.
    2. Neem in de vergelijking `z=4` en je vindt `(x-4)^2 + (y-3)^2 = 5`. Dit is een cirkel met straal `sqrt5`. Hierbij is `2 + 3 sin(v) = 4` en dus `v = arcsin(2/3) ~~ 0,730 vv v = pi - arcsin(2/3) ~~ 2,412`.
    3. `v=0` geeft `(x,y,z) = (4 + 3 cos(u), 3 + 3 sin(u), 2)`.
       Je hebt hier te maken met een cirkel in het vlak `z=2` en vergelijking `(x-4)^2 + (y-3)^2 = 9`. Dit is ook de vergelijking van de cilinder met as evenwijdig aan de `z`-as die precies om de bol past.
    4. Het raakpunt is `P(4 + 1,5 sqrt2; 3 + 1,5 sqrt2; 2)`. De normaalvector van het raakvlak is `vec(PM) = ((1,5 sqrt2),(1,5 sqrt2),(0))`. Dus het vlak heeft vergelijking `1,5x sqrt2 + 1,5y sqrt2 = 10,5 sqrt2 + 9` (coördinaten van `P` invullen).
    5. `x = 2 + 4t ^^ y = 1 + 4t ^^ z = 3` invullen in de bolvergelijking geeft `t = 0 vv t = 1`. Dus `A(2,1,3)` en `B(6,5,3)`.
       Het raakvlak in `A` heeft normaalvector `((2),(2),(-1))` en het raakvlak in `B` heeft normaalvector `((2),(2),(1))`. De hoek tussen beide vlakken is gelijk aan de hoek tussen beide normaalvectoren. En die bereken je met behulp van het inproduct. Je vindt `arccos(7/9) ~~ 39`°.
12. 1. Teken een aanzicht van de cilinder in de richting van de as. Daarin zie je een cirkel met lijnstuk `AB'`, waarin `B'` de loodrechte projectie van `B` op vlak `V` is. Daarin is `|AB'| = sqrt(4^2 - 2^2) = 2 sqrt3`.
       Is `M` het midden van de cirkel in het aanzicht en `N` het midden van `AB'`, dan is de straal `|MA| = sqrt((sqrt3)^2 + 1^2) = 2`.
    2. Ook dit moet je via het aanzicht meetkundig oplossen. De bedoelde raakvlakken zie je dan als raaklijnen aan de cirkel die loodrecht staan op de stralen `MA` en `MB'`. De gevraagde hoek is `180° - /_AMB'` en met goniometrie kun je `/_AMB' = 120`° berekenen. De hoek tussen beide raakvlakken is `60`°.
13. 1. Vergelijking herleiden tot `(x - 2)^2 + (z + 2)^2 = 8` geeft een cilinder met as evenwijdig aan de `y`-as door `M(2,0,-2)` en straal `sqrt8`.
    2. Bol met middelpunt `M(0,0,4)` en straal `2`.
    3. Vergelijking herleiden tot `x^2 + (y-5)^2 + (z+3)^2 = -5` dus dit is niks, een bol met straal `sqrt(-5)` kan niet. (Imaginaire bol???)
    4. Cilinder met as evenwijdig aan de `z`-as door `(5,5,0)` en een straal van `5`.
14. 1. Teken een aanzicht in de richting van de `x`-as, je ziet dan driehoek `ACT` waarin het snijpunt van de middelloodlijnen het middelpunt `M` van de bol is. Dit snijpunt kun je bereken met goniometrie, of met vergelijkingen van de middelloodlijnen.
       Je vindt `M(0,3,0)` en een straal van `|MT| = 5`. De vergelijking van de bol is `x^2 + (y-3)^2 + z^2 = 25`.
    2. In snijpunt `A` is de normaalvector van het raakvlak `((0),(-3),(4))` en de richtingsvector van lijn `AT` is `((0),(8),(-4))`. De hoek hiertussen is `arccos(2/(sqrt5)) ~~ 27`°. De gevraagde hoek is daarom ongeveer `90° - 27° = 63°`.
    3. `x^2 + y^2 = (2 sqrt2)^2 = 8`
    4. Hier kan een analytische oplossing (vectorvoorstelling `BT` invullen in vergelijking cilinder en zo `P` berekenen). Hier kan ook een meetkundige oplossing (in een bovenaanzicht werken met verhoudingen). Je vindt `P(2 sqrt2, 8 - 4 sqrt2, 0)`. En dus is `|OP| = sqrt((2 sqrt2)^2 + (8 - 4 sqrt2)^2 + 0^2) = sqrt(104 - 64 sqrt2)`.