3D krommen

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Krommen en oppervlakken > 3D krommen > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.
Kijk je van boven op het `Oxy`-vlak, dan kun je de `z`-waarde buiten beschouwing laten. Welke kromme zie je dan?
Daarna vraag je je af wat de `z`-functie met het hoogteverschil doet.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Krommen en oppervlakken > 3D krommen > Uitleg

Lees eerst de Uitleg goed door. Bekijk de animatie, draai de figuur met de rechter muisknop.

1. Bekijk de Uitleg. Construeer door het groene bolletje over de cirkel te bewegen een stukje van een (Archimedische) schroeflijn.
   1. Maak om te beginnen een tabel met waarden voor `x`, `y` en `z` als `t = 0, 1/4pi, 1/2pi, pi, ..., 2pi`.
   2. Teken vervolgens een ruimtelijk `xyz`-assenstelsel met de punten uit je tabel er in. Probeer nu zelf de schroeflijn te tekenen.
   3. Bekijk van boven (dus langs de `z`-as naar beneden) op de schroeflijn. Wat zie je?
   4. Kijk je van boven, dan speelt de `z`-waarde geen rol. Laat zien dat de kromme dan een cirkel is en stel een vergelijking van die cirkel op.
   5. Kijk nu langs de `y`-as naar de kromme. Wat zie je?
   6. Bij kijken langs de `y`-as speelt de `y`-waarde geen rol. Nu is `x` een functie van `z`. Welke functievoorschrift hoort daar bij?
   7. Beschrijf zo ook met een formule de kromme die je zit als je langs de `x`-as kijkt.


2. Bekijk de schroeflijn uit de voorgaande opgave nog eens.
   1. Hoe kun je het snijpunt van deze kromme met het vlak `z = 2` berekenen?
   2. Bereken de snijpunten van de schroeflijn met het vlak `x = y`. Waarom zijn het er oneindig veel?


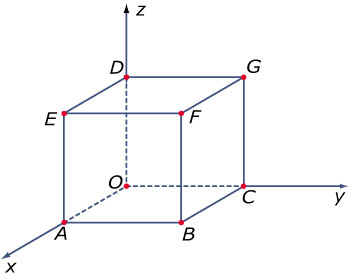3. Een rechte lijn `l` heeft vectorvoorstelling `((x),(y),(z)) = ((0),(2),(4)) + t * ((3),(2),(1))`.
   1. Welke parametervoorstelling heeft deze lijn?.
   2. Teken `l` in een assenstelsel met een kubus met ribben van 6 (zie figuur hiernaast).
   3. In welke punten snijdt `l` de kubus?
   Stel je voor dat de beweging van punt `P` in het assenstelsel beschreven wordt door deze rechte lijn. `t` is de tijd in seconden.
   4. Welke waarden kan `t` aannemen voor de punten `P` die binnen de kubus liggen?
   5. Hoe lang is het gedeelte van `l` dat binnen de kubus ligt?
   6. Hoe lang bevindt `P` zich binnen de kubus? Met welke snelheid beweegt `P`?


4. Een punt `P` beweegt met een constante snelheid en richting in een driedimensianaal rechthoekig `Oxyz`-assenstelsel. Op `t = 0` bevindt `P` zich in `(7,0,4)` en op `t = 1` in `(7,1,3)`.
   1. Waar zit `P` op `t = 10`? En op `t = -2`?
   2. Geef een parametervoorstelling van de baan van `P`.
   3. Hoe groot is de snelheid waarmee `P` beweegt?
   4. Welke vector is de snelheidsvector van `P`? Wat is het verschil tussen de snelheid en de snelheidsvector?
   5. Laat zien dat de snelheidsvector `vec v = (x'(t),y'(t),z'(t))` is.
   Een ander punt `Q` doorloopt de baan beschreven door `(x,y,z) = (5+t,6+2t,6+2t)`.
   6. Botsen deze punten op elkaar?
   7. Hebben de banen van deze punten een snijpunt?

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Krommen en oppervlakken > 3D krommen > Theorie

Bestudeer eerst de Theorie. In de opgaven word je naar de Theorie en naar de Voorbeelden verwezen.

Opgaven

5. In de Theorie zie je hoe een kromme (of een rechte) in de ruimte kan worden beschreven met een parametervoorstelling.
   1. Waarom kan dit in het algemeen niet met een vergelijking in `x`, `y` en `z`?
   2. Leg uit hoe je aan de parametervoorstelling in Voorbeeld 1 ziet dat de figuur die je in de applet kunt construeren een schroeflijn is.
   3. In dit voorbeeld wordt de lengte van deze schroeflijn berekend. Loop deze berekening na.
   In dit voorbeeld wodt ook verteld wat de spoed van een schroeflijn is.
   4. Hoe ziet de parametervoorstelling er uit van een schroeflijn met dezelfde spoed die ligt op een cilinder om de `z`-as met straal 2?
   5. Hoe ziet de parametervoorstelling er uit van een schroeflijn met een twee keer zo grote spoed die ligt op een cilinder om de `z`-as met straal 2?
   6. Hoe ziet de parametervoorstelling er uit van een schroeflijn met spoed `2pi` die ligt op een cilinder om de `x`-as met straal 2?


6. In Voorbeeld 2 gaat het over de snelheid waarmee een punt op een schroeflijn beweegt.
   1. Waarom beweegt een punt over een schroeflijn altijd met een constante snelheid?
   2. Is ook de snelheidsvector constant? Waarom?
   3. Bekijk de gegeven parametervoorstelling. Hoe moet je deze parametervoorstelling aanpassen om het punt twee keer zo snel te laten bewegen?
   4. Met behulp van de snelheidsvector kun je een parametervoorstelling van de raaklijn in een punt van de schroeflijn bepalen. Stel een parametervoorstelling van de raaklijn aan de schroeflijn op in het punt `A` waarvoor geldt `x = 0,5pi`.
   5. Welke hoek maakt deze raaklijn met de `y`-as?
   6. Deze raaklijn snijdt het `xy`-vlak. In welk punt en onder welke hoek?


7. Ten opzichte van een rechthoekig `Oxyz`-assenstelsel beweegt een punt `P` over de kromme `k` met parametervoorstelling `(x,y,z) = (t,t+2,sqrt(t))`. Hierin is `t` de tijd in seconden.
   1. Op welk tijdstip zit `P` op de `y`-as? In welk punt?
   2. Bereken op welk tijdstip `P` in het vlak `z = 9` zit.
   3. Teken een bovenaanzicht van kromme `k`. (Je kijkt dan langs de `z`-as naar beneden.)
   4. Teken een vooraanzicht van kromme `k`. (Je kijkt dan langs de `x`-as naar achteren.)
   5. Stel de snelheidsvector van `k` op.
   6. Met welke snelheid beweegt `P` als dit punt door het vlak `z = 9` gaat?
   7. Onder welke hoek gaat `P` door het vlak `z = 9`?
   8. Op welk tijdstip zit `P` het dichtst bij `O`? Hoe groot is de afstand van `P` tot `O` dan?


8. De kromme waarvan je in Voorbeeld 3 een parametervoorstelling ziet is een soort achtbaan.
   1. Welke waarden kunnen `x`, `y` en `z` aannemen?
   2. Welke parametervoorstelling heeft de projectie van deze kromme op de `xy`-vlak (het bovenaanzicht dus)?
   3. Teken (in GeoGebra?) de kromme die bij deze projectie hoort.
   4. Laat zien dat de projectie een 8 is die symmetrisch is t.o.v. de oorsprong van het assenstelsel.
   5. Licht nu toe waarom hier sprake is van een achtbaan.
   6. Bereken hoogste punten van deze achtbaan en bereken de snelheid in die punten.
   7. Bereken in deze hoogste punten ook de hoek die de baan op dat moment met het horizontale `xy`-vlak maakt.
   8. Op welke momenten bereikt een punt dat deze achtbaan doorloopt zijn hoogste snelheid?

Verwerken

9. Gegeven zijn de krommen `k_1: (x,y,z) = (t+1,2t,t+3)` en `k_2: (x,y,z) = (s,s,s^2)`.
   1. Leg uit waarom `k_1` een rechte lijn is.
   2. Bereken de kortste afstand van `k_1` tot de oorsprong `O` van het assenstelsel.
   3. Bereken de hoek waaronder beide krommen elkaar snijden.
   4. Heeft `k_2` een raaklijn evenwijdig aan het `yz`-vlak? En aan het `xy`-vlak?
   5. Teken de kubus `OABC.DEFG` met `A(6,0,0)`. Teken in die kubus de delen van `k_1` en `k_2` die erbinnen liggen.
   6. `k_2` heeft twee punten met de kubus gemeen. Bereken de coördinaten van die twee punten.
   7. Hoe lang is het gedeelte van `k_1` dat binnen de kubus ligt?


10. De schroeflijn `s` is gegeven door de parametervoorstelling `(x,y,z) = (2t,4 sin(t),4 cos(t))` met `t >= 0`.
    1. Welk punt is het beginpunt van deze kromme?
    2. Welke waarden kunnen `x`, `y` en `z` aannemen?
    3. Waaraan kun je zien dat deze kromme op een cilinder ligt? Welke as heeft die cilinder?
    4. Hoe lang is elke omwenteling van de schroeflijn?
    5. Welke hoek maakt de schroeflijn met het vlak `x = 4`?
    6. Welke snelheid heeft een punt `P` dat over deze schroeflijn beweegt op het moment dat `x = 4`?


11. Gegeven is ten opzichte van een rechthoekig assenstelsel `Oxyz` de kromme `k` door `(x,y,z) = (2t,t^2-t,text(e)^t)`.
    1. Bereken de snijpunten van `k` met de coördinaatvlakken.
    2. Bereken de punten van `k` waarin de raaklijn evenwijdig is met één der coördinaatvlakken.
    3. Bereken de hoek waaronder `k` de `z`-as snijdt.


12. Twee punten bewegen in een driedimensionaal `Oxyz`-assenstelsel. `P_1` beweegt volgens een rechte lijn en met een constante snelheid. Op `t = 0` bevindt het zich in `(0,0,6)` en op `t = 1` in `(2,4,6)`.
    De baan van `P_2` wordt beschreven door `(x,y,z) = (2t,4t,t^2-0,25)`.
    ook hierin is `t` de tijd en `t >= 0`.
    1. Bereken het punt waarop beide punten tegen elkaar botsen.
    2. Hoe groot is de snelheid van `P_1` bij de botsing?
    3. En hoe groot is de snelheid van `P_2` op dat moment?
    4. Onder welke hoek botsen de punten op elkaar?



13. De konische schroeflijn

    Een voorbeeld van een konische schroeflijn is de kromme `k` gegeven door `(x,y,z) = ((4pi - t) sin(t), (4pi - t) cos(t), 2t))` met `0 <= t <= 4pi`. Een punt `P` beweegt over deze kromme, waarbij `t` de tijd in seconden voorstelt.
    1. Bereken het snijpunt van `k` met de `z`-as.
    2. Bereken de coördinaten van de snijpunten van `k` met het `yz`-vlak en teken de projectie van `k` op dat vlak (een vooraanzicht dus).
    3. Teken ook (met GeoGebra?) de projectie van `k` op het `xy`-vlak.
    4. `R` is de afstand van `P` tot de oorsprong van het assenstelsel. Stel een zo eenvoudig mogelijke formule voor `R` op.
    5. Stel een formule op voor de snelheid `v` van `P` als functie van `t`. Met welke snelheid begint `P` aan zijn beweging?
    6. Op welke tijdstippen is `v` maximaal of minimaal?
    7. Onder welke hoek met de `z`-as nadert `P` het eindpunt van zijn baan?

Testen

14. Gegeven is de schroeflijn `s` door de parametervoorstelling `(x,y,z) = (2 + 2 cos(t), 2 + 2 sin(t), t)` met `0 <= t <= 2pi`.
    1. Maak een schets van deze schroeflijn in de kubus `OABC.DEFG` waarvan `A(4,0,0)` en `D(0,0,4)` is.
    2. Bereken de snijpunten van `s` met deze kubus.
    3. Hoe lang is het deel van de schroeflijn dat binnen de kubus ligt?
    4. Onderzoek of er een punt op de schroeflijn is waarin de raaklijn evenwijdig is met lijn `OF`.


15. De punten `P` en `Q` bewegen in een rechthoekig `Oxyz`-assenstelsel.
    Voor `P` geldt: `(x,y,z) = (t;2t;0,25t^2)`.
    Voor `Q` geldt: `(x,y,z) = (t,6+t,3+t)`.
    Hierin is `t` de tijd in seconden. Beide punten starten op `t = 0` maar op verschillende plaatsen. Na verloop van tijd botsen ze op elkaar.
    1. Welk van deze punten beweegt niet met een constante snelheid? Bereken van dit punt de beginsnelheid.
    2. Welke hoek maken hun banen op `t = 0` met elkaar?
    3. Botsen de punten op elkaar? Zo ja, na hoeveel seconden is dat?
    4. Met welke snelheden botsen de punten op elkaar?
    5. Hoe ver ligt het punt waarop `P` en `Q` op elkaar botsen van de oorsprong af?
    6. Hoeveel bedraagt de grootste afstand tussen beide punten?