
Parabolen
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Krommen en oppervlakken > Parabolen > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Krommen en oppervlakken > Parabolen > Inleiding
Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.
Denk aan het kiezen van een assenstelsel!
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Krommen en oppervlakken > Parabolen > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Krommen en oppervlakken > Parabolen > Uitleg
Lees eerst de Uitleg goed door.
-
Bekijk de Uitleg, pagina 1. De vergelijking van een parabool wordt afgeleid door een geschikt assenstelsel te kiezen.
- Laat zelf zien dat de vergelijking van de parabool is te schrijven als `y^2 = 4x`.
- Je kunt het assenstelsel ook zo kiezen, dat de richtlijn samenvalt met de `y`-as en het brandpunt `F(2,0)` is.
Hoe ziet in dat geval de vergelijking van de parabool er uit?
- Maak een parametervoorstelling voor deze parabool.
- Laat zien dat de vergelijking van een parabool met richtlijn `x = -0,5p` en brandpunt `F(0,5p;0)` is te schrijven als `y^2 = 2px`.
-
Teken zelf een parabool (met GeoGebra?) waarvan de richtlijn de lijn `y = 0,5p` en het brandpunt `F(0;-0,5p)` is.
Toon aan dat de vergelijking van deze parabool is te schrijven als `x^2 = -2py`.
-
Bekijk de Uitleg, pagina 2. Het gaat nu om het opstellen van de vergelijking van een raaklijn aan een parabool in een punt op de parabool.
- Waarom is het bepalen van de hellingwaarde van zo'n raaklijn bij een parabool moeilijker dan bij een cirkel?
- Ga na dat de parametervoorstelling bij deze parabool klopt.
- Je ziet hoe je de helling van de raaklijn kunt berekenen. Waarom geldt `Delta t rarr 0` als `Delta x rarr 0`?
- Bereken nu met behulp van differentiëren de richtingscoëfficiënt van de gevraagde raaklijn en stel een vergelijking van die raaklijn op.
- Laat zien dat `Q(8,8)` een punt van de parabool is en stel de vergelijking op van de raaklijn in dat punt aan de parabool.
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Krommen en oppervlakken > Parabolen > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Krommen en oppervlakken > Parabolen > Theorie
Bestudeer eerst de Theorie. In de opgaven word je naar de Voorbeelden verwezen.
Opgaven
-
In de Theorie, pagina 1 wordt verteld dat `y^2 = 2px` de vergelijking van een parabool met richtlijn `x = -0,5p` en brandpunt `F(0,5p;0)` is.
- Je verschuift de top `(0,0)` van deze parabool naar `(a,0)`. Hoe ziet de vergelijking er dan uit?
- Je verschuift de top `(0,0)` van deze parabool naar `(0,b)`. Hoe ziet de vergelijking er dan uit?
- Schrijf een vergelijking op van de parabool met brandpunt `F(4,6)` en richtlijn `x = 3`.
- Maak bij de parabool in c ook een parametervoorstelling.
-
Stel een vergelijking en een parametervoorstelling op van de parabool `p` met richtlijn `y = 1` en brandpunt `F(2,5)`.
Bekijk eventueel eerst Voorbeeld 1.
-
In de Theorie, pagina 2 gaat het over het opstellen van de vergelijking van een raaklijn aan een parabool.
Neem nu de parabool gegeven door `y^2 = 6x + 6`.
- Bereken de punten op de parabool met `x = 5`.
- Maak een parametervoorstelling bij deze parabool.
- Bereken in beide punten die je bij a hebt gevonden de richtingscoëfficiënt van de raaklijn in dat punt.
- Stel van beide raaklijnen bedoeld in c de vergelijking op.
In de theorie staat ook dat je de raaklijn aan een parabool op een andere manier kunt berekenen, namelijk met behulp van de discriminant van een kwadratische vergelijking.
- Neem het punt `P(0,5;3)` op de parabool. Stel een vergelijking op van de lijn door `P` met richtingscoëfficiënt `a`.
- Snijd deze lijn met de parabool en bereken vervolgens `a` zo, dat beide snijpunten samenvallen.
- Welke vergelijking heeft de raaklijn in `P` aan de parabool?
-
Bekijk Voorbeeld 2.
- Schrijf door kwadraat afsplitsen de vergelijking van de parabool zo, dat je er de top uit kunt aflezen.
- Bepaal de coördinaten van het brandpunt en de vergelijking van de richtlijn van deze parabool.
- Laat zien hoe de parametervoorstelling van deze parabool kan worden gevonden.
- Stel vergelijkingen op van de raaklijnen aan parabool `p` in de punten van `p` waarvoor `x = 0`.
-
In Voorbeeld 3 worden van een parabool die is gegeven door een parametervoorstelling het brandpunt en de vergelijking van de richtlijn bepaald.
- Laat zien hoe je de vergelijking `(x - 4)^2 = y - 3` kunt vinden.
- Leg uit waarom `p = 0,5` en `b = 3`.
- Waarom ligt de top van deze parabool boven de richtlijn?
- Ga zelf na, hoe brandpunt en richtlijn nu worden gevonden.
Verwerken
-
Hieronder wordt een parabool `p` omschreven. Stel er een vergelijking en een parametervoorstelling van `p` op.
- `p` heeft brandpunt `(-4,0)` en richtlijn `x = 2`.
- `p` heeft top `(0,2)` en richtlijn `y = 0`.
- `p` heeft brandpunt `(0,2)` en top `(4,2)`.
- `p` heeft brandpunt `(3,0)`, een richtlijn evenwijdig aan de y-as en gaat door `(0,4)`.
-
De parabool `p` is gegeven door de parametervoorstelling `x = t^2 - 4` en `y = 2t + 2`.
Lijn `l` gaat door `A(0,2)` en `B(3,0)`.
- Bereken van `p` de coördinaten van het brandpunt en de vergelijking van de richtlijn.
- Bereken de exacte coördinaten van de snijpunten van `p` en `l`.
- Lijn `l` snijdt `p` in twee punten. Bereken in elk van deze punten de hoek waaronder `l` parabool `p` snijdt.
Doe de volgende opdracht alleen als je de techniek van het integreren beheerst.
- Bereken de oppervlakte van het vlakdeel ingesloten door de parabool en de lijn.
-
Gegeven zijn ten opzichte van een cartesisch assenstelsel de parabool `p: (y - 2)^2 = -x + 4` en de cirkel `c: (x - 2)^2 + (y - 2)^2 = 13`.
- Teken beide krommen (met GeoGebra?) in één figuur.
- Bereken de exacte coördinaten van de snijpunten van `p` en `c`.
- Bereken van beide krommen de coördinaten van de snijpunten met de assen.
- Bereken de hoek(en) waaronder beide krommen elkaar snijden.
-
Een lijn `l` met richtingscoëfficiënt 3 raakt de parabool `p` met vergelijking `y^2 - 8y + 6x + 10 = 0`.
Bereken de exacte coördinaten van het raakpunt.
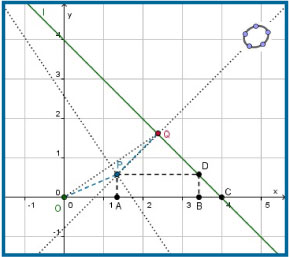 Een parabool hoeft geen symmetrieas te hebben die evenwijdig is aan de `x`-as of de `y`-as. De symmetrieas kan ook "scheef" zijn.
Neem bijvoorbeeld een parabool `p` waarvan het brandpunt de oorsprong `O` van het assenstelsel is en de richtlijn de lijn `l: x + y = 4` is.
Een parabool hoeft geen symmetrieas te hebben die evenwijdig is aan de `x`-as of de `y`-as. De symmetrieas kan ook "scheef" zijn.
Neem bijvoorbeeld een parabool `p` waarvan het brandpunt de oorsprong `O` van het assenstelsel is en de richtlijn de lijn `l: x + y = 4` is.
- Construeer deze parabool met behulp van GeoGebra.
- In de figuur hiernaast is `P` een punt van de parabool, dus `|OP| = |PQ|`.
Leid uit `|OA| = x` en `|AP| = y` af dat `|PQ|^2 = 0,5 * (4 - x - y)^2`.
- Laat zien dat voor `P` geldt: `2(x^2 + y^2) = (4 - x - y)^2`.
- Laat zien dat bij parabool `p` de vergelijking `x^2 - 2xy + y^2 + 8x + 8y - 16 = 0` hoort.
- Deze vergelijking kun je schrijven als `(x - y)^2 + 8(x + y) - 16 = 0`. Neem je nu `x - y = 4t` dan kun je ook `x + y` in `t` uitdrukken. Maak zo een parametervoorstelling van `p`.
- Bereken nu de coördinaten van de punten op `p` waarin de raaklijn evenwijdig loopt aan de `x`-as of de `y`-as.
Testen
-
Een parabool `p` is gegeven door `x = 4 - 0,1t^2` en `y = t - 3`.
- Bereken het brandpunt en de richtlijn van `p`.
- Bereken de hoek die de raaklijnen aan de parabool in de punten op `p` met `x = -6` met elkaar maken.
- In welk punt van `p` heeft de raaklijn een hellingwaarde van `-2`? Bereken de exacte coördinaten van dat punt.
-
De cirkel `c: (x - 12)^2 + (y - 2)^2 = 65` en de parabool `p: y^2 - 4y = 8x - 28` hebben vier snijpunten.
- Bereken de coördinaten van die snijpunten.
- Bereken de grootte van één van de hoeken die de cirkel en de parabool met elkaar maken.

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Krommen en oppervlakken > Parabolen > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Krommen en oppervlakken > Parabolen > Inleiding![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Krommen en oppervlakken > Parabolen > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Krommen en oppervlakken > Parabolen > Uitleg![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Krommen en oppervlakken > Parabolen > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Krommen en oppervlakken > Parabolen > Theorie Een parabool hoeft geen symmetrieas te hebben die evenwijdig is aan de `x`-as of de `y`-as. De symmetrieas kan ook "scheef" zijn.
Neem bijvoorbeeld een parabool `p` waarvan het brandpunt de oorsprong `O` van het assenstelsel is en de richtlijn de lijn `l: x + y = 4` is.
Een parabool hoeft geen symmetrieas te hebben die evenwijdig is aan de `x`-as of de `y`-as. De symmetrieas kan ook "scheef" zijn.
Neem bijvoorbeeld een parabool `p` waarvan het brandpunt de oorsprong `O` van het assenstelsel is en de richtlijn de lijn `l: x + y = 4` is.