Totaalbeeld

Samenvatten

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Vectormeetkunde > Totaalbeeld > Samenvatten

Je hebt nu het onderwerp Vectormeetkunde doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!

Begrippenlijst:

vector — kentallen — som, verschil, scalair product
inproduct van vectoren — normaalvector
plaatsvector — richtingsvector — vectorvoorstelling van een lijn
3D cartesisch assenstelsel — coördinaten en vectoren in 3D
vectorvoorstellingen en vergelijkingen van vlakken
snijdende, evenwijdige en kruisende lijnen — snijdende en evenwijdige vlakken

Activiteitenlijst:

vectoren optellen, aftrekken en scalair vermenigvuldigen — werken met kentallen
inproduct van vectoren berekenen — hoek tussen vectoren berekenen
vectorvoorstellingen van lijnen opstellen — hoeken tussen lijnen en afstanden berekenen
werken met coördinaten en kentallen in 3D
vectorvoorstellingen en vergelijkingen van vlakken in 3D opstellen
onderlinge ligging van punten, lijnen en vlakken bepalen — hoeken en afstanden berekenen

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Vectormeetkunde > Totaalbeeld > Achtergronden

Testen

Opgaven

Gegeven is de regelmatige vierzijdige piramide `T.ABCD` door `T(0, 0, 6), A(3, 3, 0), B(-3, 3, 0), C(-3, -3, 0)` en `D(3, -3,`0). Verder zijn gegeven de punten `E(-3, 9, 0)` en `F(1, -1, 4)`.
1. Teken deze piramide (of construeer hem in Cabri3D).
2. Toon aan, dat `E` op het verlengde van `CB` ligt.
3. Bereken de coördinaten van het snijpunt van lijn `EF` en vlak `TAB`.
4. Bereken de lengte van de loodrechte projectie van lijnstuk `BF` op vlak `ABCD`.
5. Vlak `V` gaat door `A` en `F` en is evenwijdig aan `BD`. `V` snijdt ribbe `BT` in punt `G`. Bereken de coördinaten van `G`.
6. Op ribbe `AD` ligt een punt `H` zo, dat de cosinus van de hoek tussen `OH` en `CT` gelijk is aan `2/sqrt(15)`. Bereken de coördinaten van `H`.

Kubus `OABC.DEFG` is in een cartesisch `Oxyz`-assenstelsel gegeven door de punten `A(6, -8, 0), C(8, 6, 0)` en `D(0, 0, 10)`. `S` is het snijpunt van `AC` en `OB`. `P` is het punt `(0, 0, 15)`.
1. Teken de kubus.
2. Bereken de coördinaten van de punten op lijn `AG` die een afstand van `sqrt(8)` hebben tot het diagonaalvlak `OBFD`.
3. `M` is het midden van `AE` en `N` dat van `CG`. Het vlak `V` gaat door `P`, `M` en `N`. Bereken de coördinaten van de snijpunten van dit vlak met de ribben van de kubus. Teken nu het deel van dit vlak dat binnen de kubus ligt.
4. Bereken de hoek die dit vlak maakt met het grondvlak `OABC` van de kubus.
5. Het vlak met vergelijking `x=p`, met `0 <= p <= 6`, snijdt de kubus volgens een rechthoek met een oppervlakte van 10. Bereken `p`.

Een driezijdige piramide `T.ABC` is gegeven door `A(0, -3, 0), B(4, -3, 0), C(0, 3, 0)` en `T(0, 0, 3)`.
1. Bewijs dat de vlakken `ABT` en `ACT` loodrecht op elkaar staan.
2. Bereken de afstand tussen de lijnen `BT` en `AC`.
3. Bereken de hoek die vlak `BCT` maakt met lijn `AB`.

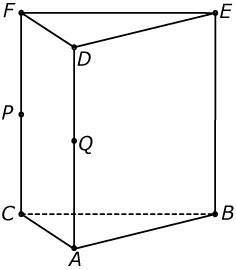In dit rechte driezijdige prisma `ABC.DEF` geldt: `AC=AB=5` en `AD=BC=6`. Punt `P` is het midden van `CF` en punt `Q` is het midden van `AD`.
1. Toon aan dat de lijnen `BF` en `DP` elkaar loodrecht kruisen.
Kies een cartesisch coördinatenstelsel `Oxyz` zo, dat `O` het midden van `BC` is, punt `A` op de `x`-as ligt en `B` en `C` op de `y`-as liggen. (De eenheden op de assen passen bij de gegeven lengtes.)
1. Bepaal de coördinaten van het punt `K` op lijn `AP` zo, dat `KF=KB`.
2. Toon aan dat driehoek `BDK` een gelijkbenige driehoek is.
3. Op diagonaal `BF` ligt een punt `L`. Door `L` gaat een rechte lijn evenwijdig aan de `y`-as. Deze lijn snijdt `CF` in punt `M`. `L` doorloopt de lijn `BF`. Bereken de maximale inhoud van piramide `L.AQMC`.

Een afgeknotte balk `ABCD.EFG` is in een cartesisch `Oxyz`-assenstelsel gegeven door `A(6, 0, 0), B(0, 0, -6), C(-6, 0, 0), D(0, 0, 6), E(0, 6, -6), F(-6, 6, 0)` en `G(0, 6, 6)`.
1. Teken deze afgeknotte balk.
2. Punt `M` is het midden van `AG` en punt `N` is het midden van `AE`. Bereken de hoek die de lijnen `MN` en `MF` met elkaar maken.
3. Een lijn door `C` snijdt de lijn `AF` en de lijn `GN`. Het snijpunt met `GN` is punt `P`. Bereken de lengte van `CP`.
4. Het vlak door de punten `C`, `M` en `N` snijdt ribbe `DG` in `Q` en ribbe `BE` in `R`. Bereken de coördinaten van `Q` en `R`.
5. Bereken de oppervlakte van vijfhoek `MNQCR`.

Toepassen

Een octaëder is een regelmatig achtvlak. Alle ribben van zo’n achtvlak zijn even lang. De figuur bestaat uit acht gelijkzijdige driehoeken.
1. Bereken de hoek tussen twee grensvlakken die een ribbe van het achtvlak gemeenschappelijk hebben.
2. Onderzoek welke mogelijke hoeken de ribben van de octaëder met elkaar kunnen maken.

Gegeven is de piramide `T.OABC` met `A(6, 0, 0), B(6, 6, 0), C(0, 6, 0)` en `T(3, 3, 12)`. Verder zijn gegeven de punten `P(2, 2, 8), Q(5, 1, 4)` en `R(112, 412, 6)`.
1. Laat zien dat de punten `P`, `Q` en `R` op ribben van de piramide liggen.
2. Teken de piramide en deze drie punten.
3. Vlak `PQR` snijdt ook het grondvlak `OABC` van de piramide. Leg uit hoe je met behulp van de drie vlakken stelling de snijlijn van `PQR` en `OABC` kunt tekenen.
4. Je kunt deze snijlijn ook berekenen. Gebruik de vergelijkingen van de vlakken `PQR` en `OABC` om een vectorvoorstelling van de snijlijn van beide te vinden. Ga na, dat je dezelfde lijn krijgt als bij c).
5. Teken nu de complete doorsnede van vlak `PQR` met de piramide (dus alle snijlijnen met de grensvlakken).

Een normaalvector van een vlak kun je berekenen door gebruik te maken van het uitwendig product van beide richtingsvectoren. Bekijk eerst wat wordt verstaan onder het uitproduct van twee vectoren via
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Vectormeetkunde > Totaalbeeld > Toepassingen
1. Laat met behulp van het inproduct zien, dat het uitproduct `vec(a) x vec(b)` van twee vectoren `veca` en `vecb` een vector is die inderdaad loodrecht op zowel `veca` als `vecb` staat.
2. Vlak `V` gaat door de punten `P(3, 4, 8), Q(6, 1, 5)` en `R(1, 5, 4)`. Stel met behulp van het uitproduct een vergelijking van dit vlak op.

Misschien ken je Polydron wel, bouwmateriaal voor ruimtelijke figuren bestaande uit aan elkaar te klikken vierkanten, driehoeken, vijfhoeken, etc. Hier zie je een vierkant en een gelijkzijdige driehoek van Polydron. Met 4 van deze vierkanten en 10 van deze gelijkzijdige driehoeken maak je de figuur hieronder. Hij is in een assenstelsel geplaatst waardoor de hoekpunten van grondvlak `ABCD` (dat uit twee vierkanten bestaat) de coördinaten `A(3, -6, 0), B(3, 6, 0), C(-3, 6, 0)` en `D(-3, -6, 0)` hebben.
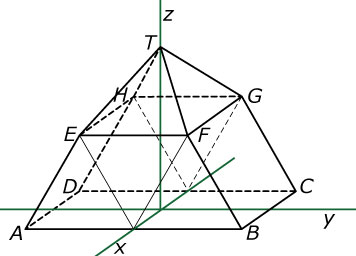
1. Bepaal nu zelf de coördinaten van de hoekpunten `E`, `F`, `G`, `H` en `T`.
2. Toon aan dat vierkant `BCGF` en driehoek `FGT` niet in één vlak liggen en bereken de hoek die ze met elkaar maken.
3. Onderzoek of de lijnen `BF` en `GT` elkaar snijden. Snijden ze elkaar niet, bereken dan hun kortste onderlinge afstand.
4. Bereken de hoek die de lijnen `CE` en `ET` met elkaar maken.
5. Het vlak door `E`, `C` en `T` snijdt nog meer ribben van de figuur. Welke ribben?

Examenopgaven

Ten opzichte van een cartesisch assenstelsel `Oxyz` zijn gegeven de punten `A(12, 0, 0), C(0, 12, 0)` en `T(12, 12, 0)`. Deze punten zijn hoekpunten van een regelmatige vierzijdige piramide `T.ABCD` met `T` als top.
1. Teken in een ruimtelijke figuur de doorsnede van de piramide en het vlak met vergelijking `y=8`. Geef een duidelijke toelichting, bijvoorbeeld door berekening van de snijpunten van dit vlak met alle ribben van de piramide.
2. Bereken de oppervlakte van deze doorsnede.
3. De lijn `AE` snijdt het vlak met vergelijking `y=8` in het punt `S`. Bereken de coördinaten van `S`.
4. Op de ribbe `BT` ligt een punt `F` zo, dat de som van de lengten van de lijnstukken `AF` en `FE` minimaal is. Bereken `AF+FE`.
(bron: examen wiskunde B havo 1985, eerste tijdvak)