Vectoren in 2D

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Vectormeetkunde > Vectoren in 2D > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Vectormeetkunde > Vectoren in 2D > Uitleg

Lees eerst de Uitleg goed door.

  1. Bekijk de Uitleg, pagina 1. De vector in de applet heeft een lengte van 1 en een richtingshoek van `alpha=30`°.
    1. Bereken zelf de `x`-component en de `y`-component van deze vector.
    2. Hoe groot zijn de componenten van een vector met lengte 10 en een richtingshoek van 30°?
    3. Geef de vector in de applet een richtingshoek van 110°. Je kunt de beide componenten aflezen uit de figuur. Controleer deze getallen door een berekening.
    4. Hoe groot zijn de componenten van een vector met een richtingshoek van 110° en een lengte van 10?
    5. Oefen het berekenen van componenten van vectoren. Neem niet alleen vectoren met lengte 1, hoewel je alleen die in de applet kunt instellen.

  2. Bekijk de Uitleg, pagina 2. Van een vliegtuig zijn de snelheden op bepaalde momenten gegeven. Je wilt de verplaatsingen berekenen.
    1. Stel in de applet de juiste verplaatsingen in. Leg uit waar de getallen `1/3` en `5/6` vandaan komen.
    2. Bereken de componenten van `1/3 * vec(v_1)` en van `5/6 * vec(v_2)`.
    3. Leid uit de antwoorden bij b) de componenten van de totale verplaatsing `vecr` af.
    4. Welke lengte en welke richtingshoek heeft `vecr`?
    5. Bereken hoeveel km hetzelfde vliegtuig zich naar het Oosten en het Noorden heeft verplaatst als het eerst 30 minuten met `240` km/h onder 60° t.o.v. het Oosten en vervolgens 40 minuten met een snelheid van `210` km/h en een koershoek van 330° t.o.v. het Oosten vliegt.

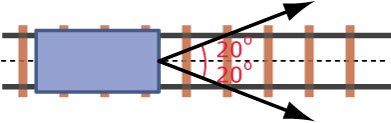  3. Een lorrie is een karretje dat op rails loopt. Twee personen trekken de lorrie met dezelfde kracht van 8 N elk aan een touw, zie figuur.
    1. Met welke kracht trekken beide personen samen aan het karretje in de richting van de rails? Maak zowel een tekening als een berekening.
    2. Beantwoord dezelfde vraag als de éne persoon trekt met een kracht van 8 N en de andere met een kracht van 6 N. De hoeken blijven gelijk.

  4. Zowel in opgave 2 als in opgave 3 heb je vectoren opgeteld. In het éne geval heb je daartoe de vectoren "staart aan kop" gelegd, in het andere geval heb je een parallellogramconstructie gebruikt. Welke van beide methodes heb je bij welke opgave gebruikt en waarom?

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Vectormeetkunde > Vectoren in 2D > Theorie

Bestudeer eerst de Theorie. In de opgaven word je naar de Voorbeelden verwezen.

Opgaven

  1. In Voorbeeld 1 ga je na, dat twee vectoren waarvan begin- en eindpunt gegeven zijn, even lang zijn.
    1. Loop zelf de berekeningen nauwkeurig na.
    2. Gegeven zijn in een cartesisch assenstelsel de punten `A(–2, 1), B(1, 6), C(28, 12)` en `D(31, 17)`. Bereken `|AB|` en `|CD|` en de richtingshoeken van `vec(AB)` en `vec(CD)`. Laat daarmee zien dat beide vectoren gelijk zijn.

  2. In Voorbeeld 2 bereken je de kentallen van een vector waarvan lengte en richting bekend zijn. Bereken de kentallen van de volgende vectoren: Geef waar mogelijk exacte uitkomsten, anders benaderingen in twee decimalen nauwkeurig.
    1. `|vecv| = 3` en `alpha= 135`°
    2. `|vecv| = 5` en `alpha = 210`°
    3. `|vecv| = 4` en `alpha = 320`°
    4. `|vecv| = 2` en `alpha = 270`°
    5. `|vecv| = 3` en `alpha = 115`°
    6. `|vecv| = 1` en `alpha = 193`°

  3. Gegeven is telkens een vector `vecv` door zijn kengetallen. Bereken de lengte en de richtingshoek van deze vector.
    1. `vecv = ((-2),(4))`
    2. `vecv = ((-20),(-40))`
    3. `vecv = ((0),(-15))`
    4. `vecv = ((sqrt(15)),(-1))`

  4. In Voorbeeld 3 zie je hoe je vectoren kunt optellen en aftrekken en vermenigvuldigen met een getal door de “staart aan kop” methode te gebruiken.
    1. Maak met de applet de vector `veca + vecb` en bepaal de bijbehorende kentallen.
    2. Maak de vector `2 veca` en bepaal de kentallen ervan.
    3. Maak de vector `2 veca + 1,5 vecb` en bepaal de kentallen ervan.
    4. Maak de vector `-2 vecb` en bepaal zijn kentallen.
    5. Ook voor vectoren geldt: `veca - vecb = veca + (-vecb)`. Gebruik dit om de verschilvector van `veca` en `vecb` te tekenen en zijn kentallen te bepalen.

  5. In Voorbeeld 4 zie je hoe het optellen, aftrekken en vermenigvuldigen met een getal van vectoren gebeurt met een parallellogramconstructie. Oefen ook hiermee; gebruik eventueel de vectoren uit opgave 8.

Verwerken

  1. Gegeven zijn de vectoren:
    `veca = ((12),(5)), vecb = ((-15),(17)), vecc = ((-6),(8)), vecd = ((0),(-5)), vece = ((13),(0))` en `vec(f) = ((13),(-25))`
    1. Bereken van elk van deze vectoren de lengte en de richtingshoek.
    2. Bepaal de kentallen van de vectoren
      • `vec(v_1) = veca + vecb`
      • `vec(v_2) = veca + 0,5vecc`
      • `vec(v_3) = vec(f) - vece - 3vecd`
      • `vec(v_4) = vecd + vece - veca`

  2. Een rondvlucht van een vliegtuig wordt bepaald door vier koersvectoren. De piloot vliegt eerst 60 km met een koers van 30°, vervolgens 100 km met een koers van 125° en daarna 50 km met een koers van 190°. Alle koersen zijn hoeken die met de klok mee zijn gemeten t.o.v. het Noorden.
    1. Maak een tekening op schaal 1 : 1.000.000 van deze rondvlucht.
    2. Kies een geschikt assenstelsel en zet elk van de beschreven koersvectoren om in een vector met kentallen. Werk in gehele km nauwkeurig.
    3. Bereken de kentallen van de vierde koersvector (die het vliegtuig terug brengt naar het vliegveld vanwaar het is vertrokken).
    4. Bereken met behulp van de kentallen hoe ver het vliegtuig na de derde koersvector van het vliegveld af is.

  3. Lijnstuk `AB` is gegeven door de punten `A(1, 2)` en `B(7, 4)` in een cartesisch assenstelsel `Oxy`.
    1. Bepaal de kentallen van vector `vec(AB)`.
    2. Vectoren die vanuit de oorsprong `O` de plaats van een punt bepalen noem je plaatsvectoren. Wat zijn de plaatsvectoren van de punten `A` en `B`?
    3. Hoe kun je vector `vec(AB)` berekenen uit de plaatsvectoren van de punten `A` en `B`?
    4. `M` is het midden van lijnstuk `AB`. Bepaal de kentallen van de plaatsvector `vec(OM)`.
    5. Als in het algemeen `A(a_1, a_2)` en `B(b_1, b_2)` zijn gegeven, wat is dan de plaatsvector van het midden `M` van `AB`?

  4. Op een hellend vlak ligt een houten blokje met een massa van `m = 0,5` kg. Wanneer de hellingshoek `a` van het vlak 20° is, staat het blokje op het punt om naar beneden te glijden. De krachten die op het blokje werken zie je in de tekening. De zwaartekracht heeft een grootte van: `F_z = m*g`. Hierin is `g ~~ 9,81` m/s2 de zwaartekrachtversnelling. De grootte van een kracht is in N (newton). Hoe groot is de wrijvingskracht?

Testen

  1. Gegeven zijn de vectoren `veca = ((-4),(2))` en `vecb = ((2),(5))`.
    1. Bereken de lengte van beide vectoren in twee decimalen nauwkeurig.
    2. Bereken de richtingshoek van beide vectoren in graden nauwkeurig.
    3. Bereken de kentallen van de vectoren `veca + vecb` en `0,5 veca - vecb`.
    4. Bereken de kentallen van de vector `vecc` zo, dat `veca + vecb + vecc = ((0),(0)).

  2. Een piloot vertrekt met zijn sportvliegtuig van vliegveld `T` en vliegt 3 uur met een constante snelheid van 140 km/h een koers 30° ten opzichte van het Noorden (met de klok mee gemeten). Daarna verandert hij zijn koers in 170° en de snelheid in 120 km/h. Na 1,5 uur moet hij een noodlanding maken.
    Over de radio geeft hij aan de verkeersleiding van vliegveld `T` door waar hij is geland en dat hij ernstig gewond is geraakt. Onmiddellijk wordt een helikopter gestuurd. Bereken hoeveel km noordelijk en hoeveel km oostelijk van `T` de noodlanding heeft plaatsgevonden.