Totaalbeeld

Samenvatten

Je hebt nu het onderwerp "Hypothesen toetsen en regressie" doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Bekijk bovendien de tekentoets die je bij de toepassingen aantreft, ook dat is bedoeld voor het eindexamen. Maak een eigen samenvatting!

Begrippenlijst:

61: begrip hypothese toetsen — nulhypothese — alternatieve hypothese — fout van de eerste soort — kritieke gebied
62: binomiale toets — significantieniveau — éénzijdig en tweezijdig toetsen
63: normale toetsing van het gemiddelde
64: tekentoets — Χ2-toets — normale toets van het verschil
65: spreidingsdiagram, puntenwolk — correlatiecoëfficiënt — lineair statistisch verband
66: lineaire regressie — regressielijn

Activiteitenlijst:

61: bij hypothese toetsen de kans op een fout van de eerst soort bepalen
62: een binomiale toets uitvoeren bij gegeven significantieniveau
63: een normale toets van het gemiddelde uitvoeren bij gegeven significantieniveau
64: enkele bijzondere toetsen uitvoeren
65: onderzoeken of tussen twee statistische variabelen een lineair verband zou kunnen bestaan met behulp van de correlatiecoëfficiënt
66: de regressielijn opstellen bij een linear verband tussen twee statistische variabelen en het regressie-effect interpreteren.

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-d > Statistiek en kansrekening > Hypothesen toetsen en regressie > Totaalbeeld > Achtergronden

Testen

  1. Een fabrikant beweert dat hoogstens 20% van de door hem geleverde producten niet deugt. Omdat de fabrikant toegeeft dat het percentage wel eens 20% zou kunnen zijn is de nulhypothese `text(H)_0: p = 0,2`.
    Om dit te toetsen kun je bijvoorbeeld een steekproef van 40 producten nemen.
    1. Hoe luidt de alternatieve hypothese?
    2. Wat stelt `p` voor?
    Als significantieniveau wordt 5% genomen.
    1. Wat wil dat zeggen?
    2. Bij welke aantallen wordt de nulhypothese verworpen?

  2. De belastingdienst beweert dat wel 30% van de Nederlanders op enigerlei wijze de belasting ontduikt. Deze mening wil je toetsen met een significantieniveau van 5%.
    1. Bepaal het kritieke gebied in een steekproef van 400 Nederlanders.
    2. Je neemt een steekproef van 20 000 Nederlanders die belasting betalen. Bepaal ook nu het kritieke gebied.

  3. In een tijdschrift stond: "In 2009 behaalde, landelijk gezien, 75% van de kandidaten op het vwo die examen deden in het vak wiskunde A een voldoende." Een zekere vwo-school had dat jaar 66 eindexamenkandidaten waarvan er 44 examen deden in wiskunde A. Slechts 7 kandidaten behaalden een onvoldoende.
    Bepaal de grootst mogelijke betrouwbaarheid waarmee je nog juist aan de uitspraak gedaan in het tijdschrift mag twijfelen.

    4. 11,911,111,412,6
    11,611,411,711,8
    11,811,812,412,5
    11,712,311,312,2
    11,912,611,711,8
  4. Op het etiket van een pot jam staat dat het percentage rietsuiker 12,4% is. Om dit te controleren wordt het percentage rietsuiker van 20 willekeurige potten jam bepaald.
    1. Formuleer de hypothesen in deze situatie. Je mag aannemen dat het percentage rietsuiker normaal verdeeld is.
    2. Schat met deze resultaten de standaardafwijking in het percentage rietsuiker.
    Deze waarde mag je bij de rest van deze opgave blijven gebruiken.
    1. Toets je hypothese met een significantieniveau `alpha = 0,10`.
    2. Bij welk gemiddeld percentage zou de nulhypothese verworpen worden?

  5. Een geldstuk is zuiver als de kans op munt gelijk is aan de kans op kruis. Of dat zo is kun je onderzoeken door maar vaak genoeg met dit geldstuk te gooien.
    1. Is er met een significantie van 1% reden om aan te nemen dat het geldstuk niet zuiver is als 47 van de 100 keer kruis gegooid wordt?
    2. Stel je voor dat er 1000 keer wordt gegooid. Bij welk aantal keren kruis is er nu reden om aan te nemen dat het geldstuk niet zuiver is? Neem weer `alpha = 0,01`.


    6. dag    		aantal
    geboorten
    04/08448
    05/08466
    06/08377
    07/08344
    08/08448
    09/08438
    10/08455
    11/08468
    12/08462
    13/08405
    14/08377
    15/08451
    16/08497
    17/08458
    18/08429
    19/08434
    20/08410
    21/08351
    22/08467
    23/08508

  6. The Great Blackout

    Op 9 november 1965 viel de stroom uit in New York City, een storing die 24 uur duurde: "The Great Blackout". Negen maanden later schreven de kranten over een geboortenexplosie in New York. De tabel vermeldt het aantal geboorten in New York in een periode van 270 tot 290 dagen na "The Great Blackout", in augustus 1966.
    Het gemiddelde aantal geboorten per dag, dat over deze periode ongeveer 435 bedraagt, blijkt echter niet zoveel hoger te liggen dan het gemiddelde over het jaar 1966 dat 430 bedraagt. Neem aan dat het aantal geboorten per dag in New York City over het gehele jaar 1966 redelijk constant is.
    1. Laat zien, dat het aantal dagen in de periode van 4 tot en met 23 augustus waarop het gemiddelde boven het jaargemiddelde ligt niet significant hoog is. Neem een significantieniveau van 5%.
    In de 20 dagen voorafgaande aan 4 augustus 1966 bleek op zoveel dagen het aantal geboorten kleiner te zijn dan 430, dat men van een significante afwijking kan spreken bij een significantieniveau van 5%.
    1. Op hoeveel dagen was er sprake van een aantal geboorten beneden het gemiddelde?
    4 augustus 1966 was een donderdag. Op de drie zondagen in de periode van 4 – 23 augustus 1966 was het aantal geboorten kleiner dan 379. Neem aan dat het aantal geboorten in New York normaal is verdeeld met een gemiddelde van 430 en een standaardafwijking van 40 in de 50 weken die volgen op de periode van 4 – 23 augustus 1966.
    1. Toon aan, dat in twee decimalen nauwkeurig de kans dat op een willekeurig gekozen dag het aantal geboorten kleiner dan 379 is, gelijk is aan 0,10.
    In de 50 zondagen die volgen op de periode van 4 – 23 augustus 1966 blijken er 10 zondagen te zijn met een aantal geboorten kleiner dan 379.
    1. Is het aantal zondagen met een geboorte kleiner dan 379 significant hoog? Neem `alpha = 5`%.

  7. Maatsysteem voor De Bijenkorf

    In 1947 hielden de wiskundigen Freudenthal en Sittig een statistisch onderzoek ten behoeve van een nieuw maatsysteem voor vrouwenkleding in opdracht van het warenhuis De Bijenkorf. Zij lieten daarbij een grote verscheidenheid aan lichaamsmaten opmeten van 5001 vrouwen. Zij vonden onder andere een sterke correlatie tussen de "taille" (de omtrek van het lichaam gemeten ter hoogte van de navel) en de "bovenwijdte" (de omtrek van het lichaam gemeten ter hoogte van de borst). De gevonden correlatiecoëfficiënt bedroeg ongeveer 0,9058.
    In hun rapport "De juiste maat" geven zij voor de bovenwijdte `b` een gemiddeld van 97,99 cm met een standaardafwijking van 10,12 cm en voor de taille `t` een gemiddelde van 80,45 cm met een standaardafwijking van 10,80 cm.
    1. Welke betekenis heeft deze hoge correlatie tussen `b` en `t` voor een spreidingsdiagram van deze twee variabelen?
    2. Stel de vergelijkingen op van de regressielijn van `b` op `t` met de constanten in twee decimalen nauwkeurig.
    3. Bereken met behulp van deze regressielijn de gemiddelde bovenwijdte van een vrouw met een taille van 90 cm.
    4. Waarom zal er in dit geval maar een klein regressie-effect zijn?

Examenopgaven

  1. Basketballen

    Jaarlijks controleert de materiaalcommissaris of de ballen van Flits voldoen aan de eisen die de basketbalbond stelt. Deze zijn:

    De omtrek van de bal mag niet minder bedragen dan 75 cm en niet meer dan 78 cm. Het gewicht mag niet minder zijn dan 600 g en niet meer dan 650 g.

    Bij zo’n controle komt hij tot de ontdekking dat het gewicht van de ballen klopt, maar dat de omtrek van 15 ballen niet in orde is. Omdat hierbij ook een redelijk aantal nieuwe ballen is, stelt hij zich in verbinding met de leverancier: het bedrijf Balfa. Dit bedrijf beweert dat het dagelijk 125 ballen produceert, waarvan de omtrek normaal verdeeld is met een gemiddelde van 76,5 cm en een standaarddeviatie van 0,70 cm. Neem aan dat deze gegevens juist zijn.
    1. Toon aan dat men kan verwachten dat 4 ballen in de dagproductie niet voldoen aan de eisen die de bond stelt aan de omtrek.
    2. Bereken in procenten nauwkeurig de kans dat in een aselecte steekproef van 5 door Balfa gemaakte ballen, elke bal voldoet aan de eisen die de bond stelt aan de omtrek.
    Op grond van de eigen gegevens beweert de verkoper van Balfa dat gemiddeld hoogstens één op de twintig ballen niet aan alle eisen van de bond voldoet. De materiaalcommissaris heeft zo zijn twijfels. Zij spreken met elkaar af de bewering van de verkoper te toetsen door middel van een aselecte steekproef van 15 stuks bij een significantieniveau van 5%. Indien het resultaat de verkoper in het ongelijk stelt, krijgt Flits de 15 nieuwe ballen uit de steekproef gratis. `X` is het aantal ballen in de steekproef dat niet voldoet aan de eisen van de bond.
    1. Bereken de kleinste waarde van `X` waarbij Flits de ballen gratis krijgt.

    (bron: examen wiskunde A vwo 1990, tweede tijdvak)


  2. Kwaliteitscontrole

    In een fabriek worden plastic zakken gevuld met suiker. De vulmachine staat afgesteld op 510 gram. Neem aan dat het gewicht van de zakken suiker normaal verdeeld is met een gemiddelde µ van 510 gram en een standaardafwijking s van 4 gram.
    1. Bereken hoeveel procent van alle zakken een gewicht minder dan 500 gram zal hebben.
    Om de kwaliteit van het vulproces te bewaken, wordt elk uur een aselecte steekproef van 5 zakken suiker genomen. Van elke zak noteert men het gewicht. Ook wordt van de steekproef het totale gewicht T berekend.
    1. Bereken de kans dat het totale gewicht van de steekproef minder is dan 2525 gram.
    Verder bepaalt men van elke steekproef het gemiddelde gewicht `bar(x)` en de spreidingsbreedte `R` (dat is het verschil tussen de grootste en de kleinste meting). Men noteert al deze gegevens op een controlekaart, de `bar(x)//R`-kaart. Op de `bar(x)//R`-kaart hieronder staan de meetresultaten van 10 steekproeven. Iedere steekproef bestaat uit 5 zakken. Op de controlekaart worden de afwijkingen van 500 gram bij ieder van deze 5 zakken genoteerd als `x_1`, `x_2`, `x_3`, `x_4` en `x_5`. Zo heeft de derde zak van de tweede steekproef een gewicht van 509 gram. Dit is genoteerd als 9.
    Het gemiddelde van de eerste steekproef is 509,6 gram. Dit wordt dan genoteerd als 9,6. De spreidingsbreedte van de eerste steekproef is `515 – 504 = 11` gram.



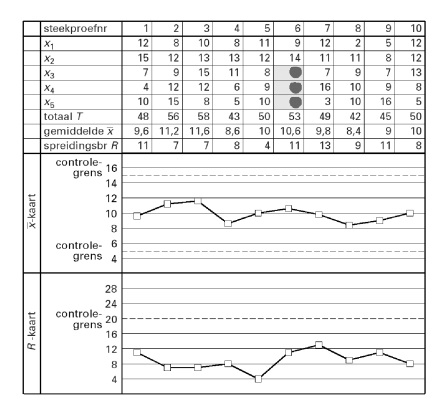
    Bij steekproef nummer 6 zijn enkele gegevens onleesbaar geworden.
    1. Welke getallen kunnen hier bijvoorbeeld gestaan hebben? Licht je antwoord toe.
    Bij de controle van het vulproces met behulp van de `bar(x)//R`-kaart let men erop of `bar(x)` of `R` de zogeheten controlegrenzen overschrijden. Deze controlegrenzen zijn in de grafieken met stippellijnen aangegeven. Zodra bij een steekproef een van deze grenzen overschreden wordt, slaat men alarm.
    Op een gegeven moment slaat men alarm bij een steekproef, terwijl met de waarde van `bar(x)` niets mis is.
    1. Wat zouden de vijf gewichten in deze steekproef bijvoorbeeld kunnen zijn? Licht je antwoord toe.
    De zakken zijn bedrukt met het bedrijfslogo. Soms is dit logo onscherp afgedrukt. Volgens de afdeling Verpakkingen heeft 5% van de zakken een onscherp logo. Een werknemer van die afdeling vermoedt echter dat dit percentage hoger is dan 5%. Er wordt een steekproef getrokken van 50 zakken. Op 6 van de 50 zakken is het bedrijfslogo onscherp.
    1. Onderzoek of de 6 zakken met het onscherpe bedrijfslogo voldoende aanleiding zijn om de werknemer in het gelijk te stellen. Neem als significantieniveau `alpha = 0,025`.

    (bron: examen wiskunde A vwo 2001, eerste tijdvak, opgave 3)

  3. Vakkenkeuze

    In het voorjaar van 1994 zijn bij een onderzoek naar vakkenkeuze 344 jongens en 493 meisjes ondervraagd die toen eindexamen havo deden. Nederlands was voor iedereen verplicht. Havo-leerlingen moesten naast Nederlands nog ten minste 5 andere vakken kiezen. In deze tabel is te zien door hoeveel procent van de ondervraagden de andere vakken zijn gekozen.

    Vakkenkeuze van jongens en meisjes op havo
    vakjongens (in %)meisjes (in %)
    Duits31,146,7
    Engels98,897,6
    Frans10,238,5
    Aardrijkskunde19,228,2
    Geschiedenis25,330,2
    Economie60,247,9
    Handelswetenschappen43,029,8
    Wiskunde A43,362,3
    Wiskunde B54,722,3
    Biologie23,545,2
    Natuurkunde57,617,0
    Scheikunde42,224,5
    Tekenen  7,015,2
    Maatschappijleer  2,9  4,5
    Muziek  0,9  3,4
    Handenarbeid  2,3  4,9
    Textiele werkvormen  0,0  0,4
    Spaans  0,0  0,6

    1. Toon aan dat van de ondervraagde leerlingen meer meisjes dan jongens economie deden.
    De meeste leerlingen hadden naast Nederlands 5 vakken gekozen. Sommige leerlingen hadden naast Nederlands 6 vakken gekozen. Geen van de leerlingen had naast Nederlands meer dan 6 vakken gekozen.
    1. Bereken hoeveel procent van de ondervraagde meisjes een extra vak deed.
    Bij het onderzoek werd ook gevraagd of je, als je opnieuw zou mogen kiezen, weer precies hetzelfde vakkenpakket gekozen zou hebben. De onderzoekers vermoedden dat ten minste de helft van de kandidaten ontevreden was over hun huidige pakket. Een onderwijsdeskundige was het daar niet mee eens. Kort voor het onderzoek beweerde hij dat minder dan de helft van alle havo-eindexamenkandidaten achteraf liever een ander pakket gekozen zou hebben.
    Neem aan dat de groep van 837 ondervraagde leerlingen een aselecte steekproef vormt uit alle havo-eindexamenkandidaten. Van deze groep zouden 359 leerlingen een ander pakket gekozen hebben, zo bleek uit het onderzoek.
    1. Onderzoek of bij een significantieniveau van 1% het onderzoeksresultaat voldoende aanleiding geeft om de onderwijsdeskundige gelijk te geven.

    (bron: examen wiskunde A vwo 2001, tweede tijdvak, opgave 1, gedeelte)


  4. Stoppen met roken

    Veel mensen beginnen op jonge leeftijd met roken en proberen daar op latere leeftijd weer mee op te houden. Dat lukt niet altijd. Het Centraal Bureau voor de Statistiek (CBS) publiceert regelmatig cijfers waarmee het rookgedrag van Nederlanders kan worden bestudeerd. In de tabel vind je enkele getallen.

    rokers en aantallen sigaretten
    jaar20012005
    aantal Nederlanders, in miljoenen16,016,3
    percentage rokers33,3%29,5%
    gemiddeld aantal sigaretten per roker per jaar45264271

    1. Bereken met hoeveel procent het totale aantal gerookte sigaretten in 2005 is afgenomen ten opzichte van 2001.
    Er zijn veel hulpmiddelen om minder te gaan roken of er zelfs helemaal mee te stoppen. Eén daarvan is het gebruik van tabletten van het merk Fumostop. Om na te gaan of Fumostop een middel is dat inderdaad helpt, wordt het volgende onderzoek uitgevoerd. Uit alle zware rokers wordt aselect een groep van 18 proefpersonen gekozen. Elke proefpersoon krijgt 10 tabletten die uiterlijk niet van elkaar verschillen. De tabletten zijn verpakt in doordrukstrips met bij elk tablet een nummer. Zie figuur.



    Elke proefpersoon moet 10 dagen lang iedere dag bij het opstaan één willekeurig gekozen tablet innemen, het nummer van dat tablet noteren en bijhouden hoeveel sigaretten hij die dag rookt. Wat de proefpersonen niet weten maar de onderzoekers wel, is dat 5 van de tabletten inderdaad van het merk Fumostop zijn. De andere 5 tabletten bevatten geen enkele werkzame stof. We geven de ‘echte’ tabletten aan met F en de andere tabletten met NF. Aan de genoteerde tabletnummers kunnen de onderzoekers zien wanneer de F- en de NF-tabletten ingenomen zijn. Nico is één van de 18 proefpersonen. De mogelijkheid bestaat dat hij om de dag een F-tablet inneemt, waarmee bedoeld wordt dat hij de ene dag een F-tablet en de andere dag een NF-tablet inneemt.
    1. Bereken de kans dat hij om de dag een F-tablet inneemt.
    De proefpersonen kiezen hun tabletten iedere dag dus volledig aselect. Het kan dus gebeuren dat een proefpersoon de eerste dag een van de tabletten met nummer 1 of nummer 2 kiest.
    1. Bereken hoe groot de kans is dat 6 of meer proefpersonen op de eerste dag van het onderzoek een van de tabletten met nummer 1 of 2 kiezen.
    De onderzoekers vermoeden dat het gebruik van F-tabletten leidt tot het roken van minder sigaretten. Om dat na te gaan, wordt van elke proefpersoon bijgehouden hoeveel sigaretten hij in totaal heeft gerookt op de vijf dagen met een F-tablet en op de vijf dagen met een NF-tablet. Het resultaat vind je in de tabel hieronder.

    aantal sigaretten
    proefpersoon123456789
    bij gebruik van F-tabletten106901097210311812410389
    bij gebruik van NF-tabletten1121081329296120145129101
    proefpersoon101112131415161718
    bij gebruik van F-tabletten879214510110097112104101
    bij gebruik van NF-tabletten10412713812412113910093118

    1. Onderzoek met behulp van een tekentoets of er voldoende aanleiding is om het vermoeden van de onderzoekers te bevestigen. Neem hierbij als significantieniveau 5%.
    Van de mensen die in 2006 rookten, rookte 24,5% per dag 20 sigaretten of meer. Rokers rookten toen gemiddeld 11,4 sigaretten per dag. Tine wil onderzoeken of het aantal sigaretten per dag normaal verdeeld zou kunnen zijn. Ze bedenkt de volgende aanpak: "Als er sprake is van een normale verdeling, dan kan ik de bijbehorende standaardafwijking berekenen. Daarna kan ik nagaan of die waarde – in combinatie met dat gemiddelde 11,4 – tot een conclusie leidt."
    1. Bereken die standaardafwijking en toon daarmee aan dat het aantal sigaretten dat een roker per dag in 2006 rookte, niet normaal verdeeld kan zijn.

    (bron: examen wiskunde A vwo 2010, eerste tijdvak)