Regressie

Antwoorden bij de opgaven

    1. Gebruik STAT PLOT op je grafische rekenmachine.
    2. `(4,3; 56)`
    3. Tussen 4 en 5 in.
    4. `r_(xy) ~~ 0,9877` en `a ~~ 4,48`.
    5. `y = 4,48x + 36,72`
    6. Ongeveer 81,5.
    1. Werk de haakjes uit en maak gebruik van `b = y - a * x`. Je krijgt dan een nogal ingewikkelde uitdrukking in `a^2` en `a`.
    2. Bedenk dat



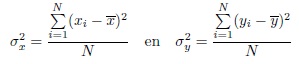
      Verder is het nogal lastig geknutsel met somtekens en zo.
    3. Als je de formule voor `r_(xy)` vermenigvuldigt met `sigma_y`, dan werk je de `sigma_y` in de noemer weg. Vervolgens weer delen door `sigma_x` en je krijgt in de noemer `sigma_x * sigma_x`, hetgeen precies staat in de formule voor `a`.
    1. Je vindt `g ~~ 0,59 * l - 44,01`.
    2. Als je van een 15-17 jarige de lengte weet, kun je met de formule voor de regressielijn het gewicht voorspellen.
    3. Ongeveer 62,5 kg.
    1. Doen, zie voorbeeld 2.
    2. Lengte `l = 174,27 + 9,30 = 183,57` geeft bij regressie van `g` op `l` een gewicht van ongeveer 64,30 kg en bij regressie van `l` op `g` een gewicht van ongeveer 67,36 kg.
    3. Bij de regressie van `g` op `l` wijkt het resultaat minder dan één s.d. af, in het andere geval meer.
  5. `a_(xy) = r_(xy) * (sigma_y)/(sigma_x)` en `a_(yx) = r_(xy) * (sigma_x)/(sigma_y)`, en dus is `a_(xy) * a_(yx) = r_(xy)^2`.
    1. `x ~~ 0,22y - 7,88`
    2. Doen.
    3. Neem bijvoorbeeld voor `x` precies één keer de standaarddeviatie boven `bar(x)`. Je zult dan voor `y` een uitkomst vinden die minder dan `sigma_y` boven `bar(y)` zit.
    1. Een positieve correlatie, dus een zoon zal over het algemeen langer zijn dan zijn vader.
    2. `z ~~ 0,47v + 95,44` en ``.
    3. Ongeveer 178,6 cm.
    4. Het regressie-effect betekent dat de voorspelling van de lengte van de zoon aan de lage kant zal zijn.
    1. Doen, zoek de bijpassende correlatiecoëfficiënt en de standaarddeviaties op.
    2. Ongeveer 0,36.
    3. De regressielijn wordt: `log(v) ~~ 0,36 log(L) + 2,67`, dus de machtsfunctie wordt: `v ~~ 10^(2,67) * L^(0,36) ~~ 468 * L^(0,36)`.
  9. Gebruik `9,65 = r_(tG) * (59,1)/(6,07)` en je vindt `r_(tG) ~~ 0,99`.
    1. Maak een tabel waarin je `t` uitzet tegen `log(N)`. Je vindt dan een bijna perfecte correlatie (`r = 0,9999...`).
    2. De bijbehorende regressielijn is: `log(N) ~~ 0,005t + 4,364`, dus is: `N ~~ 23121 * 10^(0,005t)`.
    3. Dat betekent voor 2010 ongeveer 41.116 inwoners en voor 2020 ongeveer 46.132 inwoners.
    4. Er is vrijwel geen regressie-effect omdat `r ~~ 1`.
    1. `r_(WF) ~~ -0,94`, een duidelijke negatieve correlatie.
    2. `W ~~ -0,35F + 48,30`
      De regressielijn van `W` op `F` ligt meer voor de hand omdat gezocht wordt naar een verband waarbij de werkzaamheid afhangt van de bewaartemperatuur.
    3. `W ~~ -0,63C + 37,10`
    4. Nee, want de schaalverdeling speelt geen rol bij de correlatie, het gaat alleen om de ligging van de meetpunten ten opzicht van de regressielijn.
    5. Uit de formule voor de regressielijn volgt dat de werkzaamheid in 20 dagen bij 20°C terugloopt tot ongeveer 24,5%. Voor een periode van 40 dagen loopt de werkzaamheid daarom terug tot `0,245 * 24,5 ~~ 6`%.
    1. Neem `m` voor de mouwlengte in cm en `k` voor de kniehoogte in cm.
      `sigma_m ~~ 3,04` en `sigma_k ~~ 2,70`
    2. `m ~~ 0,67k + 28,75` en `k ~~ 0,55m + 11,17`
    3. `k = 60` geeft bij regressie van `m` op `k` een mouwlengte van ongeveer 70,45 cm en bij regressie van `k` op `m` een mouwlengte van ongeveer 88,78 cm. Er is een nogal groot regressie-effect omdat `r ~~ 0,62` en dat is behoorlijk kleiner dan 1.