Correlatie

Inleiding

Naast het toetsen van hypothesen is in de mathematische statistiek het onderzoeken naar statistische verbanden een belangrijke tak van sport: wanneer bestaat er een verband tussen twee statistische variabelen? Bestaat er bijvoorbeeld een verband tussen het aantal overvliegende ooievaars en het aantal geboorten in een bepaalde streek? Of bestaat er een verband tussen lengte en gewicht bij scholieren?

Je leert nu:

Je kunt al:

Verkennen

Om te onderzoeken of er een verband bestaat tussen lengte en gewicht bij mensen van 15 tot 17 jaar oud heb je gegevens nodig. Op het werkblad LengteGewicht22h4.xls vind je de gegevens van een 4HAVO-klas van 22 leerlingen.

> Welke vier gegevens zijn er verzameld?
> Welke afspraken moet je maken bij het verzamelen van deze gegevens? Beschrijf er een paar. (Denk om de manier van meten!)
> Bekijk het getekende spreidingsdiagram. Trek je op grond van de gegevens op het werkblad de conclusie dat er zo'n verband bestaat? En is dat dan uitsluitend een statistisch verband of is het ook een oorzakelijk verband, m.a.w. wordt een groter gewicht veroorzaakt door een grotere lengte?

Uitleg

Als je vermoedt dat er tussen twee variabelen `x` en `y` een lineair verband bestaat, maak je een spreidingsdiagram dat de vorm van een puntenwolk krijgt. De mate waarin tussen de twee variabelen een lineair verband bestaat wordt gegeven door de correlatiecoëfficiënt, aangeduid door `r_(xy)`.

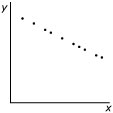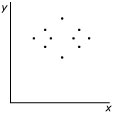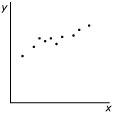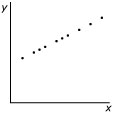`r_(xy) = -1``r_(xy) = 0``r_(xy) = 0,6``r_(xy) = 1`

De correlatie tussen `x` en `y` wordt beter naarmate `r_(xy)` dichter bij `1` of `-1` ligt. Maar hoe bereken je nu die correlatiecoëfficiënt?

Daarbij gebruik je het punt `(bar(x),bar(y))` waarin `bar(x)` het gemiddelde van de `x`-waarden en `bar(y)` het gemiddelde van de `y`-waarden is. Met behulp van die gemiddelden kan het grafiekgebied in vier delen I, II, III en IV worden verdeeld (zie figuur). Je kunt nu voor elk van de `N` punten `(x_i, y_i)` het getal `(x_i - x)(y_i - y)` berekenen. In de gebieden I en III is dit getal voor elk punt positief: deze punten dragen bij aan een positieve correlatie. In de gebieden II en IV is dit getal voor elk punt juist negatief: deze punten dragen bij aan een negatieve correlatie. Het gemiddelde van alle `N` getallen `(x_i - x)(y_i - y)` is een goede maat voor de correlatie.
Deze maat heet de covariantie van de puntenwolk: covariantie `= (Sigma_(i=1)^N (x_i - x)(y_i - y))/N`.
Deze maat voor de correlatie in een puntenwolk hangt nog af van de eenheden waarin `x` en `y` zijn gemeten. Dat kun je voorkomen door telkens `(x_i - x)` te delen door de bijbehorende standaarddeviatie `sigma_x` en ook `(y_i - y)` telkens te delen door `sigma_y`. Je krijgt dan de correlatiecoëfficiënt, die niet langer afhangt van de gekozen eenheden: `r_(xy) = (Sigma_(i=1)^N (x_i - x)(y_i - y))/(N * sigma_x * sigma_y)`.
In Excel is de berekening van de correlatiecoëfficiënt niet al te moeilijk uit te voeren. Zeker niet als je de gemiddelden en de standaarddeviaties al hebt berekend met de statistische functies. Je maakt dan een kolom voor de getallen `(x_i - x)(y_i - y)`. En daarna bereken je het gemiddelde van die kolom. Dat gemiddelde deel je nog door beide standaarddeviaties.
Overigens kent Excel ook statistische functies als COVARIANTIE en CORRELATIE.

‡

Opgaven

  1. Bekijk dit spreidingsdiagram.
    1. Is er op het oog sprake van een goede correlatie tussen `x` en `y`?
    2. Schat de correlatiecoëfficiënt.
    3. Welke soort formule hoort er bij `y` als functie van `x`?
    4. Waarom is de schaalverdeling op de assen niet van belang voor de correlatie?

  2. Op het werkblad LengteGewicht22h4.xls vind je de gegevens van een 4HAVO-klas van 22 leerlingen.
    1. Bereken ook het gemiddelde, de standaarddeviatie en de spreidingsbreedte van zowel de lengtes `l` als de gewichten `g`. Gebruik de statistische functies GEMIDDELDE en STDEVP.
    2. Is deze steekproef voldoende representatief voor 15-17 jarigen? Motiveer je antwoord.
    3. Ga met behulp van normaal waarschijnlijkheidspapier na of de lengtes van de 22 leerlingen in de voorgaande tekst ongeveer normaal verdeeld zijn. Doe dit ook voor de gewichten.
    4. Bereken de correlatiecoëfficiënt bij het verband tussen de lengte en het gewicht van de 22 leerlingen. Is er sprake van een goede correlatie tussen `l` en `g`?

Theorie

In een spreidingsdiagram van twee statistische variabelen `x` en `y` zet je alle combinaties `(x,y)` als een puntenwolk in een assenstelsel. Of er een sterk lineair statistisch verband bestaat tussen de variabelen wordt bepaald door de correlatiecoëfficiënt `r_(xy)`. Er geldt: `r_(xy) = (Sigma_(i=1)^N (x_i - x)(y_i - y))/(N * sigma_x * sigma_y)`.

`r_(xy) = -1``r_(xy) = 0``r_(xy) = 0,6``r_(xy) = 1`

De correlatie tussen `x` en `y` wordt beter naarmate `r_(xy)` dichter bij `1` of `-1` ligt.

Een verband waarbij de toename (of afname) van de éne variabele een gevolg is van een toename (of afname) van de andere heet een causaal verband: er is dan sprake van oorzaak en gevolg. Een statistisch verband tussen twee variabelen hoeft niet causaal te zijn. Andere variabelen kunnen de oorzaak zijn dat er bij twee variabelen een statistisch verband optreedt. Het is zeker niet zo, dat een grotere lengte veroorzaakt dat je daardoor automatisch ook een groter gewicht hebt.

‡

Voorbeeld 1

Op het werkblad LengteGewicht22h4.xls vind je de gegevens van een 4HAVO-klas van 22 leerlingen. Je kunt deze gegevens ook in de grafische rekenmachine invoeren en die de correlatiecoëfficiënt laten berekenen. In de figuren hieronder zie je hoe dit op de TI83/84 in zijn werk gaat. Je hebt er het rekenalgoritme LinReg voor nodig. Dat staat voor "lineaire regressie" en wordt in het volgende onderdeel nader bekeken.

      
      

‡

Opgaven

  1. Voer de berekening van de correlatiecoëfficiënt bij de gevevens van de 4HAVO-klas uit Voorbeeld 1 zelf uit met behulp van de grafische rekenmachine.

  2. De inspectie voor het onderwijs vergelijkt van een bepaalde school de cijfers voor wiskunde B van het SE (schoolexamen) en het CE (centraal examen). In de tabel vind je de gegevens van een klas van 19 leerlingen.

    leerling 1  2  3  4  5  6  7  8  9 10111213141516171819
    SE-cijfer6,06,75,87,15,46,58,86,97,95,16,16,16,47,45,96,27,16,86,3
    CE-cijfer 6,4 6,3 5,2 6,5 5,4 6,1 9,0 6,8 7,5 5,6 6,0 6,5 6,0 6,5 6,0 6,6 7,0 6,6 6,4


    Je zou kunnen onderzoeken of er een lineair statistisch verband is tussen het CE-cijfer `c` en het SE-cijfer `s`. Teken een bijpassend spreidingsdiagram en ga door berekening van de correlatiecoëfficiënt na of zo'n verband bestaat.

Verwerken

  1. In de volgende tabel zie je de examenresultaten voor de vakken Physics (natuurkunde) en Mathematics (wiskunde) van 100 studenten van een College in de Verenigde Staten:


    1. Onderzoek of de "Physics Grades" normaal zijn verdeeld. Bereken het bijbehorende gemiddelde en de standaarddeviatie.
    2. Onderzoek of de "Mathematics Grades" normaal zijn verdeeld. Bereken het bijbehorende gemiddelde en de standaarddeviatie.
    3. Waarom kunnen dit alleen geschatte gemiddelden en standaarddeviaties zijn?
    4. Kun je bij deze tabel een puntenwolk maken zoals die bij de gegevens over lengte en gewicht in de tekst? Hoe dan?
    Er wordt een verband verondersteld tussen het resultaat voor wiskunde `m` en dat voor natuurkunde `p`.
    1. Hoe bepaal je in dit geval (een schatting van) de correlatiecoëfficiënt?
    2. Bereken nu de (schatting van de) correlatiecoëfficiënt bijvoorbeeld met behulp van Excel. Geef een benadering in twee decimalen nauwkeurig.
    3. Is er een duidelijke correlatie tussen `m` en `p`?

  2. De formule voor de correlatiecoëfficiënt is te herschrijven tot:

    `r_(xy) = (bar(x * y) - bar(x) * bar(y))/(sigma_x * sigma_y)`

    Laat dat zien door in de formule in de tekst de haakjes uit te werken. (Als je de correlatiecoëfficiënt handmatig moet uitrekenen gaat dat met deze formule iets sneller.)

  3. Soms is er wel sprake van een goede correlatie tussen twee statistische variabelen, maar kun je toch je vraagtekens zetten bij het verband tussen beide.
    1. In een provincie neemt het aantal ooievaars en het aantal geboorten af. Het spreidingsdiam geeft een statistisch verband te zien. Bestaat er een causaal verband tussen aantal ooievaars en het aantal geboorten?
    2. Leg uit waarom er wel een statistisch verband is tusen ijsverkoop en verkoop van zonnebrillen in de zomer maar geen causaal verband.

  4. Om te onderzoeken of er enig verband bestaat tussen de lengte van een vader en die van zijn zoon zijn de lengtes van 12 vaders en die van hun oudste zoons gemeten op het moment dat die zoons volwassen werden. De gegevens staan in deze tabel.

    lengte vader `v` in cm173168178170180165185175180178183188
    lengte zoon `z` in cm180175180173183175180173188178180185

    1. Teken een spreidingsdiagram (een puntenwolk) bij deze gegevens.
    2. Bereken de correlatiecoëfficiënt in twee decimalen nauwkeurig.
    3. Kun je zeggen dat er een lineair verband bestaat tussen `v` en `z`?

  5. Biologen veronderstellen op grond van metingen dat er bij vliegende dieren een verband bestaat tussen de lichaamslengte `L` (in cm) en de vliegsnelheid `v` (in cm/s).

    Vliegsnelheid en lichaamslengte bij verschillende dieren


    Soort
    Lengte
    `L` in cm    		Vlieg-
    snelheid
    `v` in cm/s
    1.Drosophila melanogaster (fruitvlieg)  0,2  190
    2.Tabanus affinis (paardenvlieg)  1,3  660
    3.Archilochus colubris (kolibriesoort)  8,11120
    4.Anax sp. (waterjuffer)  8,51000
    5.Eptesicus fuscus (grote bruine vleermuis) 11,0  690
    6.Phylloscopus trochilus (fitis) 11,01200
    7.Apus apus (gierzwaluw) 17,02550
    8.Cypselurus cyanopterus (vliegende vis) 34,01560
    9.Numenius phaeopus (regenwulp) 41,02320
    10.Anas acuta (pijlstaarteend) 56,02280
    11.Olor columbianus bewicki (kleine zwaan)120,01880
    12.Pelecanus onocrotalus (witte pelikaan)160,02280

    1. Maak een spreidingsdiagram met `v` op de verticale en `L` op de horizontale as.
    2. Bereken de correlatiecoëfficiënt. Is er sprake van een duidelijke correlatie? Bestaat er tussen `v` en `L` een verband van de vorm `v = a * L + b`?
    3. Maak een tabel voor `log(L)` en `log(v)` en teken een spreidingsdiagram voor deze twee variabelen.
    4. Bereken de correlatiecoëfficiënt voor de variabelen `log(L)` en `log(v)`.
    5. Er bestaat tussen `L` en `v` dus een verband van de vorm `log(v) = a * log(L) + b`. Laat zien dat dit betekent dat `v` een machtsfunctie is van `L`.

Testen

  1. Iemand probeert aan te tonen dat de klassengrootte van invloed is op de leerprestaties. Zij vergelijkt - onder zoveel mogelijk gelijke omstandigheden - de gemiddelde cijfers voor drie wiskundetoetsen in 10 klassen met uiteenlopende leerlingenaantallen. Hier zie je de verzamelde gegevens.

    aantal leerlingen `a`gemiddelde cijfer `c`
    306,1
    256,6
    325,5
    247,2
    187,4
    196,9
    305,2
    227,1
    296,0
    147,8


    1. Maak een spreidingsdiagram met `c` op de verticale en `a` op de horizontale as. Waarom is dit een logische keuze?
    2. Bereken de correlatiecoëfficiënt. Is er sprake van een duidelijke correlatie? Bestaat er tussen `a` en `c` een lineair statistisch verband?
    3. Welke conclusie zou deze onderzoekster kunnen trekken? Geef daar commentaar op.

  2. In 1947 hielden de wiskundigen Freudenthal en Sittig een statistisch onderzoek ten behoeve van een nieuw maatsysteem voor vrouwenkleding in opdracht van het warenhuis De Bijenkorf. Zij lieten daarbij een grote verscheidenheid aan lichaamsmaten opmeten van 5001 vrouwen. In het bestand StatFS-Bijenkorf1947.xls vind je enkele gegevens. Gebruik de werkbladen "lengte-gewicht", "mouwlengte-kniehoogte" en "voetlengte-breedte".
    1. Waarom was De Bijenkorf geïnteresserd in dergelijke gegevens? En waarom zijn eventuele verbanden als die tussen voetlengte en voetbreedte van belang?
    2. Op de drie genoemde werkbladen is er sprake van een mogelijk verband tussen twee variabelen. Hoe zou je in dit geval een spreidingsdiagram tekenen?
    3. En hoe zou je een correlatiecoëfficiënt berekenen? Waarom is het hier handiger om over de oorspronkelijke ruwe meetgegevens te beschikken?