Continue stochast

Inleiding

Een bedrijf is geïnteresseerd in de tijd die nodig is om een klant te helpen, de transactietijd. Je kunt die tijd in klassen indelen (bijvoorbeeld van hele minuten) en zo bijhouden hoeveel minuten een transactie duurt. Je maakt dan een kansverdeling voor de variabele transactietijd. Maar de transactietijd kan in feite elke (positieve) reële waarde aannemen. Door steeds kleinere tijdsintervallen te nemen kun je een kansverdeling voor deze continue kansvariabele opstellen, benaderen.

Je leert nu:

het begrip continue stochast;
het begrip kansdichtheid bij een continue stochast;
door integreren kansen bij een continue stochast berekenen.

Je kunt al:

werken met discrete stochasten.

Verkennen

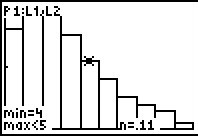
Een bedrijf heeft door tellingen een frequentieverdeling opgesteld voor de tijd die nodig is om een klant te helpen. Voor deze transactietijd (in minuten) geldt:

t (min.)	1	2	3	4	5	6	7	8	9	10
P(T = t)	0,16	0,19	0,19	0,15	0,11	0,08	0,05	0,04	0,03	0,01

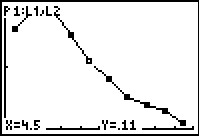
Je kunt dit opvatten als een kansverdeling voor een discrete stochast T. Maar T kan in feite elke (positieve) reële waarde aannemen. Door steeds kleinere tijdsintervallen te nemen kun je een kansverdeling voor deze continue stochast opstellen, benaderen. Het lijndiagram laat dit al een beetje zien. (Merk op dat voor de juiste figuren de klassemiddens van elke minuut moeten worden ingevoerd in de GR.)

> Hoe groot is de kans dat een klant minder dan 4 minuten transactietijd kost?
> Hoe geef je die kans in het staafdiagram weer? En in het lijndiagram?
> Hoe bepaal je de kans dat een klant minder dan 4,75 minuten transactietijd kost?

Uitleg

Bekijk de frequentieverdeling van de transactietijd T die hierboven staat.

De kans dat een klant hoogstens 4 minuten transactietijd kost is:
P(T ≤ 4) = 0,16 + 0,19 + 0,19 + 0,15 = 0,69.
Dit is de oppervlakte van de eerste vier staafjes van het staafdiagram.
Het is ook de oppervlakte onder het lijndiagram vanaf t = 0 tot t=4.

Maar T kan in feite elke (positieve) reële waarde aannemen. Door steeds kleinere tijdsintervallen te nemen kun je een kansverdeling voor deze continue stochast opstellen, benaderen.(Merk op dat voor de juiste figuren de klassemiddens van elke minuut moeten worden ingevoerd in de GR.)

De kans dat een klant hoogstens 4,75 minuten transactietijd kost kun je benaderen door de oppervlakte te schatten onder de kromme lijn die de middens van de bovenkanten van de staafjes verbindt vanaf t = 0 tot t=4,75.
Bij deze kromme hoort een kansdichtheidsfunctie f(t).

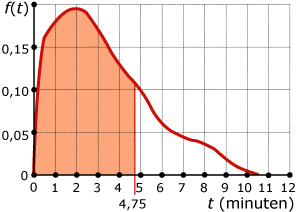
De transactietijd (de afhandelingstijd per klant) is een continue stochast T die alle positieve reële waarden kan aannemen. Door tellingen over steeds kleinere tijdsintervallen kun je een kansdichtheidsfunctie benaderen. De bijbehorende kansen worden dan weergegeven door een deel van de oppervlakte onder de kromme die bij deze functie hoort. Dergelijke kansen bereken je daarom door integreren.
Bijvoorbeeld P(T ≤ 4,75) = $\int_{0}^{4,75} f (t) d t$ .
Daarvoor moet je dan wel een functievoorschrift voor f(t) hebben. Anders moet je de oppervlakte schatten m.b.v. de tekening.

Omdat de totale kans wel 1 moet zijn (net al bij een kansverdeling de som van alle kansen 1 is), moet $\int_{0}^{\infty} f (t) d t$ = 1.
Hieraan moet elke kansdichtheidsfunctie f voldoen.
Een kansverdeling kun je bij een continue stochast niet maken.

‡

Opgaven

Bekijk de relatieve frequentieverdeling van de transactietijd in Verkennen en in de Uitleg.
1. Teken zelf op papier het bijbehorende kanshistogram. Waarom is `T` nu een discrete toevalsvariabele?
2. Bepaal de kans dat je hoogstens 3 minuten moet wachten, dus `text(P)(T <= 3)`.
3. Teken door de middels van de staven van je histogram een vloeiende kromme die goed past bij het histogram. Waarom kun je `T` eigenlijk opvatten als een continue stochast?
4. Schat in geval je `T` opvat als een continue stochast `text(P)(T <= 3)`.
5. Waarom is de kans dat je hoogstens 3 minuten moet wachten eigenlijk `text(P)(T <= 3,5)`?

Gebruik de vloeiende grafiek die je in de voorgaande opgave hebt gemaakt.
1. Arceer het gebied dat de kans voorstelt dat de transactietijd gelijk is aan 3 minuten en leg uit waarom dit gebied wordt begrensd door de lijnen `t = 2,5` en t = `3,5`. Geef een schatting van deze kans.
2. Bepaal op dezelfde manier de kans op dat de transactietijd minstens 3 minuten is.
3. Welk percentage hoort bij het hele gebied onder deze grafiek?

Bekijk in de Uitleg, pagina 2 hoe je bij een continue stochast kansen berekent door middel van integreren.
1. Wat stelt in dit verband de kansdichtheidsfunctie voor? En waarom is het belangrijk om die te weten?
2. Schrijf de kans die wordt bedoeld bij a van de voorgaande opgave als integraal.

Theorie

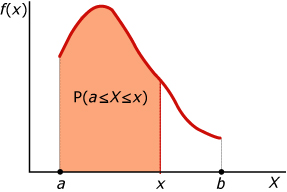
Een toevalsvariabele X die alle reële waarden uit een bepaald interval [a,b] kan aannemen noem je een continue stochast. Kun je daarbij een kansdichtheidsfunctie bepalen, dan worden de bijbehorende kansen weergegeven door een deel van de oppervlakte onder de kromme die bij deze functie hoort. Dergelijke kansen bereken je daarom door integreren.
Bijvoorbeeld P(a ≤ X ≤ x) = $\int_{a}^{x} f (x) d x$ .
Daarvoor moet je dan wel een functievoorschrift voor f(t) hebben. Anders moet je de oppervlakte schatten m.b.v. de tekening.

Omdat de totale kans 1 moet zijn, is $\int_{a}^{b} f (x) d x$ = 1.
Hieraan moet elke kansdichtheidsfunctie f voldoen.
Een kansverdeling kun je bij een continue stochast niet maken.

‡

Voorbeeld 1

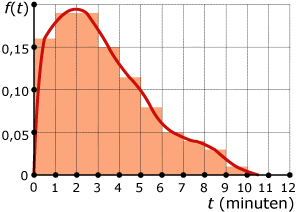
In een callcenter is de transactietijd T de tijd die nodig is om een klant te woord te staan. T is een continue stochast met kansdichtheidsfunctie f(t) = 0,25te^–0,5t.
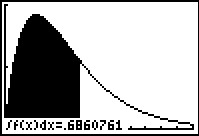
Ga na dat deze functie inderdaad als kansdichtheid kan dienen en past bij de kromme in deze figuur.
Bereken P(T ≤ 4,75) in vier decimalen nauwkeurig.

Antwoord

T is een continue stochast op $[0, \to 〉$ .
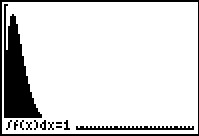
Voor f moet gelden: $\int_{0}^{\infty} f (t) d t$ = 1.

Met de GR ga je na dat dit (bij benadering) klopt.
Bekijk je vervolgens de tabel van f dan blijken de waarden bij 0, 1, 2, ..., 10 redelijk bij de figuur te passen.

Verder is: P(T ≤ 4,75) = $\int_{0}^{4,75} f (t) d t$ ≈ 0,6861.

‡

Voorbeeld 2

Een bekende continue toevalsvariabele is de stochast X met kansdichtheidsfunctie
f(x) = $\frac{1}{\sqrt{2 π}} \cdot e^{- 0,5 x^{2}}$ .
Laat met de GR zien, dat deze functie inderdaad een kansdichtheid kan zijn.
Bereken P(–1 ≤ X ≤ 1).

Antwoord

Voor f moet gelden $\int_{- \infty}^{\infty} f (x) d x$ = 1.
Door deze integraal met de GR te benaderen kun je nagaan dat dit (waarschijnlijk) klopt.

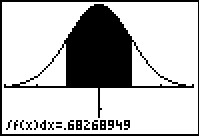
P(–1 ≤ X ≤ 1) = $\int_{- 1}^{1} f (x) d x$ ≈ 0,6827.

‡

Voorbeeld 3

Stochast X kan alle reële waarden aannemen uit het interval [0,4].
De bijpassende kansdichtheidsfunctie f heeft de vorm f(x) = –p(x – 2)².
Welke waarde heeft p?

Antwoord

Voor f moet gelden $\int_{0}^{4} f (x) d x$ = 1.
De integraal is te bepalen m.b.v. primitiveren.
Dus moet gelden: $[\frac{1}{3} p {(x - 2)}^{3}] \begin{matrix} 4 \\ 0 \end{matrix}$ = 1.

Ga na, dat dit betekent dat p = $\frac{3}{16}$ .

‡

Opgaven

In Voorbeeld 1 wordt opnieuw het berekenen van de kans op een bepaalde transactietijd bekeken.
1. Ga na dat de gegeven kansdichtheidsfunctie past bij de gemeten transactietijden.
2. Laat zien dat voor deze kansdichtheidsfunctie geldt `int_(0)^(10) f(t) text(d)t ~~ 1`.
3. Ga de schatting van `text(P)(T <= 4,75)` zelf na.
4. Hoe groot is de kans op meer dan 10 minuten transactietijd? Schrijf deze kans als integraal en benader dan die integraal met de grafische rekenmachine.
5. Bereken de kans op een transactietijd van tussen de 2 en de 3 minuten.
6. Waarom is de kans op een transactietijd van precies 4 minuten gelijk aan 0?
7. Waarom is `text(P)(T <= 4,75) = text(P)(T < 4,75)`?

Een veel voorkomende continue stochast is de normale stochast. In Voorbeeld 2 zie je daarvan de standaard kansdichtheidsfunctie. Bekijk eerst even de grafiek van deze standaard normale kansdichtheidfunctie `f(x)`.
1. Toon aan dat de grafiek van `f` symmetrisch is t.o.v. de `y`-as.
2. Bereken de coördinaten van de top van `f`.
3. Bereken de coördinaten van de buigpunten van `f`.
4. Ga ook zelf na dat `f` een geschikte kansdichtheidsfunctie is.
5. Bereken `text(P)(-2 < X < 2)`.
6. Bereken `text(P)(x >= 1,6)`.

Als de lengte van een groep personen gemiddeld 180 cm is met een standaardafwijking van 5 cm, dan past daar deze kansdichtheidsfunctie bij
`l(x) = 1/(5 * sqrt(2pi)) * text(e)^(- 1/2 * ((x - 180)/5)^2)`
1. Ga na dat deze kansdichtheidsfunctie eenzelfde grafiek heeft als die van de vorige opgave.
2. Welke verschuiving en welke vermenigvuldigingen moet je op de grafiek van `f` toepassen om die van `l` te krijgen?
3. Ga na, dat `l` een geschikte kansdichtheidsfunctie is.
4. Bepaal de coördinaten van de top en de buigpunten van `l`.
5. Bereken `text(P)(180 - 10 < X < 180 + 10)`. Vergelijk je antwoord met dat van e van de vorige opgave. Wat valt je op?
6. Bereken `text(P)(178 < X < 186)`.
7. Hoe groot is de kans dat in deze groep iemand van 2 meter of langer voorkomt?

Gegeven is de continue toevalsvariabele `X` door de kansdichtheidsfunctie `f(x) = x/a` waarbij `0 <= x <= 10`.
Functie `f` is alleen een kansdichtheidsfunctie als de oppervlakte onder de grafiek gelijk is aan 1 en als alle functiewaarden groter of gelijk aan 0 zijn. Bekijk eventueel Voorbeeld 3.
1. Bepaal de waarde van `a` waarvoor dit zo is.
2. Bereken `text(P)(0 < X < 3)`.
3. Hoeveel procent hoort er bij het gebied onder de grafiek tussen `2` en `8`?
4. Bereken `text(P)(X > 5)`.
5. Bereken `text(P)(X = 3)`.

Verwerken

Voor de afhandelingstijd `T` van telefoontjes in een call-center is een model opgesteld.
Bij het percentage P van de gesprekken met een tijdsduur kleiner of gelijk aan `T = t` minuten geldt de kansdichtheidsfunctie `f(t) = 0,042t * text(e)^(-0,20t)` met `0 <= t <= 30`.
1. Laat zien dat er inderdaad sprake is van een kansdichtheidsfunctie.
2. Schrijf de kans op een transactietijd van hoogstens 10 minuten als een integraal. Benader vervolgens deze kans met behulp van die integraal.
3. Bereken op dezelfde manier de kans op een transactietijd van minstens 10 minuten.
4. Hoeveel procent van de transacties duurt tussen de 5 en de 10 minuten?
5. Hoeveel procent van de transacties duurt precies 5 minuten?

Het geboortegewicht `G = x` kilogram van zuigelingen ligt ongeveer rond de 3,6 kg. Hieronder zie je de verdeling van de gewichten van 500 zuigelingen.

gewicht (kg) 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 4,0 4,1 4,2

aantal 3 8 22 41 73 85 93 83 53 28 9 2
1. Geef de resultaten weer in een histogram.
2. Bereken het gemiddelde `mu(G)` en de standaardafwijking `sigma(G)` van deze steekproef.
Bij deze steekproef past een kansdichtheidsfunctie van de vorm `f(x) = 1/(sigma * sqrt(2pi)) * text(e)^(- 1/2((x - mu)/sigma)^2)`.
1. Teken de grafiek van `f` op de grafische rekenmachine in het kanshistogram.
2. Schat met behulp van het histogram de kans dat een baby bij de geboorte minder dan 3,45 kg weegt.
3. Bepaal met behulp van een integraal de kans dat een baby bij de geboorte minder dan 3,45 kg weegt.

Bij de bloeddruk `X` van volwassenen tussen de 20 en de 40 jaar hoort bij benadering een kansverdeling die wordt bepaald door de kansdichtheidsfunctie `f(x) = 0,044 * text(e)^(-0,006(x - 130)^2)`. Hierin is `x` in mm kwikdruk.
Als de bloeddruk van een volwassene in die leeftijdscategorie hoger is dan 150 mm kwikdruk wordt er bij een medisch testrapport "hoge bloeddruk" aangegeven.
1. Toon aan dat `f` bij goede benadering een kansdichtheidsfunctie is.
2. Welke integraal stelt de kans voor dat iemand een bloeddruk van boven de 130 mm kwikdruk heeft? Hoe groot is die kans?
3. Hoeveel procent van de volwassenen tussen 20 en 40 jaar hebben in dit kansmodel last van "hoge bloeddruk"?

De kansverdelingsfunctie van een stochast `X` ziet er als volgt uit: `text(P)(X <= x) = 1 - text(e)^(-x)` voor `x >= 0` en `text(P)(X <= x) = 0` voor `x < 0`.
1. Teken de grafiek van deze functie en toon aan dat hij voldoet aan de eisen waaraan een kansverdeling moet voldoen.
2. Bepaal het voorschrift van de bijbehorende kansdichtheidsfunctie `f(x)`.
3. Bereken `text(P)(X < 1)`.
4. Bereken `text(P)(0 < X < 3)`.
5. Bereken `text(P)(X > 3)`.

Testen

Gegeven is de continue stochast `X` met kansdichtheidsfunctie `f(x) = a(4 - x)` met `0 <= x <= 4`.
1. Bereken `a`.
2. Bereken de kans dat `X` tussen 1 en 3 ligt.

Een bepaald type gloeilampen heeft een gemiddelde levensduur van 680 uur. Voor de levensduur `L = x` uur van dit type gloeilampen is een continu kansmodel opgesteld met een kansdichtheidsfunctie `f(x) = 0,0088 text(e)^(-0,00025(x - 680)^2)`.
1. Hoeveel procent van deze lampen heeft een levensduur tussen 635 en 725 uur?
2. Hoeveel procent van deze lampen heeft een levensduur van meer dan 770 uur?

gewicht (kg)	3,1	3,2	3,3	3,4	3,5	3,6	3,7	3,8	3,9	4,0	4,1	4,2
aantal	3	8	22	41	73	85	93	83	53	28	9	2