Gegevens samenvatten

Antwoorden bij de opgaven

1. Het modale cijfer is het cijfer dat het vaakst voorkomt. Hier zegt het niet veel, want misschien komt alleen 6,7 twee keer voor en zijn alle andere cijfers veel hoger of lager, maar wel onderling verschillend.
2. klas A: 6,2 en klas B:6,5
3. De mediaan (middelste cijfer) zegt niet veel, hoewel je dan zeker weet dat de helft van de cijfers zeker hoger of gelijk aan 6,2 of 6,5 is (en de andere helft is lager).
4. klas A: 6,0 en klas B: 6,5
5. Klas B is beter, het gemiddelde is behoorlijk hoger, en de mediaan is ook hoger.
1. A: 6,1; B: 6,1; C: 7,4; D: 6,1
2. A: 6,2; B: 6,0; C: 6,9; D: 6,0
  De cijfers van A liggen meer gespreid dan die van B.
3. Het gemiddelde van C is behoorlijk hoger, de cijfers van C liggen meer naar rechts op de getallenlijn.
4. Nee, eigenlijk niet. De cijfers van D liggen vaak toch dichter bij het gemiddelde cijfer.
5. Het gemiddelde is 0,0. Verbazend is dat niet: het gemiddelde is het evenwichtspunt van de verdeling.
6. Het gemiddelde van de kwadraten wordt 3,0.
  Om een goede spreidingsmaat te zijn zouden de cijfers van A tussen `6,1 - 3,0 = 3,1` en `6,1 + 3,0 = 9,1` moeten liggen. Aan de linkerkant klopt dat wel zo'n beetje, maar aan de rechterkant is de 9,1 veel te hoog. Dat komt door het kwadrateren.
7. Inderdaad is `sqrt(3,00) ~~ 1,73`.
8. Voor B is de standaardafwijking ongeveer `sqrt(0,62) ~~ 0,79`.
9. Voor D is de standaardafwijking ongeveer `sqrt(0,58) ~~ 0,76`. De standaardafwijking van D is iets kleiner dan die van B. Dat verwacht je ook: de cijfers van D liggen meestal dichter bij het gemiddelde dan de cijfers van B.
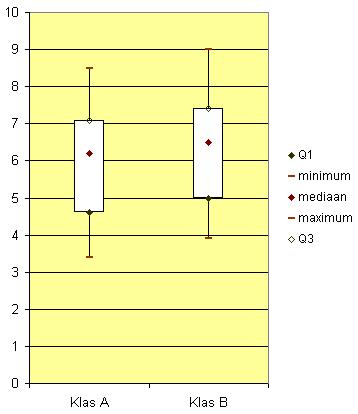
Klas A: mediaan = 6,2 en kwartielafstand = 2,5
Klas B: mediaan = 6,5 en kwartielafstand = 2,4
Voor de boxplots:
Klas A: laagste = 3,4 en hoogste = 8,5
Klas B: laagste = 3,9 en hoogste = 9,4
Modus = 65
Mediaan = 68
Gemiddelde `~~ 66,16`
Alle beweringen zijn onjuist.
Modus = 63
Mediaan = 65
Gemiddelde `~~ 65,73`
A: onjuist
B: juist
C: juist
1. De som van de waarnemingsgetallen delen door het aantal.
2. hoogste – laagste waarneming
3. derde kwartiel – eerste kwartiel
4. -
5. Zie hiernaast.
6. Van elk waarnemingsgetal verschil van het gemiddelde berekenen en dit kwadrateren.
  De som van al die kwadraten delen door het aantal waarnemingsgetallen, je krijgt dan de variantie.
  Tenslotte de wortel trekken uit de variantie levert de standaardafwijking op.
7. 5 cm
8. Vanuit de klassenmiddens.
9. Opnieuw vanuit de klassenmiddens. Zowel het gemiddelde als de standaardafwijking kunnen afwijken van de werkelijke waarden. Dit komt omdat nu alleen nog de klassenmiddens worden gebruikt en dat zijn niet de werkelijke waarnemingen.
10. Het klassenmidden ligt nu aan het einde van een levensjaar, bij je verjaardag.
3. Zie hiernaast.
4. Je controle is dat de gevonden waarden voor gemiddelde en standaardafwijking niet veel verschillen van die bij a en b.
1. ziekenhuis A: gemiddelde = 166 cm en mediaan = 160 cm
  ziekenhuis B: gemiddelde = 166 cm en mediaan = 160 cm
2. Nee, bij ziekenhuis B liggen de getallen verder uit elkaar.
1. plaats A: gemiddelde = 60 mm, mediaan = 60 mm
  plaats B: gemiddelde = 60 mm, mediaan = 60 mm
2. A
3. De variatiebreedte in A is 80 mm, de variatiebreedte in B is 20mm, dus ja.
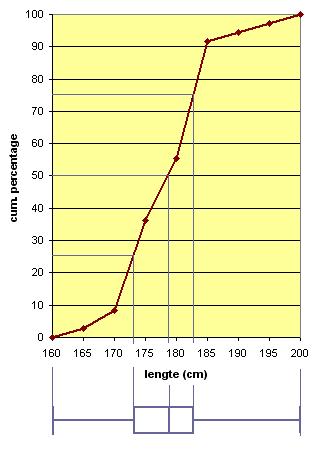
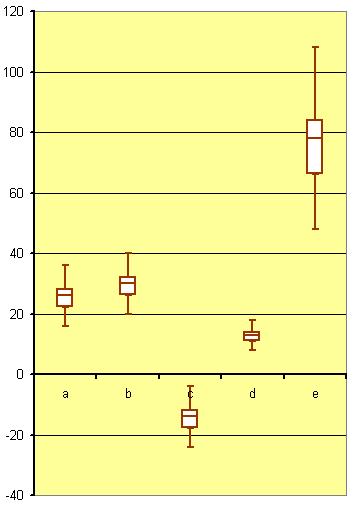
1. De boxplot (a,b en c) blijft dezelfde vorm houden en de afstanden tussen de kengetallen (maximum, minimum, eerste en derde kwartiel, mediaan) blijven gelijk. De boxplot verschuift in zijn geheel langs de as.
2. De afstanden tussen de kengetallen worden vergroot of verkleind met het vermenigvuldigingsgetal. Dit betekent dat de boxplot (d,e) vergroot of verkleind wordt.
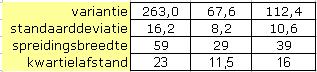
1. Tot op de millimeter nauwkeurig. De lengte 3,0 hoort bij de tweede klasse.
2. De klasse `12,0 - < 15,0`, die bevat het grootste aantal wormen.
3. -
4. In de klasse `9,0 - < 12,0`.
  Je kunt de mediaan niet bepalen, want de losse waarnemingen zijn niet bewaard. M.b.v. de cumulatieve frequentiepolygoon kun je de mediaan schatten: ongeveer 11,8.
5. gemiddelde `~~ 11,79`, standaardafwijking `~~ 4,92`
1. De linker tabel:
  De gemiddelde besteding per klant is ongeveer `112,50`.
  De modale klasse is `100 - < 150`.
  Mediaan is ongeveer 125 en `Q_1 ~~ 75`, `Q_3 ~~ 125` De rechter tabel:
  De gemiddelde tijd per klant is ongeveer `2,25` minuten.
  De modale klasse is `1 - < 2`.
  De mediaan is ongeveer 2,5 en `Q_1 ~~ 1,5`, `Q_3 ~~ 2,5`.
2. Bij de linker verdeling is de standaardafwijking ongeveer 56,1 en bij de rechter is de standaardafwijking ongeveer 1,17.
3. -
4. Er zijn gemiddeld `150000/(112,50) ~~ 1333` klanten per week. (Omzet delen door gemiddelde besteding per klant). Elke klant heeft een gemiddelde 2,25 minuten tijd. Er is in totaal 2,25 maal 1333 minuten aan kassawerk. Dit is 3000 minuten. Met een overcapaciteit van 25% moet je dit getal vermenigvuldigen met 1,25 om te weten hoeveel tijd de supermarkt aan caissières nodig heeft. Dit is `(1,25 * 3000)/60 = 62,5` uur aan kassawerk. Er zijn dus 1,64 caissières nodig.
1. Zie hiernaast.
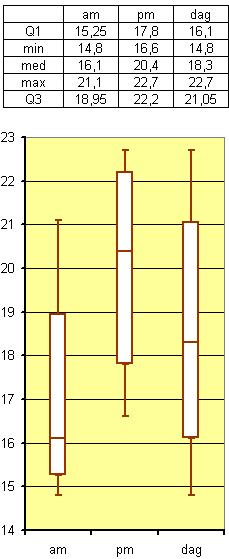
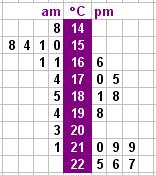
3. a.m.: gemiddelde `~~ 17,0^o`C en standaarddeviatie `~~ 2,1^o`C
  p.m.: gemiddelde `~~ 20,0^o`C en standaarddeviatie `~~ 2,2^o`C
4. dag: gemiddelde `~~ 18,6^o`C en standaarddeviatie `~~ 2,6^o`C
5. 's Morgens is het gemiddeld kouder dan 's middags en 's avonds. Het gemiddelde over de gehele dag is het gemiddelde van beide gemiddelden per dagdeel (evenveel metingen per dagdeel).
  De temperaturen van p.m. liggen kennelijk wat meer gespreid dan die van a.m.
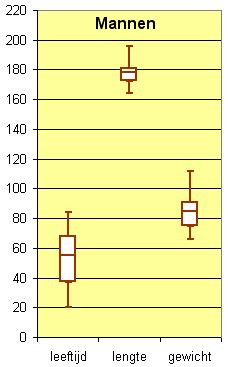
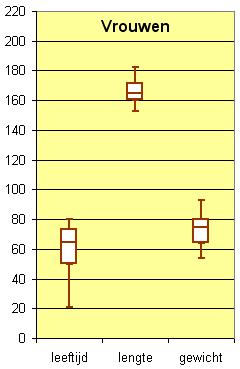
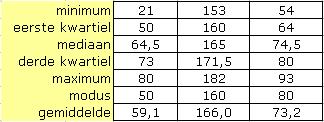
1. Gemiddelde lengte ongeveer 171 cm.
  Mannen zijn gemiddeld 176 cm en vrouwen gemiddeld 164 cm.
2. 198 cm, bezwaar: onnodig hoge kosten aan materiaal en er kan toch wel een langere man ooit moeten worden opgenomen.
3. 50% van 278 is 139. Bedlengte 171 cm.
4. 145 mannen: voor de helft bedden van 176 cm en de 50% grootste mannen bedden van b.v. 200 cm.
  133 vrouwen: voor de helft bedden van 165 cm en voor de 50% grootste vrouwen bedden van b.v. 185 cm.
1. -
2. gemiddelde temperatuur in 2006: 11,2 graden
  gemiddelde temperatuur in 1986: 9,0 graden
  2006 was dus warmer dan 1986.
3. gemiddelde wintertemperatuur in 1988: 5,0 graden
  gemiddelde wintertemperatuur in 2003: 2,4 graden
  de winter van 1988 was dus warmer.
`(53 + p)/7 = 9` geeft `p = 10`.
1. `(20 * 6,6 + x * 8,1)/(20 + x) = 7,5` geeft `x = 30`. Dus 30 leerlingen in H4B.
2. `(x * 6,4 + (20 - x) * 6,9)/(20) = 6,6` geeft `x = 12`. Dus 12 leerlingen in H4A.
`(text(melk zwartbont) + text(melk roodbont))/(text(aantal zwartbont) + text(aantal roodbont)) = 22` L/dag.
Dit geeft:
`(24 * x + 21,55 * (120 - x))/120 = 22` en daaruit vind je `x = 22`.
1. Niet alle klassen zijn even goed. Zit je in een goede klas, dan is je score lager dan wanneer je in een minder goede klas zit. En dit terwijl je prestatie dezelfde is.
2. Zie a.
3. De mediaan.
4. Bij 0% hoort een Citoscore van 500 en bij 100% hoort een Citoscore van 550.
  Bij 537 hoort dus een Citoscore van `37/50 = 74`%.
1. Het gemiddelde aantal personen per huishouden is `141/58 ~~ 2,4`.
2. `((26 * 1 + 14 * 2 + 6 * 3) * 26 + (25 * 1 + 16 * 2 + 4 * 3) * 18,2)/141 ~~ 22,2`
3. `(18 * 26 + x + x + 5)/20 = 27` geeft `x = 33,5`.
  De één is 33,5 en de ander 38,5 jaar.
4. kleinste: 10 huishoudens van 1 persoon weg dus `131/48 ~~ 2,7`
  grootste: 1 huishouden van 6, 2 van 5 en 7 van 4 weg dus `(141 – 6 – 10 – 28)/48 ~~ 2,0`
1. Leeftijd: mediaan.
  Lengte, gewicht en zakgeld: gemiddelde.
  Favoriete drankje en vervoermiddel: modus.
2. Leeftijd: kwartielafstand en spreidingsbreedte.
  Lengte, gewicht en zakgeld: standaarddeviatie.
  Favoriete drankje en vervoermiddel: geen.
3. Doorsnee feetsganger is 16-17 jaar, 181 cm lang, drinkt cola, weegt 71 kg, heeft € 22,13 zakgeld en komt met de fiets.
1. Het modale salaris is ongeveer 30.000 euro/jaar.
2. De mediaan is groter dan de modus want rechts van 30.000 euro/jaar zit een groter gebied onder de grafiek dan links ervan. De mediaan moet zo zitten dat links en rechts een even groot gebied (50% van de werknemers) zit.
1. Het gemiddelde is ongeveer 26,1 seconden, de mediaan is 25 en de modus is 21.
2. De spreidingsbreedte is `42 - 18 = 24` en de standaardafwijking is ongeveer 6,0.
3. Minimum is 18, maximum is 42. De kwartielen zijn `Q_1 = 21` en `Q_3 = 30`.
4. -
5. Het gemiddelde is ongeveer 27,0 seconden en de standaardafwijking is ongeveer 6,2 seconden.
6. De mediaan wordt ongeveer 27 seconden.