Kansen vermenigvuldigen

Inleiding

Je hebt kennis gemaakt met regels voor de kansrekening. Vooral als het gaat om grotere hoeveelheden (52 verschillende speelkaarten) en meerdere trekkingen zijn dergelijke regels nuttig.
Daarom leer je nu wanneer je kansen mag vermenigvuldigen. Hierbij is het vaasmodel weer erg handig.

Je leert nu:

Je kunt al:

Verkennen

Een volledig kaartspel kent 52 kaarten, van elke "kleur" evenveel.
Je trekt aselect uit zo'n kaartspel twee kaarten.

> Bereken de kans op twee azen.
> Bereken de kans op een hartenkaart en een aas.

Uitleg

Je trekt aselect uit een volledig kaartspel twee kaarten. Je kunt dit opvatten als tegelijk twee kaarten trekken of als twee kaarten na elkaar trekken maar zonder terugleggen.
Dit betekent dat de trekking van de tweede kaart afhankelijk is van die van de eerste kaart: bij de tweede trekking is er een kaart minder om uit te kiezen.
De kans op een aas bij de eerste kaart is `4/52`.
De kans op een aas bij de tweede kaart is `3/51`.
Hierbij past een kansboom met twee lagen.
De kans op twee azen is P(2 azen) = `4/52*3/51 = 12/572`.

Je ziet dat je niet zonder meer de kans op twee azen kunt berekenen door de kans op één aas met zichzelf te vermenigvuldigen. Dat gaat wel als het om trekking met terugleggen gaat, maar niet als het om trekking zonder terugleggen gaat. Dan moet je er rekening mee houden dat bij elke volgende trekking de kansen afhangen van wat er eerder is gebeurd, steeds komen er minder kaarten en het is ook nog van belang wat er is getrokken.
Voor de kans op twee azen bij trekking zonder terugleggen geldt:
P(2 azen) = P(aas) · P(aas|eerste keer aas).
P(aas|eerste keer aas) is een voorwaardelijke kans.
Bij het berekenen ervan moet je er rekening mee houden wat er eerder is gebeurd.

‡

Opgaven

  1. Uit een compleet spel speelkaarten worden aselect en met terugleggen twee kaarten getrokken.
    1. Waarom is de tweede trekking van de tweede kaart afhankelijk van de eerste trekking?
    2. Wat is de kans dat je de eerste keer een harten- en de tweede keer een schoppenkaart trekt?
    3. Wat is de kans dat op een harten- en een schoppenkaart?
    4. Wat is een voorwaardelijke kans?
    5. Bereken de volgende voorwaardelijke kans: P(tweede trekking een schoppenkaart | eerste trekking een hartenkaart).
    6. Wat is de kans op twee azen?
    7. Wat is de kans op een vrouw en een heer?

Theorie

Is G1 een gebeurtenis bij een kansexperiment en G2 een gebeurtenis bij een tweede kansexperiment en zijn de kansen van het tweede experiment onafhankelijk van de uitkomst van het eerste, dan is:

P(G1 en G2) = P(G1) · P(G2).

In het vaasmodel is dit het geval als je met terugleggen meerdere balletjes trekt.

Is G1 een gebeurtenis bij een kansexperiment en G2 een gebeurtenis bij een tweede kansexperiment en zijn de kansen van het tweede experiment afhankelijk van de uitkomst van het eerste, dan is:

P(G1 en G2) = P(G1) · P(G2|G1).

In dit geval is P(G2|G1) een voorwaardelijke kans, namelijk de kans op G2 onder de voorwaarde dat G1 eerst heeft plaatsgevonden.
In het vaasmodel is dit het geval als je zonder terugleggen meerdere balletjes trekt.

De regel P(G1 en G2) = P(G1) · P(G2|G1) heet wel de algemene productregel voor kansen omdat hij ook geldig is voor onafhankelijke gebeurtenissen.
Dan is namelijk P(G2|G1) = P(G2).

‡

Voorbeeld 1

Uit een vaas met 6 rode en 4 blauwe knikkers worden met teruglegging twee knikkers getrokken.
Hoe groot is de kans op een rode en een blauwe knikker?

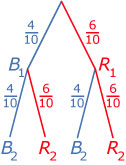
Antwoord

Het maakt bij de tweede trekking niet uit of de eerst getrokken knikker rood of blauw was. Door het terugleggen is immers de oorspronkelijke situatie weer hersteld. De tweede trekking is daarom onafhankelijk van de eerste.

Je kunt dus de productregel voor onafhankelijke kansen gebruiken:

Beide gebeurtenissen sluiten elkaar uit, dus P(R en B) = `24/100 + 24/100 = 48/100`.

‡

Voorbeeld 2

Uit een vaas met 6 rode en 4 blauwe knikkers worden zonder teruglegging twee knikkers getrokken.
Hoe groot is de kans op een rode en een blauwe knikker?

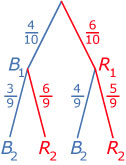
Antwoord

Het maakt bij de tweede trekking verschil of de eerst getrokken knikker rood of blauw was. Door niet terug te leggen is immers de oorspronkelijke situatie gewijzigd. De tweede trekking is daarom afhankelijk van de eerste.

Je kunt dus de productregel voor afhankelijke kansen gebruiken:

Beide gebeurtenissen sluiten elkaar uit, dus P(R en B) = `24/90 + 24/90 = 48/90`.

‡

Voorbeeld 3

Uit een vaas met 6 rode en 4 blauwe knikkers worden zonder teruglegging twee knikkers getrokken.
Hoe groot is de kans dat de tweede knikker rood is?

Antwoord

Het maakt bij de tweede trekking verschil of de eerst getrokken knikker rood of blauw was. Door niet terug te leggen is immers de oorspronkelijke situatie gewijzigd. De tweede trekking is daarom afhankelijk van de eerste.

De gevraagde kans is
P(R2) = P(R1 en R2) + P(B1 en R2) =
= P(R1) · P(R2|R1) + P(B1) · P(R2|B1) = `6/10 * 5/9 + 4/10 * 6/9 = 54/90`.

‡

Voorbeeld

Uit een vaas met 6 rode en 4 blauwe knikkers worden zonder teruglegging twee knikkers getrokken.
Je krijgt alleen de tweede knikker te zien, die is blauw.
Hoe groot is de kans dat de eerste knikker rood is?

Antwoord

Het maakt bij de tweede trekking verschil of de eerst getrokken knikker rood of blauw was. Door niet terug te leggen is immers de oorspronkelijke situatie gewijzigd. De tweede trekking is daarom afhankelijk van de eerste.

De gevraagde kans is P(R1|B2).
Omdat P(B2) = P(R1 en B2) + P(B1 en B2) =
= P(R1) · P(B2|R1) + P(B1) · P(B2|B1) = `6/10 * 4/9 + 4/10 * 3/9 = 36/90`
is gemiddeld in 36 van de 90 trekkingen de tweede bal blauw.
In 4 · 6 = 24 van die trekkingen was de eerste bal rood.
De gevraagde kans is daarom `24/36`.

Merk op dat je deze kans kunt berekenen vanuit P(B2) en P(R1 en B2):
`text(P)(R_1 | B_2) = (text(P)(R_1 text( en ) B_2))/(text(P)(B_2))`.
Ga na dat dit netjes past bij de algemene productregel voor afhankelijke gebeurtenissen.

‡

Opgaven

  1. Bekijk Voorbeeld 1.
    1. Bereken de kans op twee blauwe knikkers.
    2. Bereken de kans op twee rode knikkers.
    3. Waarom is hier geen sprake van voorwaardelijke kansen?

  2. Bekijk Voorbeeld 2.
    1. Bereken de kans op twee blauwe knikkers.
    2. Bereken de kans op twee rode knikkers.
    3. Bereken de voorwaardelijke kans `text(P)(B_2|B_1)`.
    4. Waarom is het berekenen van `text(P)(B_2|R_2)` onmogelijk?

  3. In Voorbeeld 3 gaat het om de tweede knikker. Hoe groot is de kans dat de tweede knikker blauw is?

  4. In Voorbeeld 4 gaat het om de eerste knikker.
    1. Hoe groot is de kans dat de eerste knikker blauw is?
    2. Stel je nu voor dat de tweede knikker rood is. Hoe groot is dan de kans dat de eerste knikker blauw is?

  5. Je hebt nu een vaas met 7 rode, 5 witte en 8 blauwe knikkers. Je trekt hieruit in één greep drie knikkers.
    1. Bereken de kans op 3 rode knikkers.
    2. Bereken P(derde knikker is blauw | eerste twee knikkers zijn rood).
    3. Bereken P(derde knikker is blauw en eerste twee knikkers zijn rood).
    4. Bereken de kans op 2 rode knikkers.
    5. Bereken de kans op drie knikkers van verschillende kleur.

  6. Voorwaardelijke kansen komen geregeld voor als je kansen berekent bij gegeven tabellen. Een voorbeeld is een onderzoek naar de Mantoux-test onder een grote groep personen. De Mantoux-test is een huidtest die wordt gebruikt om na te gaan of iemand tuberculose heeft. Vrijwel alle personen die aan tuberculose lijden laten een reactie zien op deze huidtest, maar ook een zeer klein deel van de personen die niet aan tuberculose lijden vertonen die reactie.
    De tabel laat dat zien:

    Mantoux-test tuberculose geen tuberculose
    reactie 98 99 197
    geen reactie 2 9801 9803

    		100 999 10.000

    1. Bereken in vier decimalen nauwkeurig de kans dat iemand die een reactie vertoont op de Mantoux-test ook inderdaad aan tuberculose lijdt.
    2. Bereken in vier decimalen nauwkeurig de kans dat iemand die geen reactie vertoont toch aan tuberculose lijdt.

Verwerken

  1. Bij een wandeltocht door vochtig terrein zijn je sokken nat geworden. Onder in je rugzak heb je, los door elkaar, 8 droge sokken van 4 verschillende paren. Je trekt er één sok uit, en dan steeds weer een tot je de bijpassende sok hebt gekregen. Het is verstandig als je niet teruglegt.
    1. Wat is de kans dat je precies bij de vierde sok de bij de eerste passende trekt?
    2. Wat is de kans dat de tweede of de derde sok al de goede is?

  2. De kans op tenminste één 6 bij vier keer gooien met een dobbelsteen is groter dan 50%.
    1. Laat zien dat dit inderdaad zo is.
    Chevalier de Méré dacht daarom (in 1654) dat hij ook meer dan 50% kans had op dubbel zes als hij `6*4 = 24` keer met twee dobbelstenen gooide, maar hij kwam bedrogen uit. Zijn vriend Pascal moest hem uit de droom helpen.
    1. Bereken die kans op dubbel 6 in procenten, in twee decimalen nauwkeurig.
    2. Hoe vaak moet je minstens gooien opdat de kans groter is dan 50%?

  3. Bij een bepaalde ziekte kunnen twee verschillende medicijnen worden voorgeschreven: medicijn A of medicijn B. In principe wordt altijd (het beste) medicijn A voorgeschreven, maar 10% van de patiënten reageert daar allergisch op en krijgt dan medicijn B. Medicijn A zorgt in 95% van de gevallen voor genezing, medicijn B in 75% van de gevallen.
    Iemand krijgt deze ziekte en geneest. Hoe groot is de kans dat hij medicijn B heeft gekregen?

  4. In West-Europa heeft 40% van de bevolking bloedgroep A, 10% bloedgroep B, 5% bloedgroep AB en 45% bloedgroep O. Voor de Rhesus-factor geldt: 85% is Rh-positief en 15% is Rh-negatief, ongeacht de bloedgroep waartoe men behoort.
    1. Bereken het percentage West Europeanen dat bloedgroep A heeft en Rh-positief is.
    2. Bereken het percentage West Europeanen dat bloedgroep O heeft en Rh-negatief is.
    3. Bereken het percentage West Europeanen dat Rh-negatief is en niet bloedgroep O heeft.
    4. Welke van de acht combinaties van bloedgroep en Rh-factor is het zeldzaamst?

  5. In een doos zitten tien kaarten, elk met een cijfer erop. Op 1 kaart staat een 1, op 2 kaarten een 2, op 3 kaarten een 3 en op 4 kaarten een 4. Je trekt zonder terugleggen 4 kaarten en legt die van links naar rechts naast elkaar. Je ziet dan een getal van 4 cijfers.
    1. Wat is de kans dat dit getal 1234 is?
    2. Wat is de kans dat dit getal 4321 is?
    3. Wat is de kans dat dit getal 3344 is?
    Laat `E` het getal zijn dat door de eerste twee cijfers wordt voorgesteld, `T` het getal dat door de laatste twee cijfers wordt voorgesteld.
    1. Bij a en b heb je (hopelijk) dezelfde antwoorden gekregen. Verklaar waarom elk van de getallen die je met de cijfers 1, 2, 3 en 4 kunt schrijven dezelfde kans heeft.
    2. Bereken `text(P)(T = 34 | E = 12)` en `text(P)(T = 12 | E = 34)`.
    Eén kaart is stiekem door iemand gemerkt.
    1. Wat is de kans dat die kaart op uiterst links terechtkomt?
    2. Voor de kans dat de gemerkte kaart als derde wordt getrokken kun je beter niet rekenen maar nadenken. Resultaat?
    3. Test de productregel door na te gaan of je daarmee hetzelfde resultaat krijgt.
    4. Wat is de kans dat het getal begint met een 3? Eindigt met een 3? Begint en eindigt met een 3?

  6. De winnaar van een quiz mag uit drie dozen er een kiezen. De dozen zien er hetzelfde uit, maar in één ervan zit de hoofdprijs, de andere twee zijn leeg. Na die keuze wijst de spelleider een andere doos aan en zegt (naar waarheid) dat die leeg is. De winnaar mag nu nog zijn keuze veranderen.
    1. Bereken de winstkans in het geval dat hij niet wisselt.
    2. Bereken de winstkans in het geval dat hij wisselt.

  7. De verkiezing voor de Tweede Kamer in januari 2003 leverde de volgende zetelverdeling op. Bij 'nieuw' staat het aantal leden dat voor het eerst in de Tweede Kamer zit. K is een willekeurig kamerlid.

    TK 2003 CDA PvdA VVD SP LPF Gr.L. D'66 Chr.U. SGP Kamer
    mannen 29 23 20 5 6 3 4 3 2 95
    vrouwen 15 19 8 4 2 5 2 0 0 55
    totaal 44 42 28 9 8 8 6 3 2 150
    nieuw(m) 1 10 3 0 0 0 0 0 0 14
    nieuw(v) 0 8 5 0 2 0 1 0 0 16

    1. Bepaal de kans dat K een vrouw is.
    2. Wat is de kans dat K een vrouw is als K lid is van het CDA? Lid is van de PvdA? Lid is van het CDA of van de PvdA?
    3. Bepaal door tellen en ook met de productregel de kans dat K een vrouwelijk lid van het CDA is.
    4. Hoe groot is de kans dat een vrouwelijk kamerlid bij de VVD hoort? Niet bij de VVD hoort? Bij de SGP hoort?
    5. Bepaal voor elke politieke partij de voorwaardelijke kans P(K is nieuw | K is lid van die partij).
    6. Bepaal voor elke politieke partij de kans P(K is nieuw en K is lid van die partij).
    7. Welke kans is het grootste, de kans dat een nieuw kamerlid een vrouw is of de kans dat een vrouwelijk kamerlid nieuw is?

Testen

  1. 60% van de artikelen die een fabriek maakt is van soort A, 40% is van soort B. Er gaat wel eens iets mis. Van de artikelen van soort A moet 1% worden afgekeurd. Voor soort B is dat zelfs 2%.
    1. Wat is de kans dat een aselect gekozen artikel van soort A is en wordt afgekeurd?
    2. Wat is de kans dat een aselect gekozen artikel van soort B is en wordt goedgekeurd?
    3. Wat is de kans dat een aselect gekozen artikel wordt afgekeurd?
    4. Je kunt de productregel gebruiken om de kans te berekenen dat een afgekeurd artikel van soort B is. Doe dit.

  2. Je hebt een vaas met 1200 balletjes, 500 rode, 400 witte en 300 blauwe. Bij elke kleur zijn 200 van de balletjes van hout, de andere zijn van plastic. Het verschil is niet te voelen. `B` is een aselect uit de vaas gepakt balletje.
    1. Bepaal P(`B` is rood | `B` is van hout) en P(`B` is van hout | `B` is rood).
    2. Bepaal P(`B` is rood of `B` is van hout) en P(`B` is rood en `B` is van hout)?
    3. Bepaal P(`B` is blauw of `B` is van plastic `B` is niet wit) en P(`B` is blauw of `B` is van plastic `B` is wit).

  3. In een doos zitten 900 briefjes met daarop de getallen 100, 101, 102, ... , 999.
    1. Op hoeveel briefjes in de doos komt het cijfer 0 voor als laatste cijfer? En als middelste cijfer? Reken na dat op 171 briefjes een 0 voorkomt.
    2. Op hoeveel briefjes in de doos komt het cijfer 9 voor als laatste cijfer? Als middelste cijfer? Als eerste cijfer? Onder de twee laatste cijfers?
    3. Controleer dat op 252 briefjes een 9 voorkomt. (Je kunt het uitrekenen met de somregel als je eerst nagaat hoeveel briefjes een 9 als linker cijfer hebben en ook tenminste één 9 bij de twee rechter cijfers. Je kunt ook een manier gebruiken die in opgave 23 is uitgelegd).
    4. Je trekt uit die vaas een briefje A, en zonder terugleggen een tweede briefje B. Bereken P(A bevat een 0), P(B bevat een 0 | A bevat een 0) en (in procenten) P(B bevat een 0 en A bevat een 0).
    5. Bereken P(A bevat een 9), P(B bevat een 9 | A bevat een 9) en (in procenten) P(B bevat een 9 en A bevat een 9).
    6. Ga na hoeveel briefjes er in de vaas zitten waarop een 0 én een 9 staat.
    7. P(A bevat een 9 | A bevat een 0) kun je berekenen door de productregel te gebruiken, hoe? Reken hem uit.
    8. Je kunt P(A bevat een 0 en B bevat een 9) het best uitrekenen met een kansboom door die met vier takken te laten beginnen: A bevat een 0 en geen 9, een 0 en een 9, een 9 en geen 0 of noch een 0, noch een 9. Voer de berekening uit.
    9. Gebruik het resultaat van h om P(B bevat een 9 | A bevat een 0) te berekenen.

  4. Op een school is onderzocht hoeveel leerlingen er roken. In de tabel vind je de resultaten van dat onderzoek.

    rookgedrag mannen vrouwen
    roken 105 134 239
    niet roken 475 486 961

    		580 620 1200

    1. Bereken in vier decimalen nauwkeurig de kans dat een willekeurige leerling van deze school rookt.
    2. Bereken in vier decimalen nauwkeurig de kans dat een willekeurig meisje van deze school rookt.
    3. Bereken in vier decimalen nauwkeurig de kans dat een willekeurige rokende leerling van deze school een meisje is.