Machten en faculteiten

Inleiding

Bij het systematisch tellen heb je tot nu toe vooral gewerkt met diagrammen. Eigenlijk gaat dat alleen als het aantal mogelijkheden niet al te groot is. Want als je bijvoorbeeld met drie of meer dobbelstenen gaat gooien, dan wordt het aantal even waarschijnlijke uitkomsten al snel zo groot, dat een boomdiagram niet meer te maken is. Wegendiagrammen zijn dan nog wel te maken, maar daarin kun je weer niet zo gemakkelijk de afzonderlijke gunstige mogelijkheden tellen. Kortom: tijd voor het werken aan telsystemen. Daarbij is als eerste belangrijk om onderscheid te maken tussen situaties waarin herhaling optreedt en situaties waarin dat niet zo is.

Je leert nu:

• werken met machten als je mogelijkheden telt in situaties waarin herhaling optreedt;
• werken met faculteiten als je mogelijkheden telt in situaties waarin steeds een mogelijkheid wordt afgestreept;
• werken met faculteiten op de rekenmachine.

Je kunt al:

• werken met tabellen en diagrammen om mogelijkheden te tellen;
• werken met kansen.

Verkennen

Gironummers en banknummers bestaan uit een groot aantal cijfers. Neem eens aan dat elk gironummer uit 7 cijfers bestaat en dat op elke positie elk cijfer kan voorkomen.

> Hoeveel gironummers kun je zo maken?
> Het eerste cijfer mag geen 0 zijn. Hoeveel gironummers kun je nu nog maken?
> Hoeveel gironummers zijn er met allemaal verschillende cijfers?

Uitleg

Stel je voor dat je wilt berekenen hoeveel verschillende pincodes mogelijk zijn.
De eerste vraag die je kunt stellen: mag ik cijfers herhalen of niet?

Als bij de pincode (van 4 cijfers) herhaling van de cijfers is toegestaan, dan kun je de situatie weergeven in dit wegendiagram:

Het aantal mogelijkheden is: 10 × 10 × 10 × 10 = 10⁴.
Hier bereken je het aantal mogelijkheden met behulp van machten.
Dat komt omdat je cijfers mag herhalen.

Maar als je allemaal verschillende cijfers wilt hebben...

Als bij de pincode van 4 cijfers herhaling van cijfers niet is toegestaan dan ziet het wegendiagram met alle mogelijkheden er zo uit:

Het aantal mogelijkheden is: 10 × 9 × 8 × 7 = 5040.

Omdat het berekenen van dergelijke aflopende vermenigvuldigingen nogal tijdrovend is, hebben wiskundigen daarvoor het begrip faculteit ingevoerd.

10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 wordt 10 faculteit genoemd en genoteerd als 10!.
Je rekenmachine beschikt over een functie om faculteiten te berekenen.
Controleer maar eens dat 10! = 3628800.
Ga ook na dat: 6! = 720, dat 1! = 1 en dat 0! = 1.

Je kunt 10 × 9 × 8 × 7 als volgt uitrekenen met behulp van faculteiten:

`10xx9xx8xx7=(10*9*8*7*6*5*4*3*2*1)/(6*5*4*3*2*1)=(10!)/(6!)`

Ga na, dat dit inderdaad 5040 oplevert.
Het werken met faculteiten is vooral handig als het om grote aantallen gaat.

‡

Opgaven

1. Bekijk beide pagina's van de Uitleg.
   Je hebt zes verschillende gekleurde kaartjes. Op die kaartjes wil je de letters A, B, C, D, E en F zetten.
   1. Op hoeveel manieren kan dat als je op meerdere kaartjes dezelfde letter toelaat?
   2. Op hoeveel manieren kan dat als elk kaartje een verschillende letter moet krijgen?


2. Nu gebruik je alle 26 letters van het alfabet. En je hebt nog steeds 6 verschillend gekleurde kaartjes.
   1. Op hoeveel manieren kun je er letters op zetten als je op meerdere kaartjes dezelfde letter toelaat?
   2. Op hoeveel manieren kun je er letters op zetten als elk kaartje een verschillende letter moet krijgen?

Theorie

Als je r elementen kiest uit n beschikbare elementen en herhaling is toegestaan dan heb je n^r mogelijkheden.

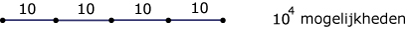
Als herhaling niet is toegestaan, dan krijg je te maken met vermenigvuldiging van een rij getallen die steeds met één verminderd. De vermenigvuldiging van de aflopende rij opeenvolgende getallen n tot en met 1 wordt n-faculteit genoemd.
Dit schrijf je als n!, dus n! = n · (n – 1) · (n – 2) · ... · 3 · 2 · 1.
Afgesproken is dat 0! = 1.
De rekenmachine heeft een functie om faculteiten te berekenen.

Als je n elementen kiest uit n beschikbare elementen en herhaling is niet toegestaan dan heb je n! mogelijkheden. Dit heet het aantal permutaties van n elementen.

Als je r elementen kiest uit n beschikbare elementen en herhaling is niet toegestaan dan heb je `(n!)/((n-r)!)` mogelijkheden. Dit heet het aantal permutaties van r elementen uit n elementen.

‡

Voorbeeld 1

In Nederland bestaat een bepaalde categorie kentekenplaten (op auto's) uit twee cijfers gevolgd door vier letters. Neem aan dat alle letters en cijfers mogen worden gebruikt.
Hoeveel kentekens kun je dan maken, als herhaling van letters en cijfers is toegestaan?

Antwoord

Dit kun je berekenen met machten. Voor elk kenteken heb je twee cijfers nodig en er zijn 10 verschillende cijfers. Je hebt dan totaal 10² = 100 verschillende mogelijkheden.

Voor elk kenteken heb je vier letters nodig en er zijn 26 verschillende letters. Je hebt 26⁴ = 456976 verschillende mogelijkheden voor de letters.

In totaal zijn er dus 10² · 26⁴ = 45.697.600 mogelijke kentekenplaten.
Dat is meer dan 45 miljoen!

(In werkelijkheid zijn het er minder omdat niet alle letters worden gebruikt en sommige letters alleen voor speciale voertuigen, zie ook bij de site van de RijksDienst Wegverkeer.)

‡

Voorbeeld 2

In Nederland bestaat een bepaalde categorie kentekenplaten (op auto's) uit twee cijfers gevolgd door vier letters. Neem aan dat alle letters en cijfers mogen worden gebruikt.
Dit kenteken kent allemaal verschillende tekens, hoe groot is de kans daar op?

Antwoord

In het voorgaande voorbeeld kun je zien dat er 10² · 26⁴ = 45.697.600 kentekenplaten mogelijk zijn als de tekens ook mogen worden herhaald.

Mogen de tekens niet worden herhaald, zijn dat er 10 · 9 · 26 · 25 · 24 · 23 = 32.292.000.

De gevraagde kans is `32292000/45697600~~0,7067`, dus ongeveer 71%.

‡

Voorbeeld 3

Tijdens de finale van de 100 meter hardlopen op de Olympische Spelen strijden 8 lopers om 3 medailles. De lopers zijn allemaal topatleten. Je neemt aan dat ze volkomen gelijkwaardig zijn.

Op hoeveel manieren kunnen de medailles worden verdeeld?

Antwoord

Stel je een wegendiagram voor. Voor de eerste positie zijn 8 mogelijke kandidaten, voor de tweede dan nog 7 en voor de derde nog 6.

Er zijn `8*7*6 = (8!)/(5!) = 336` mogelijke uitslagen.
Dit is het aantal mogelijke permutaties van 3 elementen uit 8 elementen.

Je grafische rekenmachine kent hiervoor een speciale functie.

‡

Opgaven

3. Zie Voorbeeld 1.
   Nummerborden van een bepaalde generatie auto’s bestaan uit twee letters, weer twee letters en tenslotte twee cijfers. Bijvoorbeeld DB-TR-69. De letters I, O en Q worden niet gebruikt. Ga ervan uit dat verder alle letters en alle cijfers kunnen worden gebruikt. Zie ook Voorbeeld 1 en Voorbeeld 2.
   1. Hoeveel van deze nummerborden zijn er dan mogelijk?
   2. Hoeveel van deze nummerborden zijn er mogelijk als je geen letters en cijfers mag herhalen?


4. Uit een aanbod van 40 boeken moet een jury nummer 1, nummer 2 en nummer 3 kiezen. Bekijk Voorbeeld 3.
   Wanneer de jury op goed geluk deze boeken uitkiest, zonder verder naar de inhoud te kijken, hoeveel verschillende keuzes zijn er dan mogelijk?
   


5. Lees in de Theorie na wat er wordt verstaan onder "permutaties" en "variaties". Let goed op het verschil tussen beide.
   1. Omschrijf wat je verstaat onder het aantal permutaties van 10 elementen. Bereken dit aantal.
   2. Wat versta je onder het aantal permutaties van 3 uit 10 elementen? Bereken dat aantal.
   3. Hoeveel bedraagt het aantal permutaties van 5 uit 100 elementen?


6. Je maakt getallen met de cijfers 4, 5, 6, 7 en 8.
   1. Je maakt getallen van vijf cijfers. Hoeveel getallen zijn er mogelijk?
   2. Je maakt getallen van vijf verschillende cijfers. Hoeveel getallen zijn er mogelijk?
   3. Je maakt getallen van drie cijfers. Hoeveel getallen zijn er mogelijk?
   4. Je maakt getallen van drie verschillende cijfers. Hoeveel getallen zijn er mogelijk?
   5. Je maakt getallen van vijf cijfers boven de 65000. Hoeveel kun je er maken?
   6. Je maakt getallen van vijf verschillende cijfers boven de 65000. Hoeveel kun je er maken?

Verwerken

7. In Nederland bestaat de postcode uit vier cijfers, gevolgd door twee letters. Neem aan dat alle cijfers op elk van die vier plaatjes mogelijk zijn. Neem ook aan dat elke letter op elk van die twee plaatsen mogelijk is.
   Hoeveel postcodes zijn er dan in Nederland in totaal mogelijk?
   


8. De tekens van een grafische rekenmachine bestaan uit puntjes: elk teken past in een rechthoekje van 5 bij 7 puntjes. Een teken wordt gemaakt door deze puntjes 'aan' of 'uit' te zetten.
   Hoeveel tekens zijn er zo in principe mogelijk?
   


9. Aan de herenfinale op de steeple-chase doen bij de Olympische Spelen 15 mannen mee. De nummers 1, 2 en 3 komen op het erepodium.
1. Op hoeveel manieren kunnen die ereplaatsen theoretisch worden verdeeld?
2. Hoe groot is de kans op een bepaalde volgorde theoretisch?


10. Een groep van acht personen heeft kaartjes voor een concert gekocht. Ze zitten alle acht naast elkaar op één rij.
    1. Hoeveel verschillende volgordes zijn er mogelijk?
    2. Eén van de acht wil per sé de buitenste van de groep zijn. Op hoeveel verschillende manieren kunnen ze nu nog zitten?
    3. Twee personen willen per sé naast elkaar zitten. Hoeveel verschillende volgordes zijn er nu nog mogelijk?


11. Je werpt met vier dobbelstenen. Je let op het totaal aantal ogen.
    Bereken de kans dat het maximaal aantal ogen 23 of meer is.

Testen

12. Je maakt getallen van vijf cijfers.
    1. Hoeveel verschillende getallen zijn er mogelijk als ieder cijfer op elke positie is toegestaan?
    2. Hoeveel verschillende getallen zijn er mogelijk als de getallen niet met 0 mogen beginnen?
    3. Hoeveel van die getallen zijn er nog mogelijk als alle cijfers verschillend moeten zijn?
    4. Hoeveel getallen zijn er met vijf verschillende cijfers en boven de 43000?


13. Een toets bestaat uit 30 meerkeuzevragen. Op elke meerkeuzevraag kun je uit vier antwoorden kiezen; er is telkens maar één antwoord goed.
    1. Hoeveel mogelijke series antwoorden zijn er?
    2. Je hebt de toets goed voorbereid en je weet 24 antwoorden zeker; de rest moet je gokken. Hoeveel mogelijke series antwoorden zijn er dan nog?
    3. Hoe groot is de kans dat je alle antwoorden goed hebt?


14. In de lottomachine zitten balletjes met de nummers 1 tot en met 41. Er worden één voor één zes balletjes uitgehaald. Het eerst getrokken balletje valt in het eerste bakje, het tweede in het tweede bakje, enzovoorts.
    1. Hoeveel verschillende trekkingen zijn er dan mogelijk?
    2. Hoeveel van deze trekkingen leveren dezelfde zes getrokken ballen op?
    3. Je hebt op je lottoformulier aangekruist 1, 13, 17, 19, 31 en 41. Hoe groot is de kans dat die getallen worden getrokken?