
Experimenteren
Antwoorden bij de opgaven
-
-
10 ogen kun je op drie manieren krijgen, bij 5-5, 6-4 en 4-6
7 ogen kun je op wel zes manieren krijgen, bij 1-6, 6-1, 2-5, 5-2, 3-4 en 4-3
-
Dat kan alleen als je beschikt over een statistiek met zijn ziekte verleden.
-
Door daarvan statistieken te zoeken of zelf bij te houden.
-
Op een gewone dobbelsteen zitten evenveel kant met een even aantal ogen als met een oneven aantal ogen.
Je moet er wel van uit gaan dat de dobbelsteen eerlijk is.
-
Moet je ook baseren op statistieken over voorgaande duels van dezelfde teams en zelfs dan is dit uiterst onbetrouwbaar!
-
18 van de 37 vakjes zijn rood en elk vakje heeft (als alles eerlijk toe gaat) een even grote waarschijnlijkheid.
-
-
`98/600`
-
`997/6000`
-
Ja, het lijkt er op dat alle kansen op de lange duur richting de `1/6` gaan.
-
-
Gewoon proberen...
-
-
-
Vaker proberen.
-
-
-
-
-
-
-
-
Zie het antwoord bij opgave 1a.
-
-
0, 1, 2, 3, 4, 5
-
Er 1 bij op tellen.
-
Randomgetallen genereren van 6*X+1.
-
-
-
Je zou in de buurt van `1/6` moeten uitkomen.
-
Je zou in de buurt van `1/9` moeten uitkomen.
-
-
0,731
-
0,111
-
0,5%
-
-
Totaal 5280, gunstig 432.
De gevraagde kans is `432/5280 ~~ 8`%
-
`432/10000~~4,3`%.
Er zijn 432 kleurenblinde mannen op de 10000 personen (mannen en vrouwen).
Bij a ging het alleen om de kleurenblinde mannen, dus op de 5280 mannen.
-
-
Ja, kan bij eerlijke dobbelsteen.
-
Kan niet, want deze dobbelsteen is oneerlijk.
-
Kan bij eerlijke dobbelsteen.
-
-
Simulatie met toevalsgetallen 1 t/m 4.
-
`1/4`
-
Dat kan op verschillende manieren:
- er zijn 16 mogelijke tweetallen, dus simulatie met toevalsgetallen 1 t/m 16;
- twee 'losse' dobbelstenen, eerste worpen (bijv. 20) als eerste lijst, tweede worpen (ook 20) als tweede lijst.
-
-
Zie figuur.
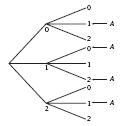
-
Er zijn 9 mogelijke paren, die allemaal even waarschijnlijk zijn
(als ze tenminste niet volgens een bepaalde strategie spelen).
Elk van die mogelijkheden geef je een nummer, 1 t/m 9.
De nummers 2, 4, 6, 8 zijn winst voor A, de rest voor B.
-
Nee, B heeft meer kans.
-
-
-
-
-
-
300
-
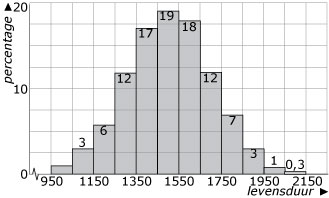
-
`32/300 ~~ 11`%
-
`70/300 ~~ 23`%
-
Dat is een levensduur van minder dan 1350 en meer dan 1650 uur.
Dus ongeveer `68/300 + 70/300 ~~ 46`%.
-
-
`7/18`
-
`29/100`
-
-
Heel vaak met één van die dobbelstenen gooien en bijhouden hoe vaak elk vlakje boven komt.
En daarna zou je dit ook nog met de andere dobbelsteen moeten doen.
-
Omdat bij zo'n simulatie wordt uitgegaan van gelijke kansen voor elk vlakje.
-
-
-
Je zou in de buurt van de `3/16` moeten uitkomen.
-
-
Ongeveer 42,1%.
-
M: 50,3% en L: 12,6%
-
127 stuks S; 151 stuks M; 38 stuks L
-
-
0,118
-
`(21,4)/200 = 0,107`


