Totaalbeeld

Samenvatten

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Discrete wiskunde > Matrices en grafen > Totaalbeeld > Samenvatten

Je hebt nu het onderwerp "Matrices en grafen" doorgewerkt. Er moet een totaalbeeld van deze leerstof ontstaan...
Ga na, of je al de bij dit onderwerp horende begrippen kent en weet wat je er mee kunt doen. Ga ook na of je de activiteiten die staan genoemd kunt uitvoeren. Maak een eigen samenvatting!

31. matrix, kental, rij, kolom, afmetingen — getransponeerde matrix
32. matrixvermenigvuldiging — vierkante matrix, hoofddiagonaal — macht v.e. matrix
33. graaf, knooppunt, verbindingslijn, verbindingsmatrix — (on)gerichte graaf — graad van verbinding — directe wegen, directe-wegen-matrix
34. overgangsgraaf, luswegen — overgangsmatrix, overgangskansen — evenwicht
35. populatievoorspellingsgraaf, generaties, overlevingskansen, geboortecijfers — populatievoorspellingsmatrix of Leslie-matrix

31. matrices optellen, aftrekken en verm. met een getal — matrix transponeren
32. matrices vermenigvuldigen — machten van vierkante matrices
33. bij een ongerichte graaf een verbindingsmatrix maken en de graad van verbinding berekenen — aantallen meerstapsverbindingen in een graaf berekenen — bij een ongerichte graaf een direct-wegen-matrix maken
34. bij een overgangsgraaf een overgangsmatrix maken — onderzoeken of er evenwicht ontstaat in een bepaalde overgangssituatie
35. bij populatiegegevens een populatievoorspellingsgraaf en een populatievoorspellingsmatrix maken en daarmee het verloop ervan voorspellen

Achtergronden

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Discrete wiskunde > Matrices en grafen > Totaalbeeld > Achtergronden

Testen

Opgaven

1. Hieronder zie je een deel van de voedselketen van vogels voor de kust van Long Island (U.S.A.). Zo zie je bijvoorbeeld dat een voorn plankton en waterplanten eet. De voorn wordt onder andere door de ijsvogel gegeten.
   
   
   
   Stel dat er sprake is van een verhoging van de hoeveelheid gif in de waterplanten. Neem aan dat alleen de aangegeven planten en dieren gegeten worden. Met het voedsel wordt ook het vergif doorgegeven.
   1. Mag je een verhoging van de hoeveelheid gif bij alle genoemde vogels verwachten? Licht je antwoord toe.
   Het is mogelijk de bovenstaande voedselketen weer de geven met behulp van matrices. De voedselstromen van P naar F zijn in deze matrix `M` weergegeven:

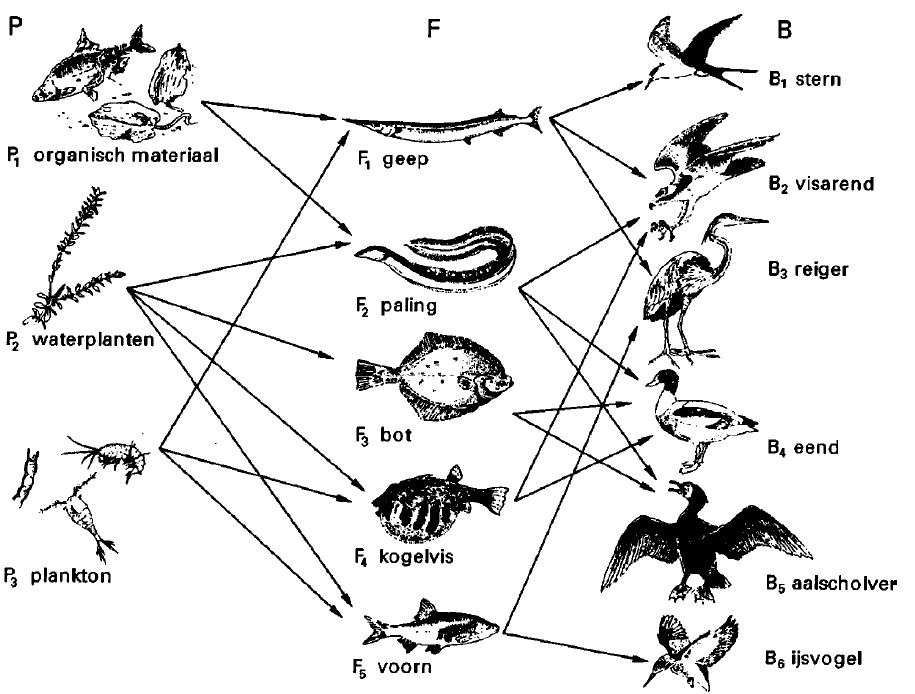
   `M = ((1 , 0 , 1),(1 , 1, 0),(0 , 1 , 0),(0 , 1 , 1),(0 , 1 , 1))`

   Ga er van uit dat de getallen op de bovenste rij aangeven dat P₁ wel, P₂ niet en P₃ weer wel door F₁ wordt gegeten. Verder gaat de tweede rij over F₂, de derde over F₃, enzovoort.
   2. Maak een vergelijkbare matrix `N` die de voedselstromen van F naar B weergeeft. Doe dit zo, dat `M` en `N` kunnen worden vermenigvuldigd.
   3. Vermenigvuldig de matrices `M` en `N` en licht de betekenis van de getallen in deze matrix toe.


2. Een tuinman heeft zaad bewaard van zijn witte en zijn rode rozen. Hij weet dat het zaad van de witte rozen voor 70% weer witte rozen en voor 30% rode rozen oplevert. Het zaad van de rode rozen levert voor 20% witte en voor 80% rode rozen op. Je ziet dat hiernaast in schema.
   1. Teken hierbij een graaf met twee knooppunten.
   2. Stel een bijbehorende overgangsmatrix `R` op.
   3. Het zaad dat de tuinman heeft bewaard was voor 55% afkomstig van witte rozen en voor 45% van rode rozen. Als hij alle zaad laat ontkiemen, hoe is de verdeling dan een jaar later?
   4. Bereken de matrix `R^2`. Welke betekenis heeft deze matrix?
   5. Welke matrix benadert `R^n` als `n` steeds groter wordt? Wat betekent dat voor de verdeling van de kleuren van de rozen?


3. Tussen de vijf Griekse eilanden, Ios, Naxos, Mikonos, Siros en Serifos, bestaan de volgende bootverbindingen (heen en weer dienst): Ios-Naxos, Ios-Serifos, Siros-Mikonos, Siros-Naxos en Siros-Ios.
   1. Geef de situatie weer in een graaf.
   2. Stel de bijbehorende verbindingsmatrix `C` op.
   3. Bereken `C + C^2`. Welke betekenis heeft deze matrix?
   4. Hoeveel bedraagt de graad van verbinding?
   5. Stel er komt een nieuwe bootverbinding tussen Serifos en Mikonos. Bereken dan de nieuwe graad van verbinding.


4. Een grootwinkelbedrijf brengt een goedkope Engelse fiets op de markt in vijf grote steden. Er zijn drie varianten: een herenfiets, een damesfiets en een kinderfiets. De herenfiets en de damesfiets kosten € 680,- per stuk, de kinderfiets kost € 420,- per stuk. De tabel laat zien welke aantallen fietsen het grootwinkelbedrijf bij de introductie van deze fiets heeft staan:
   
   

   		heren fiets	dames fiets	kinder fiets
   Amsterdam	40	40	60
   Rotterdam	30	30	30
   Groningen	20	20	40
   Zwolle	20	20	40
   Eindhoven	20	20	40

   
   
   1. Geef in een matrix weer welke verkoopwaarde deze beginvoorraden in de vijf steden hebben. Laat zien hoe je daarbij van matrixvermenigvuldiging gebruik kunt maken.
   Na drie maanden worden de fietsen die nog niet zijn verkocht geteld. Dat levert de volgende voorraad op:
   
   

   		heren fiets	dames fiets	kinder fiets
   Amsterdam	21	16	5
   Rotterdam	7	8	5
   Groningen	3	11	10
   Zwolle	8	6	0
   Eindhoven	3	9	7

   
   
   2. Stel een verkoopmatrix voor deze periode op waarin per fiets de aantallen verkochte exemplaren per vestiging staan.
   3. Welke type verkocht het best: de herenfiets, de damesfiets of de kinderfiets? In welke plaats werd elk type het best verkocht?
   4. De verkoopprijs van deze fietsen is ongeveer 40% hoger dan de inkoopprijs. Bereken per vestiging met behulp van matrixvermenigvuldiging hoeveel winst er is gemaakt op de verkoop van deze fietsen in de voorgaande drie maanden.
   5. De bedrijfsleiding wil zo spoedig mogelijk van de restvoorraad af. Deze restvoorraad wordt daarom in de aanbieding gedaan: elke fiets voor € 200,-. Bereken de totale winst die er op de Engelse fietsen wordt gemaakt.


5. Bij een populatie dieren zijn voor de verschillende leeftijdsklassen tellingen gedaan. De resultaten staan in de volgende tabel:
   
   

   leeftijd (jaren)	aantal dieren per 1-1-2000	aantal dieren per 1-1-2001	aantal nakomelingen per 100 exemplaren tussen 1-1-2000 en 1-1-2001
   0 –< 1	9600	13360	0
   1 –< 2	11500	7365	38
   2 –< 3	11200	9080	46
   3 –< 4	7800	7800	48
   4 –< 5	600	735	16

   
   
   Neem aan dat de geboortecijfers en de sterftecijfers ook gelden voor de volgende jaren.
   1. Stel een populatievoorspellingsmatrix op. Bereken de getallen in twee decimalen nauwkeurig.
   2. Bereken de verwachte populatie per 1-1-2001.
   3. Bereken de kans dat een pasgeboren dier van deze populatie ook echt 5 jaar oud wordt.
   4. Onderzoek het verloop van deze populatie dieren.

Toepassen

6. Nieuwe supermarkt

   In een zekere stad komt een nieuwe supermarkt C naast de bestaande A en B. Deze nieuwe supermarkt zal de bestaande gaan beconcurreren. De inwoners van deze stad zullen een nieuw kooppatroon gaan ontwikkelen. Lees hierover in:

   www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Matrices en grafen > Totaalbeeld > Toepassingen

   Bekijk vooral het opgestelde model voor de overgangen van de ้ne naar de andere supermarkt.
   1. Onderzoek door matrixvermenigvuldiging of een klant die als eerste bij supermarkt A winkelt volgens dit model een stabiel koopgedrag gaat vertonen.
   2. Hoeveel procent van de totale omzet van de supermarkten zal in deze plaats volgens dit model bij supermarkt A terecht komen?



7. Populatievoorspelling voor NL

   Ook voor de bevolking van Nederland kun je proberen een Leslie-matrix op te stellen. Door geboortecijfers of overlevingskansen aan te passen kun je verschillende scenario's doorrekenen voor de samenstelling van de toekomstige generaties. Ook kun je met migratie rekening houden. Zie hiertoe:

   www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Matrices en grafen > Totaalbeeld > Toepassingen

   Let eerst nog even niet op de factor migratie.
   1. In hoeveel generaties is de bevolking van Nederland in dit Excel-werkblad verdeeld?
   2. Stel een Lesliematrix op vanuit de geboortecijfers en de percentages overlevenden op dit werkblad.
   3. Voorspel hiermee de verdeling van de bevolking van Nederland in 2010. Waarom wijken de uitkomsten af van de gegevens op het werkblad?
   4. Waaraan kun je zien dat Nederland aan het "vergrijzen" is? Welke invloed heeft de migratie daarop?



8. Handelsreizigersprobleem

   Lees over het handelsreizigersprobleem in

   www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Matrices en grafen > Totaalbeeld > Toepassingen

   Schrijf er een korte verhandeling over. Ga daarbij ook in op de toepassingen.
   Zoek naar geschikte methoden om het probleem zo goed mogelijk "op te lossen". Verwerk daarin het volgende:
   • Zoek oplossingen voor het handelsreizigersprobleem voor een situatie met drie punten, met vier punten, met vijf punten, enzovoorts. Leg uit waarom veel wiskundigen dit probleem onoplosbaar achten.
   • Een voorbeeld van een methode om een verstandige route te vinden is de "naaste buur methode", waarbij je vanuit elk punt steeds naar het dichtsbijzijnde volgende punt gaat en zo de graaf doorloopt. Bepaal een route door 20 willekeurig gekozen punten met behulp van de "naaste buur methode" die vanuit ้้n punt weer in dat punt terecht komt. Laat zien dat in veel gevallen de "naastebuurmethode" niet de korste route oplevert.

Examenopgaven

9. Chaparral

   In de overgangszone tussen het woestijnklimaat en het gematigde klimaat aan de westkust van Noord-Amerika treft men over een oppervlakte van ongeveer 2000 km² een vegetatie aan van groenblijvende struiken. Men spreekt daar over de Chaparral. De brandbaarheid van de planten is sterk afhankelijk van de leeftijd. Vanwege het vele dorre materiaal zijn vooral de oudere planten zeer brandbaar. Brand heeft naast het gevaar voor mens en dier ook een belangrijke nuttige functie: op de plaats van de verbrande struiken komen vrijwel direct jonge en levenskrachtige planten uit de grond. Spontane branden worden daarom niet altijd geblust. De verjonging zorgt er immers voor dat er geen grote, uitgestrekte gebieden ontstaan van dor materiaal die bij brand tot catastrofes zouden kunnen leiden.
   Van deze situatie wordt een model gemaakt, waarbij men de volgende uitgangspunten hanteert:
   • De vegetatie wordt op grond van de leeftijd onderverdeeld in vier klassen:
     1. 0 –< 10 jaar;
     2. 10 –< 20 jaar;
     3. 20 –< 30 jaar;
     4. 30 jaar en ouder.
   • Als maat voor de omvang van een klasse neemt men niet het aantal planten maar de oppervlakte van het door die klasse bedekte gebied.
   • Per klasse blijft het percentage dat elke 10 jaar verbrandt, constant.
   • De totale oppervlakte van het gebied blijft 2000 km².
   Bij dit model past de volgende graaf:
   
   
   
   `b_i` is het gedeelte van klasse `i` dat verbrandt (`b_i < 1`) en `g_i` is het gedeelte van klasse `i` dat niet verbrandt (`g_i < 1`). Bij deze graaf kan een overgangsmatrix `M` worden opgesteld waarin `b_i` en `g_i` voorkomen. Het kental `m_(ij)` van deze matrix stelt daar bij de overgang van klasse `j` naar klasse `i` voor.
   1. Stel deze matrix `M` op.

   Oppervlakte in km2
   klasse		t = 0	t = 1
   1	302	462
   2	284	300
   3	314	278
   4	1100	960

   In de tabel staat vermeld hoe groot de oppervlakte is die elke klasse bedekt op het tijdstip `t = 0` en op het tijdstip `t = 1` (10 jaar later).
   2. Bereken `g_1`, `g_2`, `b_1` en `b_2` in drie decimalen nauwkeurig.
   Van de matrix `M` zijn met de computer de machten `M^2`, `M^3`, `M^4`, ... uitgerekend.
   Men constateerde dat de matrices `M^n` vanaf een zekere waarde van `n` nauwelijks meer verschillen. Zo zijn, na afronding op twee decimalen, de matrices `M^n` voor `n > 20` allemaal gelijk aan de volgende overgangsmatrix:

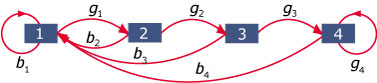
   `M^n ~~ ((0,19 , 0,19 , 0,19 , 0,19),(0,19 , 0,19 , 0,19 , 0,19),(0,18 , 0,18 , 0,18 , 0,18),(0,44 , 0,44 , 0,44 , 0,44))`

   Het blijkt dat op elke rij de getallen gelijk zijn.
   3. Welke conclusies kan men nu trekken voor de samenstelling van de Chaparralvegetatie?
   In de praktijk passen de beheerders van de Chaparral ook nog gecontroleerde bewuste afbranding van gedeeltes van de vegetatie ouder dan 10 jaar toe. In ons model nemen we ter vereenvoudiging aan dat dit direct na elke periode van 10 jaar in ้้n moment plaatsvindt. Neem aan dat men steeds 2,5% van klasse 2, 1,3% van klasse 3 en 7,2% van klasse 4 verbrandt.
   Dit proces van bewuste afbranding kan weergegeven worden door een 4×4-matrix `B`, waarin de hierboven genoemde percentages zijn verwerkt. Met behulp van het matrixproduct `B * M` kan dan het gezamenlijke proces over 10 jaar van de spontane afbranding, gevolgd door de gecontroleerde bewuste afbranding, beschreven worden.
   4. Stel matrix `B` op.

   (bron: examen vwo wiskunde A in 1994, eerste tijdvak, opgave 1)




10. IJs

    Een kleine ijsfabrikant levert de volgende vier producten:
    • vanille-ijs in literpakken;
    • duo-ijs in literpakken;
    • aardbeienijs in literpakken;
    • vanille-ijs in pakjes van 0,125 liter.
    Het duo-ijs bestaat voor 60% uit vanille-ijs en voor 40% uit aardbeienijs. De ijsfabrikant levert deze producten in dozen: in een doos gaan óf 16 literpakken van een zelfde product óf 80 kleine pakjes. Een winkelier bestelt 15 dozen met literpakken vanille-ijs, 10 dozen met duo-ijs, 4 dozen met aardbeienijs en 8 dozen met kleine pakjes vanille-ijs.
    1. Bereken hoeveel liter vanille-ijs en hoeveel liter aardbeienijs nodig is voor deze bestelling.
    De kosten die de ijsfabrikant maakt bestaan uit grondstofkosten, verpakkingskosten en transportkosten:
    • de grondstofkosten zijn € 2,80 per liter vanille-ijs en € 3,10 per liter aardbeienijs;
    • de verpakkingskosten zijn € 0,10 per pak of pakje en € 1,10 per doos;
    • de transportkosten zijn € 2,10 per doos.
    De prijzen die de ijsfabrikant rekent zijn: € 60,– voor een doos vanille-ijs, € 64,– voor een doos duo-ijs, € 70,– voor een doos aardbeienijs en € 80,– voor een doos met kleine pakjes vanille-ijs.
    2. Bereken de winst van de ijsfabrikant op de bestelling van de winkelier.
    Om te bepalen hoeveel liter vanille-ijs en hoeveel liter aardbeienijs hij nodig heeft voor een bestelling, maakt de ijsfabrikant gebruik van een computerprogramma. De benodigde hoeveelheden vanille-ijs (in liter) en aardbeienijs (in liter) worden door middel van de volgende matrixvermenigvuldiging berekend:

    `M * ((a),(b),(c),(d))`

    Hierbij geldt:
    `a` = het aantal dozen met literpakken vanille-ijs
    `b` = het aantal dozen met literpakken duo-ijs
    `c` = het aantal dozen met literpakken aardbeienijs
    `d` = het aantal dozen met kleine pakjes vanille-ijs
    3. Geef de matrix `M`. Licht je antwoord toe.
    Het computerprogramma kan ook de winst (`W`, in euro) op een bestelling berekenen. Het programma maakt gebruik van de volgende matrixformule:

    `W = ( A – B * M – C ) * ((a),(b),(c),(d))`

    Hierbij zijn `A`, `B` en `C`, evenals `M`, matrices die door de ijsfabrikant van de juiste elementen moeten worden voorzien. De matrices `A` en `C` moeten als volgt worden ingevuld: `A = `(60  64  70  80) en `C = `(4,8  4,8  4,8  11,2).
    4. Geef de matrix `B`. Licht je antwoord toe.

    (bron: examen vwo wiskunde A 1999, eerste tijdvak, aangepast aan euro)