Populatiematrices

Inleiding
Om voorspellingen te kunnen doen over de samenstelling van bepaalde populaties dieren maakte de Britse zoöloog P.H. Leslie in 1945 gebruik van grafen en matrices. Hoe dit werkt wordt hier beschreven in een model van een populatie kevers, het is zeer vergelijkbaar met het werken met overgangsmatrices.
Je leert nu:
- de samenstelling van populaties waarin generaties kunnen worden onderscheiden beschrijven met Leslie-matrices;
- het verloop van de samenstelling van zo'n populatie doorrekenen.
Je kunt al:
- rekenen met matrices, ook met je grafische rekenmachine;
- bij een graaf een matrix opstellen;
- werken met overgangsgrafen en overgangsmatrices.
Verkennen
Stel je een populatie van een bepaalde soort kevers voor die maximaal drie jaar oud worden. Uit statistisch onderzoek is gebleken:
- 20% van de kevers overleeft gemiddeld het eerste levensjaar;
- in het eerste levensjaar heeft een kever gemiddeld 0,8 nakomelingen;
- 4% van de kevers overleeft gemiddeld het tweede levensjaar;
- in het tweede levensjaar heeft een kever gemiddeld 2 nakomelingen;
- geen enkele kever wordt ouder dan drie jaar en in zijn derde jaar krijgt een kever geen nakomelingen.
Deze populatie kevers bestaat uit drie generaties. Er zijn 2000 nuljarige kevers, 600 éénjarige kevers en 80 tweejarige kevers geteld in een bepaald jaar.
> Hoe zal deze populatie zich de komende jaren ontwikkelen?
Uitleg
Stel je een populatie van een bepaalde soort kevers voor die maximaal drie jaar oud worden. Uit statistisch onderzoek is gebleken:
- 20% van de kevers overleeft gemiddeld het eerste levensjaar;
- in het eerste levensjaar heeft een kever gemiddeld 0,8 nakomelingen;
- 4% van de kevers overleeft gemiddeld het tweede levensjaar;
- in het tweede levensjaar heeft een kever gemiddeld 2 nakomelingen;
- geen enkele kever wordt ouder dan drie jaar en in zijn derde jaar krijgt een kever geen nakomelingen.
Deze populatie kevers bestaat uit drie generaties: nuljarige, éénjarige en twee jarige kevers.
Deze graaf beschrijft de overgangen tussen deze generaties. Daarbij is een overgangsmatrix op te stellen die Leslie-matrix wordt genoemd:
L =
Je ziet dat het "van ... naar ..." op dezelfde manier is gehanteerd dan bij overgangsmatrices gebruikelijk is. Daarom staan op de eerste rij van de matrix de geboortecijfers binnen de populatie. De overlevingskansen zijn de kentallen meteen onder de hoofddiagonaal. Heb je gegevens over de aantallen per generatie kun je nu gaan rekenen...
‡
Opgaven
-
Bekijk in de Uitleg hoe van de groei van een populatie kevers een model is gemaakt in de vorm van een Leslie-matrix.
- Is een Leslie-matrix een overgangsmatrix?
- Een Leslie-matrix wordt altijd zo geordend dat "van" boven staat en "naar" links vooraan. Waarom betekent dit dat de getallen op de eerste rij altijd geboortecijfers moeten zijn?
- Bekijk de Uitleg. Hoe groot is de kans dat een nuljarige kever zijn "eerste verjaardag" haalt?
- Hoe groot is de kans dat hij ook zijn "tweede verjaardag" haalt?
- Ga na of de populatie kevers naar een bepaalde evenwichtssituatie toe groeit.
Theorie
De Britse zoöloog P.H. Leslie ontwikkelde in 1945 een wiskundig model voor de ontwikkeling van een populatie planten of dieren. Daarbij verdeel je de populatie in gelijke leeftijdsintervallen die generaties heten. Vervolgens probeer je per generatie de overlevingskans en het gemiddelde geboortecijfer per element van de populatie vast te stellen (d.m.v. statistisch onderzoek).
Met deze gegevens kun je dan een populatievoorspellingsgraaf en een populatievoorspellingsmatrix opstellen.
Bij een populatie met vier generaties ziet dat er zo uit:
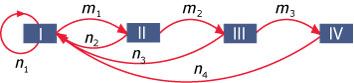
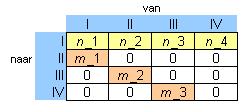
In de populatievoorspellingsmatrix of Leslie-matrix L vind je in de bovenste rij de geboortecijfers.
De overlevingskansen staan net onder de hoofddiagonaal.
Heb je nu de aantallen per generatie op een bepaald moment, dan kun je door matrixvermenigvuldiging berekenen hoe groot die aantallen precies één generatie later zijn. En als je door blijft vermenigvuldigen kun je voorspellen hoe de samenstelling van deze populatie zich zal ontwikkelen, of er sprake zal zijn van groei, of juist niet...
‡
Voorbeeld 1
Een bepaalde populatie zoogdieren kent vier generaties:
jonge dieren van 0 –< 2 jaar (generatie I), dieren van 2 –< 4 jaar (generatie II), dieren van 4 –< 6 jaar (generatie III) en oude dieren van 6 –< 8 jaar (generatie IV).
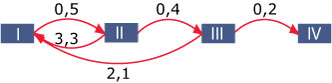
Deze populatiegraaf geeft het verloop van de samenstelling van de generaties weer.
Op 1-1-2000 waren er 590 jonge dieren, 360 dieren in generatie II, 200 dieren in generatie III en 80 oude dieren. Onderzoek hoe deze populatie zich zal ontwikkelen. Bereken ook het vervangingscijfer, dat is het verwachte aantal nakomelingen van één dier van deze populatie.
Antwoord
De Leslie-matrix L = , de populatiematrix is P2000 =
Dan is P2002 = L · P2000 en P2004 = L · P2002, enz.
Je ziet het aantal dieren sterk gaan toenemen.
Het vervangingscijfer is 0,5 · 3,3 + 0,5 · 0,4 · 2,1 ≈ 2,07. Geen wonder dat het aantal dieren groeit: elk dier zorgt gemiddeld voor 2,07 nakomelingen.
‡
| generatie | | 2000 | | 2002 | | 2004 |
|
| 0 –< 2 | 1150 |
1160 |
1880 |
| 2 –< 4 | 800 | 920 | 928 |
| 4 –< 6 | 120 | 320 | 368 |
| 6 –< 8 | 30 | 12 | 32 |
Voorbeeld 2
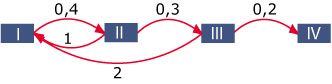
In de tabel zie je tellingen van een populatie zoogdieren die vier generaties kent. Alleen dieren van 2 –< 6 jaar krijgen jongen.
Beschrijf het verloop van de samenstelling van deze populatie dieren met een graaf en een Leslie-matrix.
Antwoord
De overlevingskansen per generatie vind je zo:
- van generatie 1 naar generatie 2: = = 0,8;
- van generatie 2 naar generatie 3: = = 0,4;
- van generatie 3 naar generatie 4: = = 0,1;
Alleen generaties 2 en 3 zorgen voor jongen, het gemiddelde in generatie 2 is a jongen per dier en in generatie 2 is dit b jongen per dier. Dan moet:
- 800a + 120b = 1160
- 920a + 320b = 1880
Je kunt dit oplossen door beide vergelijkingen in de vorm b = ... te schrijven en dan met je GR het snijpunt van beide lineaire functies te bepalen. Je vindt: a = 1 en b = 3.
Nu kun je de Leslie-matrix opstellen.
‡
Opgaven
-
Bestudeer het voorbeeld van de populatie dieren in Voorbeeld 1 nog eens goed.
- Welke tijdsduur heeft één generatie bij deze dieren?
- Hoe oud worden ze volgens de populatievoorspellingsgraaf maximaal?
- Welke getallen stellen de geboortecijfers of vruchtbaarheidscijfers voor?
- Hoe groot is de kans dat een pasgeborene van deze diersoort zes jaar oud wordt?
- Waarom kun je de kans dat een pasgeborene zeven jaar oud wordt niet vaststellen met deze gegevens?
- Wat is de betekenis van `L^2`? En van `L^3`?
- Bereken nu `P_(2002)` en `P_(2004)`. Laat zien dat deze populatie snel gaat groeien.
-
Een Leslie-matrix maak je vanuit een bepaald model voor de groei van een populatie.
Zo'n model ontstaat vanuit statistische gegevens over aantallen dieren of planten van opeenvolgende generaties.
In Voorbeeld 2 zie je hoe je een Leslie-matrix kunt opstellen vanuit dergelijke gegevens.
- Welke aannames doe je als je een Leslie-matrix gebruikt om de groei van een populatie te voorspellen?
- Bereken nu zelf de geboortecijfers.
- Stel een bijpassende Leslie-matrix L op.
- Onderzoek hoe deze populatie zoogdieren het gaat doen in de jaren na 2004.
- Bereken het vervangingscijfer.
-
Tweejarige planten bloeien pas in hun tweede levensjaar: na het dragen van
vruchten sterven de oude planten af. Per oude plant ontstaan er gemiddeld 8
jonge planten. Uit onderzoek blijkt dat 50% van de jonge planten éénjarige
planten worden en dat 25% van de éénjarige planten het tweede levensjaar
bereiken.
-
Geef dit weer in een graaf en stel een populatievoorspellingsmatrix voor deze tweejarige planten op.
-
Hoeveel kans heeft een jonge plant om zelf weer jonge planten voort te brengen?
-
Als er in een bepaald afgesloten gebied 400 jonge planten, 400 éénjarige planten en 100 oude planten worden waargenomen, hoe zal die populatie zich dan in de komende jaren ontwikkelen?
Geef de resultaten weer in grafieken.
Verwerken
 Een kudde antilopen bestaat uit dieren van vier generaties. De generatieduur is ongeveer 5 jaar.
Hun weidegebied is dichtbevolkt met roofdieren. Een bioloog heeft op basis van observaties een graaf opgesteld die de geboortecijfers en de overlevingskansen van de kudde antilopen weergeeft.
Stel je voor dat elke generatie in de kudde op zeker moment uit 100 dieren bestaat.
Een kudde antilopen bestaat uit dieren van vier generaties. De generatieduur is ongeveer 5 jaar.
Hun weidegebied is dichtbevolkt met roofdieren. Een bioloog heeft op basis van observaties een graaf opgesteld die de geboortecijfers en de overlevingskansen van de kudde antilopen weergeeft.
Stel je voor dat elke generatie in de kudde op zeker moment uit 100 dieren bestaat.
- Laat zien dat er geen sprake is van een natuurlijk evenwicht.
- Na hoeveel jaar is de kudde in dit model uitgestorven?
- Na 15 jaar wordt er besloten om het aantal roofdieren in het leefgebied van de kudde antilopen zodanig te verminderen dat hun overlevingskansen verdubbelen.
Onderzoek of het verdubbelen van de overlevingskansen het uitsterven van de kudde antilopen zal voorkomen.
- Na verdere observatie blijken ook de geboortecijfers van de kudde te worden beïnvloed door de afname van het aantal roofdieren. Geef daarvoor een verklaring.
- Stel dat de geboortecijfers zodanig veranderen dat alle dieren ouder dan 5 jaar gemiddeld voor 2 nakomelingen kunnen zorgen.
Onderzoek nu hoe het verloop van de aantallen dieren per generatie de komende jaren zal zijn.
Maak een passende grafiek voor het totaal aantal dieren in de loop der jaren. Is er sprake van exponentiële groei van de populatie? Zo ja, bepaal dan de groeifactor.
-
Van een ontwikkelingsland zijn de volgende bevolkingsgegevens bekend:
leeftijds
categorie | | 1900 | 1920 | 1940 | 1960 | 1980 |
|
| 0–<20 | 19,8 | 22,8 | 23,5 | 26,4 | 27,8 |
| 20–<40 | 8,9 | 8,9 | 10,2 | 10,6 | 11,9 |
| 40–<60 | 3,2 | 3,2 | 3,2 | 3,7 | 3,8 |
| 60–<80 | 0,3 | 0,4 | 0,4 | 0,4 | 0,5 |
| 80 en hoger | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
De aantallen in deze tabel zijn in miljoenen. Het gemiddeld aantal kinderen per hoofd van de bevolking is:
leeftijds
categorie | | kinderen |
| 0–<20 | 0,25 |
| 20–<40 |
1,97 |
| 40–<60 | 0,09 |
| 60–<80 | 0,00 |
- Bereken op grond van de eerste tabel de kansen dat iemand van een bepaalde leeftijdscategorie overgaat naar de volgende.
- Stel een Leslie-matrix op voor dit ontwikkelingsland.
- Waaraan kun je zien dat de sterfte onder kinderen in dit land hoog is?
- Voorspel de bevolkingssamenstelling van dit land in 2000 en 2020.
- De bevolking van dit land lijkt steeds sneller te groeien. Toon aan dat dit bij benadering exponentieel gebeurt in de periode van 1900 tot 2020.
- Bereken het jaar waarin de totale bevolking precies twee keer zo groot zal zijn dan in 1980 als je uitgaat van een zuiver exponentieel groeimodel.
-
Bij een uitgebreid onderzoek naar de groei van vogelpopulaties stelden Amerikaanse
biologen vast dat onder bepaalde omstandigheden de groei van een
populatie roodborstjes beschreven kan worden met een model dat in de graaf
hieronder is weergegeven.
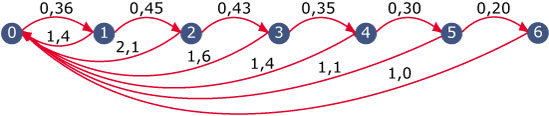
Uit deze graaf kan onder andere worden afgelezen dat 45% van de éénjarige
roodborstjes de tweejarige leeftijd bereikt en dat 100 éénjarige vogels per jaar
gemiddeld 140 jongen voortbrengen. Ook blijkt uit de graaf dat de vogels de
leeftijd van zeven jaar niet bereiken.
- Stel een bijpassende populatievoorspellingsmatrix op.
Een populatie waarvoor de voorgaande gegevens gelden, bestond op 1 juli 1990
(tijdstip `t = 0`) uit 2022 roodborstjes. De tabel geeft de verdeling over de verschillende
leeftijden weer.
| leeftijd | | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|
| roodborstjes | 1250 | 440 | 200 | 80 | 30 | 20 | 2 |
- Onderzoek of het totale aantal roodborstjes op 1 juli 1991 (`t = 1`) volgens dit model minder dan 1% afwijkt van het totale aantal op 1 juli 1990.
- Onder het vervangingscijfer versta je de verwachtingswaarde van het aantal jongen dat een roodborstje gedurende het hele leven krijgt.
Hoe groot zou dit vervangingscijfer zijn als geen enkel roodborstje de tweejarige leeftijd zou bereiken?
- Toon aan dat het vervangingscijfer in het door de graaf beschreven model ongeveer gelijk is aan 1.
Uit voortgezet onderzoek bleek dat de in de graaf vermelde overlevingskansen
onafhankelijk zijn van de populatieomvang, maar dat de in de graaf vermelde
vruchtbaarheidscijfers slechts gelden voor een populatie die in totaal ongeveer
2000 roodborstjes telt. Op grond van hun tellingen veronderstelden de onderzoekers
dat het model als volgt bijgesteld moest worden: voor de overgang van
tijdstip `t` naar tijdstip `t + 1` moeten alle vruchtbaarheidscijfers uit de graaf vermenigvuldigd
worden met een factor `k` die afhangt van de populatieomvang `N_t` op tijdstip `t`:
`k = 2 - (N_t)/2000`
- Bereken voor welke populatieomvang deze bijstelling leidt tot een halvering van de vruchtbaarheidscijfers in vergelijking met die van het oorspronkelijke model.
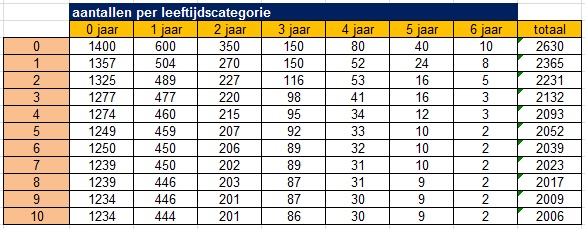
- De volgende tabel is verkregen door een computer volgens het bijgesteld model de aantallen op de tijdstippen `t = 1, 2, ... , 10` te laten berekenen.
Bereken hoeveel jongen de groep van 1400 nuljarigen van tijdstip `t = 0` volgens het bijgestelde model in hun derde levensjaar zal voortbrengen.
Neem totaal 2022 en ga uit van de situatie in 1990.
Testen
-
Een bepaalde diersoort wordt in drie leeftijdsgroepen van 4 jaren verdeeld. Op
zeker tijdstip (`t = 0`) is de opbouw van een populatie van deze dieren:
- 200 jonge dieren;
- 100 volwassen dieren;
- 50 oude dieren.
Er worden geen dieren ouder dan 12 jaar. Deze graaf beschrijft het verloop tussen
de leeftijdscategorieën van deze diersoort:
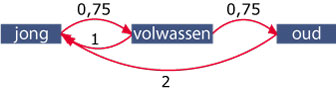
- Stel een populatievoorspellingsmatrix `P` voor deze diersoort op.
- Wat is de betekenis van `P^2`? En van `P^3`?
- Bereken de aantallen dieren per leeftijdsgroep over 4 jaar (`t = 1`).
- Onderzoek de groei van deze populatie dieren en teken een grafiek van het verloop van de totale populatie.
- Is er sprake van exponentiële groei? Zo ja, bepaal dan de groeifactor.
- Hoeveel bedraagt de levensverwachting van een pasgeboren exemplaar van deze diersoort?
Door vervuiling van hun natuurlijk milieu worden de overlevingskansen van deze populatie dieren na 8 jaar (`t = 2`) kleiner.
Stel dat alle overlevingskansen met dezelfde factor `k` worden vermenigvuldigd.
- Bereken bij welke waarde van `k` de populatie nog net niet zal gaan uitsterven.








 Een kudde antilopen bestaat uit dieren van vier generaties. De generatieduur is ongeveer 5 jaar.
Hun weidegebied is dichtbevolkt met roofdieren. Een bioloog heeft op basis van observaties een graaf opgesteld die de geboortecijfers en de overlevingskansen van de kudde antilopen weergeeft.
Stel je voor dat elke generatie in de kudde op zeker moment uit 100 dieren bestaat.
Een kudde antilopen bestaat uit dieren van vier generaties. De generatieduur is ongeveer 5 jaar.
Hun weidegebied is dichtbevolkt met roofdieren. Een bioloog heeft op basis van observaties een graaf opgesteld die de geboortecijfers en de overlevingskansen van de kudde antilopen weergeeft.
Stel je voor dat elke generatie in de kudde op zeker moment uit 100 dieren bestaat.


