
Overgangen

Inleiding
Bij verstedelijking is er sprake van een overgang van mensen vanaf het platteland naar stedelijke gebieden. Dit kan op twee manieren: het platteland raakt ontvolkt omdat mensen naar de steden trekken en/of steeds meer platteland wordt bebouwd en verandert zo in stedelijk gebied. Het effect is in beide gevallen dat steeds meer mensen in "de stad" wonen en steeds minder op het platteland...
Je leert nu:
- overgangen beschrijven m.b.v. gerichte matrices;
- werken met luswegen;
- een overgangsmatrix opstellen;
- narekenen of er sprake zal zijn van stabilisatie of niet, werken met Markov-ketens.
Je kunt al:
- rekenen met matrices, ook met je grafische rekenmachine;
- bij een graaf een matrix opstellen.
Verkennen
In een bepaalde regio verhuist jaarlijks een deel van de bevolking in de stedelijke gebieden naar het platteland en omgekeerd. Ook zijn er uiteraard verhuizingen van en naar buiten deze regio, maar die percentages zijn te verwaarlozen. Jaarlijks verhuist 29,9% van de bevolking van het platteland naar de stad en 9,8% van de stedelijke bevolking naar het platteland.
Op dit moment wonen er in deze regio 560.000 mensen in de stedelijke gebieden en 1.224.000 op het platteland.
> Hoe zal dat over 20 jaar zijn als deze ontwikkeling zo doorgaat?
Uitleg
Het volgende wiskundige model beschrijft de migratie in een bepaald gebied:
- Jaarlijks verhuist 20% van de mensen die in stedelijke gebieden wonen naar het platteland.
- Jaarlijks verhuist 30% van de mensen die op het platteland wonen wonen naar een stedelijke omgeving.
- De migratie van en naar buiten dit gebied is te verwaarlozen.
Dit model kun je beschrijven met de getekende migratiegraaf.
Dit is een gerichte graaf met luswegen. Dat komt omdat behalve de mensen die van S (stedelijk gebied) naar P (platteland gaan en omgekeerd, er ook mensen zijn die in S dan wel P blijven wonen.
Bij een migratiegraaf past een migratiematrix M.
In de tabel zie je hoe daarbij het "van ... naar ..." is geregeld. Die keuze bepaald hoe je met matrixvermenigvuldiging de verdeling van de bevolking over stedelijke gebied en platteland voor komende jaren berekent. Stel je voor dat in het jaar 2000 in dit gebied 84.000 mensen in de stad en 12.000 mensen op het platteland wonen. Dan bereken je zo deze aantallen voor 2001:
B2001 = M · B2000 =
En de aantallen voor 2002 zijn B2002 = M · B2001, enzovoorts.
‡
Opgaven
-
Bekijk in de Uitleg hoe van de migratie in een bepaald gebied een graaf is gemaakt.
- Waarom werk je bij het in beeld brengen van de overgangen met een gerichte graaf?
- De in het voorbeeld getekende migratiegraaf bevat twee zogenaamde luswegen. Welke? Waarom kom je bij een overgangsgraaf bijna altijd luswegen tegen?
- Waarom is in de migratiematrix de som van de kentallen in een kolom altijd 1?
- Waarom hoeft dat voor de som van de kentallen in een rij niet zo te zijn?
- Je ziet dat in het migratieschema en dus ook de migratiematrix "van" bovenaan staat en "naar" links vooraan.
Wat betekent dit voor de bevolkingsmatrix B2000? Moet elke overgangsmatrix op deze manier worden samengesteld?
- Bepaal met behulp van je grafische rekenmachine het aantal inwoners op het platteland in 2005.
Theorie
De overgangen tussen verschillende situaties A, B en C in een vaste tijdsperiode kunnen worden beschreven met een overgangsgraaf.
Dit is een gerichte graaf met luswegen. Dat komt omdat er behalve van overgang van de éne situatie naar de andere ook sprake is van in dezelfde situatie blijven. De getallen bij de pijlen zijn overgangskansen die daarom alleen waarden van 0 t/m 1 kunnen aannemen. Het totaal van de overgangskansen vanuit één bepaalde situatie is altijd 1.
Bij een overgangsgraaf past een overgangsmatrix M.
In de tabel zie je hoe daarbij het "van ... naar ..." is geregeld. Die keuze bepaalt hoe je met matrixvermenigvuldiging de verdeling over de verschillende situaties telkens één periode verder berekent. Dit betekent bovendien dat de som van de kentallen in elke kolom 1 is.
Als de 3×1-matrix V0 de verdeling van de aantallen over de drie situaties voorstelt, dan zijn de aantallen na één periode V1 = M · V0, na twee periodes V2 = M · V1, enzovoorts. (Je moet wel denken om een passende en steeds gelijke volgorde van aantallen en kansen bij de verschillende situaties.)
Blijf je zo doorrekenen, dan vormen de verdelingen een zogenaamde Markov-keten.
Soms leidt dit doorrekenen tot een evenwichtssituatie, waarin de aantallen voor A, B en C niet meer veranderen.
‡
Voorbeeld 1
Het volgende wiskundige model beschrijft de migratie in een bepaald gebied:
- Jaarlijks verhuist 20% van de mensen die in stedelijke gebieden wonen naar het platteland.
- Jaarlijks verhuist 30% van de mensen die op het platteland wonen wonen naar een stedelijke omgeving.
- De migratie van en naar buiten dit gebied is te verwaarlozen.
Bij de migratiegraaf past deze migratiematrix M. In het jaar 2000 wonen in dit gebied 84.000 mensen in de stad en 12.000 mensen op het platteland.
Hoeveel zijn dat er in 2020?
Antwoord
B2001 = M · B2000 = M ·
en B2002 = M · B2001 = M · enzovoorts...
Sneller is: B2020 = M20 · B2000 = M20 · ≈
Van verstedelijking is in dit geval geen enkele sprake...
‡
Voorbeeld 2
Bekijk de migratie in Voorbeeld 1 nog eens.
Onderzoek of de verdeling van het aantal mensen in stedelijke gebieden en het aantal mensen op het platteland naar een evenwichtssituatie toegroeit op den duur.
Antwoord
Dat is het geval als er een matrix bestaat zo, dat = M · .
Met de gegeven matrix M betekent dit: 0,8a + 0,3b = a en 0,2a + 0,7b = b. Uit elk van deze twee vergelijkingen volgt: 0,2a = 0,3b ofwel a = 1,5b.
Omdat a + b = 84.000 + 12.000 = 96.000 is 2,5b = 96.000 en dus b = 38.400. Dan is a = 96.000 – 38.400 = 57.600. Kennelijk ontstaat er op den duur een evenwichtssituatie.
‡
Voorbeeld 3
De meeste mensen hebben hun auto verzekerd tegen schade. Bijna alle autoschadeverzekeringen kennen het principe van de 'no-claim-korting'. Dat gaat bij een bepaalde verzekeringsmaatschappij (sterk vereenvoudigd) op deze manier:
- als je een bepaald jaar geen schade claimt, krijg je het volgende jaar een korting van 20% op de jaarpremie van € 800,00;
- je kunt maximaal 60% van de jaarpremie aan premiekorting krijgen;
- als je wel schade claimt in een jaar, betaal je het volgende jaar weer de volle jaarpremie
Ga er van uit dat ongeveer 30% van alle verzekerden jaarlijks een schade claimt.
Hoeveel premie ontvangt de maatschappij op de lange duur gemiddeld per klant?

Antwoord
De bijbehorende overgangsmatrix is:
M =
Al snel ontstaat er een evenwichtssituatie als je de 4×1-premiematrix P met M blijft doorvermenigvuldigen. De gemiddelde premie per klant wordt dan € 560,00.
‡
Opgaven
-
Bestudeer het voorbeeld van de migratie in Voorbeeld 1 nog eens goed.
- Laat zien, dat je door doorrekenen met de gegeven matrix de evenwichtssituatie krijgt die in het voorbeeld wordt gegeven.
- Wanneer de evenwichtssituatie ontstaat hangt af van het aantal decimalen dat belangrijk is. Licht dit toe.
- Waarom is een berekening zoals in Voorbeeld 2 nodig om echt zeker te weten dat er evenwicht ontstaat?
- Voer die berekening zelf nog eens uit.
-
Een supermarkt verkoopt twee merken waspoeder, Bright en Shine. Er wordt een derde merk geïntroduceerd, met de naam White. Dit nieuwe merk zou op den
duur één van beide andere merken moeten vervangen. De bedrijfsleiding is dan ook erg geïnteresseerd in het koopgedrag van de consument. Er wordt aan 120
klanten die al hun waspoeder kopen bij deze supermarkt gevraagd naar hun koopgedrag. Daarbij blijkt dat ze gemiddeld een maand doen met een groot pak
waspoeder van een bepaald merk en dan aan het einde van die maand een nieuw pak aanschaffen.
De volgende tabel geeft de wisseling van merken weer:
| | Volgende maand | |
| W | S | B | totaal |
|
Deze
maand | W | 15 | 3 | 2 | 20 |
| S | 10 | 25 | 15 | 50 |
| B | 15 | 15 | 20 | 50 |
| totaal | 40 | 43 | 37 | 120 |
- Hoeveel van deze klanten hebben in beide maanden waspoeder van het merk Shine gekocht?
- Hoeveel procent van de klanten is van merk gewisseld?
- Stel voor de overgangen van het éne merk naar het andere een graaf en een overgangsmatrix W op.
- Welke overgangsperiode kent de graaf?
De bedrijfsleiding gaat ervan uit dat deze overgangen voor de komende maanden blijven gelden.
- Stel je nu voor dat aanvankelijk de verdeling voor de merken Bright en Shine als volgt was: 35% van de klanten koopt Bright en 65% van de klanten koopt Shine.
Bereken dan de verdeling van de klanten over de drie verschillende merken na de introductie van het merk White.
- Bereken ook de verdeling van de klanten over de drie verschillende merken een maand later.
- Onderzoek of er een evenwichtssituatie ontstaat en bereken de verdeling van de klanten over de drie merken waspoeder in de evenwichtssituatie.
- Kan het nieuwewaspoeder inderdaad één van beide andere merken vervangen?
-
In Voorbeeld 3 zie je hoe een no-claim-korting werkt.
-
Waar vind je in de graaf de korting als je geen schade claimt van 20% op de jaarpremie terug?
-
Iemand heeft twee jaar schadevrij gereden, maar in zijn derde jaar krijgt hij schade aan zijn auto.
Als hij deze schade van € 1000,- claimt bij de verzekering, hoeveel premie moet hij dan een jaar later betalen? Onderzoek of het voor hem verstandig is deze schade te claimen.
-
Hoe groot is de kans dat iemand in zijn vierde jaar de volle premie moet betalen?
-
Bekijk de overgangsmatrix in Voorbeeld 3. Welke betekenis hebben M2 en M3?
-
Onderzoek nu zelf of er een evenwichtssituatie ontstaat.
Verwerken
 Wanneer een bepaald dier in een nieuw leefgebied terechtkomt, dan moet het zich
aanpassen aan de omstandigheden. Er zijn plaatsen waar zo’n dier kan drinken en
plaatsen waar het zijn voedsel vindt. Gedurende de dag zwerft het voortdurend
tussen die plaatsen heen en weer, waarbij langzamerhand een vast patroon gaat
ontstaan. De nachten blijven buiten beschouwing, omdat het dier dan niet actief is.
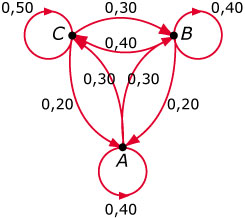
Stel dat er één drinkplaats D is en twee plaatsen
om voedsel te halen, A en B. Een bioloog noteert
steeds om het uur waar hij het dier aantreft, bij
D, bij A of bij B. Op grond daarvan maakt hij de
de graaf die je hiernaast ziet.
Wanneer een bepaald dier in een nieuw leefgebied terechtkomt, dan moet het zich
aanpassen aan de omstandigheden. Er zijn plaatsen waar zo’n dier kan drinken en
plaatsen waar het zijn voedsel vindt. Gedurende de dag zwerft het voortdurend
tussen die plaatsen heen en weer, waarbij langzamerhand een vast patroon gaat
ontstaan. De nachten blijven buiten beschouwing, omdat het dier dan niet actief is.
Stel dat er één drinkplaats D is en twee plaatsen
om voedsel te halen, A en B. Een bioloog noteert
steeds om het uur waar hij het dier aantreft, bij
D, bij A of bij B. Op grond daarvan maakt hij de
de graaf die je hiernaast ziet.
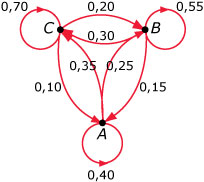
- Maak bij deze graaf een overgangsmatrix `M`.
- Op zeker moment is het dier aan het drinken. Geef dit weer in een kolommatrix `P_0`.
- Bereken `P_1 = M * P_0`. Welke betekenis heeft de matrix `P_1`?
- Bereken op dezelfde wijze de matrix `P_2`.
- Vanaf welke waarde van `n` geldt: `M· P_n = P_n`?
- Hoeveel procent van zijn actieve tijd brengt het dier op den duur op elk van de plaatsen `D`, `A` en `B` door?
-
De aanleg tot het hebben van overgewicht blijkt van ouders op kinderen teworden
overgedragen. Een onderzoeker heeft alle mensen in drie klassen verdeeld:
- mensen met overgewicht op hun 40ste;
- mensen met normaal gewicht op hun 40ste;
- mensen met ondergewicht op hun 40ste.
Op grond van onderzoek heeft zij het gewicht van ouders op hun 40ste vergeleken
met dat van hun kinderen op hun 40ste en de volgende tabel gemaakt:
| | | kinderen |
| | A | B | C |
|
| ouders | A | 70 | 20 | 10 |
| B | 30 | 50 | 20 |
| C | 15 | 60 | 25 |
- Hoe kun je aan de tabel zelf zien dat het hier waarschijnlijk een tabel met percentages betreft?
- Teken een overgangsgraaf en stel de bijbehorende overgangsmatrix op.
In een bepaalde regio wordt bij een bevolkingsonderzoek geconstateerd dat de
verdeling van de ouders over de drie categorieën er als volgt uitziet:
- klasse A: 1400 personen;
- klasse B: 2600 personen;
- klasse C: 800 personen.
- Hoe ziet de verdeling van hun kinderen over deze categorieën er een generatie later uit als de overgangsmatrix een geschikt model is voor de overdracht van overgewicht?
- De aantallen per categorie zullen in de loop van de generaties gaan veranderen.
Je kunt daar grafieken bij maken, ervan uitgaande dat het aantal personen per generatie niet verandert. Maak een grafiek voor elk van de categorieën.
- Zal er op den duur een evenwichtssituatie ontstaan? Zo ja, bereken dan de aantallen per categorie.
-
Een autoverhuurbedrijf heeft in Nederland vele vestigingen. Gehuurde auto’s
mogen op een andere vestiging worden teruggebracht. De bedrijfsleiding houdt
bij hoe het verloop van de auto’s over de verschillende vestigingen is. Daarbij
spelen matrices een rol.
In een model van deze situatie ga je bijvoorbeeld uit van drie vestigingen A, B en
C. Stel dat voor de verschillende vestigingen per dag geldt:
- vestiging A: 10% van de aanwezige auto’s wordt in B ingeleverd, 30% gaat naar C;
- vestiging B: 10% van de aanwezige auto’s wordt in A ingeleverd, 10% gaat naar C;
- vestiging C: 10% van de aanwezige auto’s wordt in A ingeleverd, 20% gaat naar B.
- Teken voor dit model een graaf en stel een bijpassende overgangsmatrix `A` op.
- Ga uit van een beginsituatie van 200 auto’s per vestiging.
Onderzoek of er na verloop van tijd een evenwichtssituatie ontstaat en bereken voor de evenwichtssituatie het aantal auto’s dat er per vestiging.
- Bereken `A^2`. Welke betekenis heeft deze matrix?
- Bereken `A^3, A^4, A^5, ...` en rond (achteraf!) de kentallen van deze matrices af op twee decimalen nauwkeurig. Wat zie je op den duur gebeuren met de machten van matrix `A`?
- Is het ontstaan van evenwicht afhankelijk van de beginsituatie? Licht je antwoord toe.
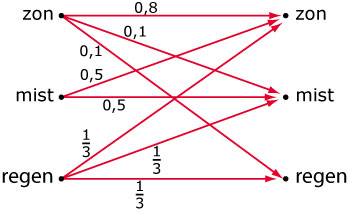 De weerman uit Santa Barbara in de Verenigde Staten onderscheidt in het voorjaar drie soorten
dagen: zonnige dagen, mistige dagen en regenachtige dagen. Hij heeft uit onderzoek afgeleid
dat er verband bestaat tussen het weer op twee opeenvolgende dagen. Het schema hiernaast met
overgangskansen geeft dat weer.
De weerman uit Santa Barbara in de Verenigde Staten onderscheidt in het voorjaar drie soorten
dagen: zonnige dagen, mistige dagen en regenachtige dagen. Hij heeft uit onderzoek afgeleid
dat er verband bestaat tussen het weer op twee opeenvolgende dagen. Het schema hiernaast met
overgangskansen geeft dat weer.
- Teken een graaf waarin alleen de drie knooppunten `Z` voor zonnige dag, `M` voor mistige dag en `R` voor regenachtige dag voorkomen en waarin alle overgangskansen staan beschreven.
- Stel de bijpassende overgangsmatrix `W` op.
- Het is maandag zonnig in Santa Barbara. Hoe groot is de kans dat het woensdag weer zonnig is?
- Bereken `W^2`. Wat stelt deze matrix voor?
- Hoe groot is de kans dat het dinsdag én woensdag zonnig is?
- Hoe groot is de kans dat het minstens één van deze beide dagen zonnig is?
Testen
 Toen de smartphone werd geïntroduceerd groeide het aantal jongeren dat in het
bezit is van zo’n apparaat snel. Op een scholengemeenschap van 1500 leerlingen
hebben leerlingen in 2010 het toenemend bezit van de smartphone onderzocht.
Toen de smartphone werd geïntroduceerd groeide het aantal jongeren dat in het
bezit is van zo’n apparaat snel. Op een scholengemeenschap van 1500 leerlingen
hebben leerlingen in 2010 het toenemend bezit van de smartphone onderzocht.
- Bij de start van het onderzoek bleek 15% van de leerlingen een smartphone te hebben.
- Van het aantal leerlingen dat geen smartphone had, bleek een maand later 4% er wel één te hebben.
- Van het aantal leerlingen dat wel een smartphone had, bleek een maand later 1% geen smartphone meer te hebben.
- Maak hierbij een graaf en een overgangsmatrix `S`.
- Hoeveel leerlingen hebben één maand na de start van het onderzoek een smartphone?
- Bepaal `S^2` en leg uit welke betekenis deze matrix heeft.
Ga ervan uit dat de overgangsmatrix `S` ook nog na het onderzoek beschrijft hoe
het aantal smartphonebezitters in de loop van een maand verandert.
- Hoeveel procent van de leerlingen heeft na een half jaar een smartphone?
- Na verloop van tijd ontstaat er een evenwichtssituatie als het aantal leerlingen van de school niet verandert.
Hoeveel leerlingen hebben er in die evenwichtssituatie nog geen smartphone?
-
Een bepaald medicijn wordt gefabriceerd in een reactievat. De kwaliteit van het
medicijn is bij de fabricage moeilijk onder controle te houden. Als er een kleinigheid
misgaat in het reactievat is de gefabriceerde partij onbruikbaar. Hoewel het
reactievat na elke onbruikbare partij grondig wordt gereinigd, kunnen minieme
achtergebleven resten van invloed zijn op de fabricage van de volgende partij.
Voor het fabricageproces gelden de volgende kansen:
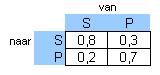
| | | partij is |
| | onbruikbaar | bruikbaar |
|
volgende
partij is | onbruikbaar | 0,4 | 0,2 |
| bruikbaar | 0,6 | 0,8 |
- Een bepaalde partij is bruikbaar. Hoe groot is de kans dat precies één van de eerstvolgende twee partijen onbruikbaar is?
- `M` is de overgangsmatrix die de kansen beschrijft op de bruikbaarheid of onbruikbaarheid van de volgende partij. Wat stelt de matrix `M^n` dan voor?
- Bij toenemende waarden van `n` nadert de matrix `M^n` een bepaalde evenwichtssituatie. Hoeveel procent bruikbare partijen zullen er op den duur worden gefabriceerd?









 Wanneer een bepaald dier in een nieuw leefgebied terechtkomt, dan moet het zich
aanpassen aan de omstandigheden. Er zijn plaatsen waar zo’n dier kan drinken en
plaatsen waar het zijn voedsel vindt. Gedurende de dag zwerft het voortdurend
tussen die plaatsen heen en weer, waarbij langzamerhand een vast patroon gaat
ontstaan. De nachten blijven buiten beschouwing, omdat het dier dan niet actief is.
Stel dat er één drinkplaats D is en twee plaatsen
om voedsel te halen, A en B. Een bioloog noteert
steeds om het uur waar hij het dier aantreft, bij
D, bij A of bij B. Op grond daarvan maakt hij de
de graaf die je hiernaast ziet.
Wanneer een bepaald dier in een nieuw leefgebied terechtkomt, dan moet het zich
aanpassen aan de omstandigheden. Er zijn plaatsen waar zo’n dier kan drinken en
plaatsen waar het zijn voedsel vindt. Gedurende de dag zwerft het voortdurend
tussen die plaatsen heen en weer, waarbij langzamerhand een vast patroon gaat
ontstaan. De nachten blijven buiten beschouwing, omdat het dier dan niet actief is.
Stel dat er één drinkplaats D is en twee plaatsen
om voedsel te halen, A en B. Een bioloog noteert
steeds om het uur waar hij het dier aantreft, bij
D, bij A of bij B. Op grond daarvan maakt hij de
de graaf die je hiernaast ziet.
 De weerman uit Santa Barbara in de Verenigde Staten onderscheidt in het voorjaar drie soorten
dagen: zonnige dagen, mistige dagen en regenachtige dagen. Hij heeft uit onderzoek afgeleid
dat er verband bestaat tussen het weer op twee opeenvolgende dagen. Het schema hiernaast met
overgangskansen geeft dat weer.
De weerman uit Santa Barbara in de Verenigde Staten onderscheidt in het voorjaar drie soorten
dagen: zonnige dagen, mistige dagen en regenachtige dagen. Hij heeft uit onderzoek afgeleid
dat er verband bestaat tussen het weer op twee opeenvolgende dagen. Het schema hiernaast met
overgangskansen geeft dat weer.
 Toen de smartphone werd geïntroduceerd groeide het aantal jongeren dat in het
bezit is van zo’n apparaat snel. Op een scholengemeenschap van 1500 leerlingen
hebben leerlingen in 2010 het toenemend bezit van de smartphone onderzocht.
Toen de smartphone werd geïntroduceerd groeide het aantal jongeren dat in het
bezit is van zo’n apparaat snel. Op een scholengemeenschap van 1500 leerlingen
hebben leerlingen in 2010 het toenemend bezit van de smartphone onderzocht.