Grafen

Inleiding

Je hebt leren werken met matrices. Maar tot nu toe was dat weinig nuttig, voorraadberekeningen kun je ook wel zonder matrixrekening. Werken met matrices is vooral nuttig in combinatie met grafen.
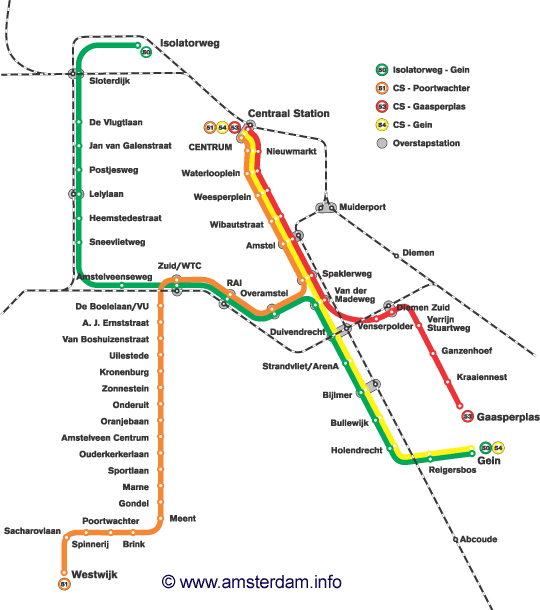
Het metronetwerk van Amsterdam is een voorbeeld van zo'n graaf met knooppunten (de stations) en verbindingen (de spoorlijnen).

Je leert nu:

• het begrip graaf met knooppunten en verbindingen;
• gelijke grafen herkennen;
• het verschil tussen directe wegen en verbindingen, gerichte en ongerichte grafen;
• de verbindingsmatrix maken en gebruiken en de graad van verbinding van een graaf berekenen.

Je kunt al:

• rekenen met matrices;
• matrices in je grafische rekenmachine invoeren.

Verkennen

Het metronetwerk van Amsterdam is een graaf met knooppunten (de stations) en verbindingen (de spoorlijnen). Bekijk alleen de stations Centraal, Zuid/WTC, Isolatorweg, Westwijk, Gein en Gaasperplas. Stel je voor dat er geen andere stations zijn.

> Maak een nieuwe graaf met alleen deze stations als knooppunten. Trek tussen twee punten een verbindingslijn als er een rechtstreekse verbinding tussen bestaat (dus zonder overstappen).
> Hoe kun je dit in een matrix C weergeven? En wat heb je dan aan die matrix?

Uitleg

Het metronetwerk van Amsterdam is een graaf met knooppunten (de stations) en verbindingen (de spoorlijnen). Bekijk alleen de stations Centraal, Zuid/WTC, Isolatorweg, Westwijk, Gein en Gaasperplas. Stel je voor dat er geen andere stations zijn. Je kunt dan deze graaf maken. De genoemde stations zijn de knooppunten van de graaf en de verbindingslijnen geven aan of er een rechtstreekse (zonder overstappen) verbinding tussen twee stations is.

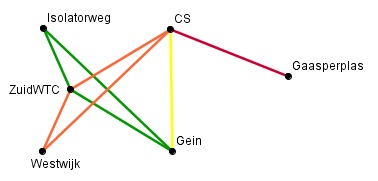
Deze graaf geeft de metroverbindingen tussen de stations Centraal, Zuid/WTC, Isolatorweg, Westwijk, Gein en Gaasperplas weer. Er staan geen getallen bij, een verbindingslijn betekent een rechtstreekse (zonder overstappen) verbinding tussen twee stations.
Je kunt de knooppunten rustig verplaatsen en de verbindingen mogen ook best kromme lijnen zijn, de graaf verandert niet.

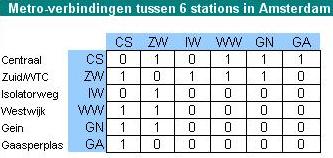
Je kunt bij deze graaf een verbindingsmatrix C opstellen. In C vind je het aantal éénstapsverbindingen tussen twee punten, in C² het aantal tweestapsverbindingen (verbindingen met één overstap) tussen twee punten, enz.
Een verbindingsmatrix is altijd vierkant en symmetrisch t.o.v. de hoofddiagonaal want elke verbinding werkt in beide richtingen.

De graad van verbinding van een verbindingsgraaf is het aantal bestaande verbindingen (hier 8) gedeeld door het totaal aantal mogelijke verbindingen (hier 6 · 5 / 2 = 15).

‡

Opgaven

1. Bekijk in de Uitleg hoe van de metroverbindingen tussen 6 stations in Amsterdam een graaf is gemaakt.
   1. Stel zelf de bijbehorende verbindingsmatrix `C` op .
   2. Bereken de graad van verbinding van deze graaf.
   3. Tussen welke waarden kan de graad van verbinding van een graaf liggen? Wanneer is er sprake van een hoge "dichtheid" van de verbindigen?
   4. Bereken `C^2`. Leg uit waarom deze matrix alle zogenaamde tweestapsverbindingen in de graaf weergeeft.
   5. Schrijf alle tweestapsverbindingen vanuit het Centraal Station op.
   6. Welke betekenis heeft de matrix `C + C^2`? Waarom komen er in deze matrix nog nullen voor?
   7. Welke driestapsverbindingen zijn er vanuit het Centraal Station mogelijk?
   8. Komen er in de matrix `C + C^2 + C^3` ook nog nullen voor? Waarom?


2. Onder de "diameter" van een graaf versta je het maximale aantal stappen dat nodig is om vanuit een willekeurig knooppunt in een willekeurig ander knooppunt te komen.
   1. Hoe groot is de diameter van de graaf van de vorige opgave?
   2. Van twee plaatsen die net zoveel stappen van elkaar verwijderd liggen als de diameter van de graaf bedraagt, zeg je dat ze diametraal liggen. Noem alle plaatsen die diametraal liggen.

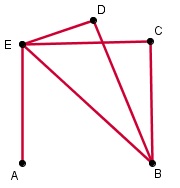
Theorie

Je ziet hier een graaf met 5 knooppunten en 6 verbindingslijnen.
De lengte en de vorm van de verbindingslijnen en de plaats van de knooppunten zijn niet van belang. Twee grafen zijn namelijk gelijk als ze hetzelfde aantal knooppunten en dezelfde onderlinge verbindingen hebben.

Een verbindingsgraaf zoals deze is een ongerichte graaf, want elke verbinding werkt in beide richtingen. De bijbehorende verbindingsmatrix is vierkant en symmetrisch t.o.v. de hoofddiagonaal, elk kental is 0 (geen verbinding) of 1 (wel een verbinding). (Bij meerdere verbindingen tussen twee punten wordt het kental toch 1 omdat het alleen gaat om wel of geen rechtstreekse verbinding zonder tussenstation.) De graad van verbinding is het aantal bestaande verbindingen gedeeld door het totaal aantal mogelijke verbindingen.

Je kunt bij een dergelijke graaf ook de afstanden bij de verbindingen zetten, dan krijg je een afstandengraaf met een bijbehorende afstandenmatrix. En voor de reistijden geldt iets vergelijkbaars.

Is er sprake van éénrichtingsverkeer op één of meer verbindingen, dan onstaat er een gerichte graaf. Pijltjes in de verbindingslijnen geven dan de richting in de graaf aan en je spreekt niet van verbindingen maar van wegen. De bijbehorende directe-wegen-matrix is dan niet symmetrisch meer. De graad van verbinding is nu het aantal wegen gedeeld door het mogelijke aantal wegen.

‡

Voorbeeld 1

Stel de bij deze graaf passende verbindingsmatrix C op en laat door berekening zien dat in C² nog wel nullen voorkomen, maar in C + C² niet meer. Beredeneer ook waarom dit zo is. Hoeveel bedraagt de graad van verbinding en wat betekent dit getal?

Antwoord

Met de knooppunten van links naar rechts en van boven naar beneden in alfabetische volgorde geldt:
C = $\left(\begin{array}{ccccc}0& 0& 0& 0& 1\\ 0& 0& 1& 1& 1\\ 0& 1& 0& 0& 1\\ 0& 1& 0& 0& 1\\ 1& 1& 1& 1& 0\end{array}\right)$, C² = $\left(\begin{array}{ccccc}1& 1& 1& 1& 0\\ 1& 3& 1& 1& 2\\ 1& 1& 2& 2& 1\\ 1& 1& 2& 2& 1\\ 0& 2& 1& 1& 4\end{array}\right)$  en C + C² = $\left(\begin{array}{ccccc}1& 1& 1& 1& 1\\ 1& 3& 2& 2& 3\\ 1& 2& 2& 2& 2\\ 1& 2& 2& 2& 2\\ 1& 3& 2& 2& 4\end{array}\right)$

Elk kental van C² stelt het aantal verbindingen tussen twee knooppunten voor met precies één tussenstation, het aantal tweestapsverbindingen tussen twee punten dus. Tussen E en A bestaat geen twee stapsverbinding. In C + C² komen geen nullen voor omdat tussen elk tweetal knooppunten een één- of een tweestapsverbinding bestaat (soms meerdere).
De graad van verbinding is 6 / 10 = 0,6, dus 60% van alle mogelijke verbindingen bestaat ook echt.

‡

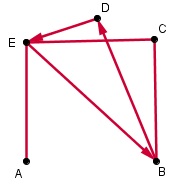
Voorbeeld 2

In deze graaf is sprake van éénrichtingsverkeer.
Stel een bijpassende directe-wegen-matrix D op. Laat zien dat je in maximaal drie stappen (dus met via twee andere knooppunten) van elk punt van de graaf naar elk ander punt kunt komen.

Antwoord

De directe-wegen-matrix is nu niet symmetrisch, dus je moet goed het "van ... naar ..." in de gaten houden. 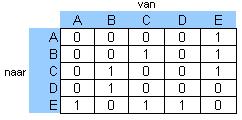Bij deze graaf maak je bijvoorbeeld zo'n schema.
Je vindt dan D = $\left(\begin{array}{ccccc}0& 0& 0& 0& 1\\ 0& 0& 1& 0& 1\\ 0& 1& 0& 0& 1\\ 0& 1& 0& 0& 0\\ 1& 0& 1& 1& 0\end{array}\right)$.

Ga na dat in D en in D + D² nog nullen voorkomen, pas in D + D² + D³ niet meer.
Dit betekent dat inderdaad tussen elke twee knooppunten van de graaf minstens één verbinding bestaat van één of twee of drie stappen.

‡

Voorbeeld 3

Bij een bepaalde graaf met vier knooppunten P, Q, R en S hoort een verbindingsmatrix C met de knooppunten van links naar rechts en van boven naar beneden in alfabetische volgorde.
Teken een bijpassende graaf als: C² = $\left(\begin{array}{cccc}3& 1& 1& 0\\ 1& 2& 1& 1\\ 1& 1& 2& 1\\ 0& 1& 1& 1\end{array}\right)$

Antwoord

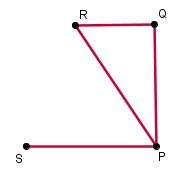
De kentallen van C² geven het aantal tweestapswegen tussen twee punten van de graaf aan.

• Er zijn 3 tweestapswegen van P naar P, dus P is met elk der andere punten verbonden.
• Er is maar 1 tweestapsweg van S naar S, dus S is alleen met P verbonden.
• Er zijn 2 tweestapswegen van Q naar Q, dus Q is met P en R verbonden.
• Er zijn 2 tweestapswegen van R naar R, dus R is met P en Q verbonden.

Nu kun je de graaf maken.

‡

Opgaven

3. Bij een ongerichte graaf kun je een verbindingsmatrix opstellen. Die zegt iets over de mate waarin er verbindingslijnen zijn. In Voorbeeld 1 wordt zo'n verbindingsmatrix `C` gebruikt.
   1. Waarom is hier sprake van een ongerichte graaf?
   2. Reken zelf het voorbeeld na.
   3. De diameter (het maximale aantal stappen dat nodig is om van het éne knooppunt naar het andere te komen) is 2? Hoe zie je dat aan `C + C^2`?
   4. Welke driestapsverbindingen zijn er vanuit knooppunt `C`?
   5. Waarom zijn er maximaal 10 verbindingslijnen mogelijk? Welke verbindingslijnen ontbreken er?


4. Bekijk nu de graaf in Voorbeeld 2.
   1. Waarom is hier sprake van een gerichte graaf?
   2. Hoe kun je aan de directe-wegen-matrix `D` zien dat er sprake is van éénrichtingsverkeer?
   3. Bereken nu `D + D^2` en `D + D^2 + D^3` en leg met behulp van het resultaat uit dat de diameter van deze graaf 3 is.
   4. Geef een voorbeeld van een route die alleen in drie stappen mogelijk is.
   5. Waarom zijn er maximaal 20 directe wegen mogelijk? Hoeveel bedraagt nu de graad van verbinding?


5. Welke van de onderstaande grafen zijn gelijk?
   
   
   
   


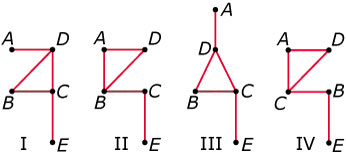
6. In Voorbeeld 3 zie je hoe je vanuit een gegeven tweestapsverbindingsmatrix `C^2` de verbindingsmatrix `C` weer kunt terug vinden.
   1. Ga zelf na, dat de getekende graaf aan de gegeven matrix `C^2` voldoet.
   2. Stel nu de verbindingsmatrix `C` op.
   3. Controleer dat het kwadraat van de verbindingsmatrix `C` inderdaad de gegeven matrix is.


7. Een groep van zes personen moet uit hun midden een woordvoerder kiezen. Ze houden een geheime stemming. Er mag maar op één persoon worden gestemd. De uitslag daarvan vind je in de volgende graaf:
   
   
   
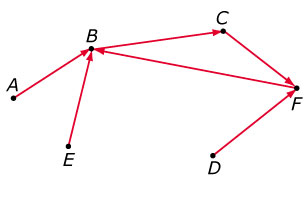
   Stel je voor dat het getal 0 betekent dat iemand niet op de betreffende persoon heeft gestemd en dat het getal 1 betekent dat hij of zij dat juist wel heeft gedaan. De pijl van A naar B betekent dat A op B heeft gestemd.
   1. Is er bij elke uitslag van deze stemming sprake van een gerichte graaf?
   2. Stel een bij de uitslag behorende stemmatrix `K` op.
   3. Wie zou er worden gekozen? Leg uit hoe je dat met behulp van de stemmatrix kunt vaststellen.
   Eén van de zes groepsleden vindt deze stemprocedure niet zorgvuldig genoeg. Zij stelt voor om ieder lid ook een stem met een ‘waarde’ van -1 te laten uitbrengen op de persoon die je absoluut niet ziet zitten als woordvoerder. Opnieuw mag iedereen maar op één persoon een negatieve stem uitbrengen. De volgende graaf geeft de negatieve keuzes weer:
   
   
   
   
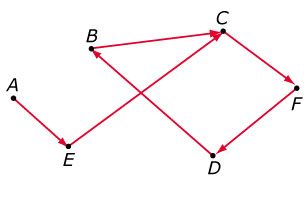
   3. Verwerk ook deze negatieve stemmen in een matrix `N`.
   4. Hoe zou je de matrices `K` en `N` moeten combineren om uit te maken wie er woordvoerder wordt? Licht je antwoord toe.
   5. Levert het combineren van beide matrices een eerlijker stemming op? Verklaar je antwoord.

Verwerken

8. Op Tahiti, een eiland in de Grote Oceaan, bevindt zich alleen langs de kust een hoofdweg die alle plaatsen met elkaar verbindt.
   
   
   
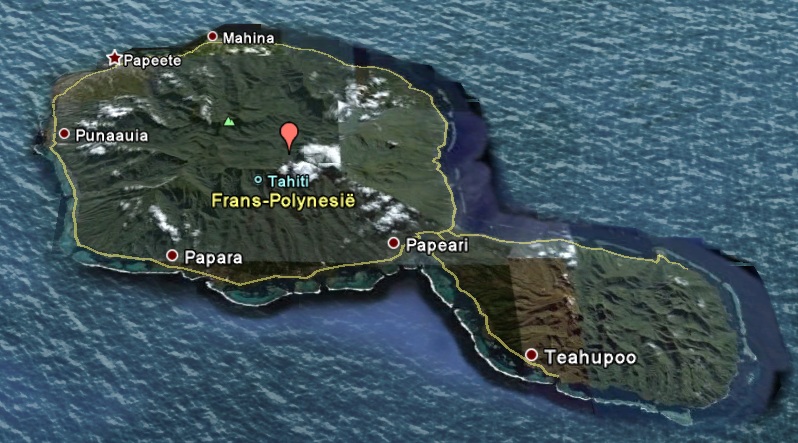
   Je let in deze opgave alleen op de plaatsen Papeete (de hoofdstad), Punaauia, Papara, Papeari en Mahina.
   1. Teken een graaf waarin de genoemde plaatsen de knooppunten vormen en de verbindingslijnen aangeven of twee plaatsen rechtstreeks door de hoofdweg met elkaar verbonden zijn.
   2. Stel de bijbehorende verbindingsmatrix `C` op.
   3. Welke tweestapsverbindingen zijn er vanuit de hoofdstad Papeete?
   4. Bereken `C + C^2`. Welke betekenis heeft deze matrix en waarom komen er geen nullen in voor?
   5. Hoeveel bedraagt de graad van verbinding van deze graaf?
   6. Waarom is de "dichtheid" van deze graaf klein? Klopt dit met de graad van verbinding die je hebt gevonden?


9. In een ontwikkelingsland zijn de verbindingen vaak minimaal. In feite zijn er twee karakteristieke situaties:
   1. Er is in het land één belangrijke stad (meestal de hoofdstad) waar vandaan en naartoe alle verbindingen lopen.
   2. Er is een ringweg aangelegd die alle plaatsen met elkaar verbindt.
   Nu zeg je in een graaf dat er sprake is van minimale verbinding als weliswaar elk knooppunt met minstens één ander knooppunt is verbonden, maar er toch zo weinig mogelijk verbindingen zijn.
   1. Teken bij beide situaties een graaf. Gebruik bij elke situatie 6 knooppunten. Ga na of er bij beide sprake is van minimale verbinding.
   2. Bereken de graad van verbinding in elk van beide situaties.
   3. Bepaal van de beide grafen de diameter. Leg uit welk karakteristieke verschil er bestaat tussen de diameter in situatie 1 en die in situatie 2.
   4. Bekijk de vorige opgave nog eens. Van welke van beide situaties is daar sprake? Waarom is dat op een eiland als Tahiti ook de meest voor de hand liggende oplossing voor de verbindingen?


10. Bij een bepaalde graaf hoort een verbindingsmatrix `C`. Gegeven is:

    `C^2 = ((1 , 1 , 1 , 1 , 0),(1 , 1 , 1 , 1 , 0),(1 , 1 , 1 , 1 , 0),(1 , 1 , 1 , 1 , 0),(0 , 0 , 0 , 0 , 4))`

    1. Welke betekenis heeft het getal 4 in deze matrix?
    2. Teken een bijbehorende graaf. Zijn er meerdere mogelijkheden?
    3. Stel de bij die graaf horende verbindingsmatrix `C` op.
    4. Hoe groot is maximaal aantal stappen dat je nodig hebt om van het éne punt naar het andere te komen in deze graaf?


11. In een woestijngebied liggen een zestal plaatsen in de buurt van oasen. Ze onderhouden met elkaar een netwerk van radioverbindingen. Nu hebben radioverbindingen afhankelijk van de sterkte van de zendinstallatie een beperkt bereik. Het kan dus zijn dat de zender uit plaats A wel sterk genoeg om plaats B te bereiken, maar dat de zender in plaats B niet sterk genoeg is om plaats A te bereiken. De graaf geeft weer of vanuit een bepaalde plaats één van de andere bereikt kan worden met behulp van de radiozender.
    
    
    
    
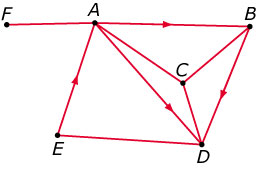
    1. Waarom is er sprake van een gerichte graaf?
    2. Hoeveel uitzendingen zijn er minstens nodig om een bericht van E naar B te sturen door middel van de radiozenders?
    3. Stel een matrix `R` op waarin voor elk tweetal plaatsen staat vermeld of er een rechtstreekse radioverbinding bestaat.
    4. Bereken de matrix `R + R^2 + R^3`. Welke betekenis heeft deze matrix?
    5. Stel een matrix `A` op waarin voor elk tweetal plaatsen het minimale aantal radio-uitzendingen staat dat nodig is om een bericht van de ene naar de andere plaats over te brengen.
    6. Stel je voor dat je in één van deze plaatsen een zendinstallatie mag bouwen die alle andere plaatsen kan bereiken. In welke plaats zou je dat dan doen? Verklaar je antwoord.

Testen

12. In dit berggebied maakte men voor het transport vroeger gebruik van de rivieren en van bergpaden. De rivieren werden gebruikt als er stroomafwaarts goederen moesten worden vervoerd; de bergpaden werden gebruikt als het vervoer stroomopwaarts moest plaatsvinden.
    
    
    
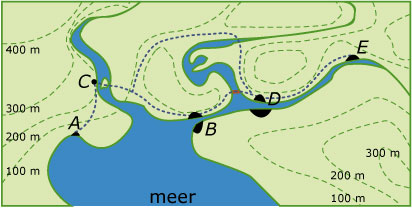
    Je ziet hier de bergpaden en de rivieren waarmee de verbindingen werden onderhouden tussen een vijftal plaatsen. Het meer, waaraan A en B liggen, wordt voor vervoer in beide richtingen gebruikt.
    1. Teken een gerichte graaf van het stelsel van transportwegen tussen deze vijf plaatsen.
    2. Stel bij die graaf een passende directewegenmatrix `R` op.
    3. Welke betekenis heeft de matrix `R + R^2`? Bevat deze matrix nog nullen?
    Tegenwoordig worden de waterwegen niet langer voor vervoer van goederen gebruikt. Alle bergpaden zijn geasfalteerde wegen geworden waarlangs vrachtauto’s heen en weer rijden. Verder is er een snelweg met een grote brug langs het meer aangelegd die A en B met elkaar verbindt.
    4. Teken een nieuwe graaf van transportwegen voor deze situatie.
    5. Stel nu een bijpassende verbindingsmatrix `C` op.
    6. Vanuit punt D moet je om in B te komen via E rijden. Dit kun je een tweestapsverbinding vanuit D noemen. Schrijf alle tweestapsverbindingen vanuit B op.
    7. Hoe groot is de graad van verbinding van de graaf?
    8. Hoeveel nullen bevat de matrix `C + C^2`? Verklaar waarom dit zo is.