Grafen

Antwoorden bij de opgaven

  1. .
    1. `C = ((0 , 1 , 0 , 1 , 1 , 1),(1 , 0 , 1 , 1 , 1 , 0),(0 , 1 , 0 , 0 , 0 , 0),(1 , 1 , 0 , 0 , 0 , 0),(1 , 1 , 0 , 0 , 0 , 0),(1 , 0 , 0 , 0 , 0 , 0))`
    2. `8/15`
    3. Tussen 0 en 1. Er is een hoge dichtheid van de verbindingen als de verbindingsgraad dicht bij 1 ligt.
    4. `C^2 = ((4 , 2 , 1 , 1 , 1 , 0),(2 , 4 , 0 , 1 , 1 , 1),(1 , 0 , 1 , 1 , 1 , 0),(1 , 1 , 1 , 2 , 2 , 1),(1 , 1 , 1 , 2 , 2 , 1),(0 , 1 , 0 , 1 , 1 , 1))`
    5. CS–ZW–CS, CS–WW–CS, CS–GN–CS en CS–GA–CS.
    6. `C + C^2 = ((4 , 3 , 1 , 2 , 2 , 1),(3 , 4 , 1 , 2 , 2 , 1),(1 , 1 , 1 , 1 , 1 , 0),(2 , 2 , 1 , 2 , 2 , 1),(2 , 2 , 1 , 2 , 2 , 1),(1 , 1 , 0 , 1 , 1 , 1))`. Van de Isolatorweg naar de Gaasperplas v.v. kan niet in één of twee stappen.
    7. CS–ZW–GN–CS, CS–GN–ZW–CS, CS–GN–WW–CS en CS–WW–GN–CS.
    8. Nee, elk knooppunt is in drie of minder stappen verbonden met elk ander knooppunt.
    1. 3
    2. Alleen Isolatorweg en Gaasperplas.
    1. Er wordt steeds van uit gegaan dat verkeer in beide richtingen mogelijk is.
    2. Doen, gebruik je grafische rekenmachine.
    3. Er komen in `C + C^2` geen nullen meer voor.
    4. C–B–E–C en C–E–B–C.
    5. het maximale aantal verbindingslijnen is `5 * 4 // 2 = 10`. Ontbrekende verbindingen zijn A–B, A–C, A–D en C–D.
    1. De pijlen geven éénrichtingsverkeer aan.
    2. Hij is niet symmetrisch in de hoofddiagonaal.
    3. `D + D^2 = ((1 , 0 , 1 , 1 , 1),(1 , 1 , 2 , 1 , 2),(1 , 1 , 2 , 1 , 2),(0 , 1 , 1 , 0 , 1),(1 , 2 , 1 , 1 , 2))` en `D + D^2 + D^3 = ((1 , 2 , 1 , 1 , 3),(2 , 3 , 4 , 2 , 5),(2 , 4 , 3 , 2 , 5),(1 , 2 , 2 , 1 , 2),(3 , 2 , 5 , 3 , 4))`. Omdat in `D + D^2 + D^3` voor het eerst geen nullen meet voorkomen is elk knooppunt met elk ander knooppunt verbonden in 3 of minder stappen.
    4. De kortste route van D naar C.
    5. `5 * 4 = 20`, vanuit elk knooppunt zijn er 4 directe wegen naar een ander knooppunt. De graad van verbinding is `9/20`.
  5. De grafen I, III en IV zijn gelijk. Het zijn eigenlijk allemaal driehoeken met aan twee hoekpunten nog een extra verbindingsweg.
    1. Doen.
    2. `C = ((0 , 1 , 1 , 1),(1 , 0 , 1 , 0),(1 , 1 , 0 , 0),(1 , 0 , 0 , 0))`
    3. Even nagaan door `C^2` te berekenen vanuit het antwoord bij b.
    1. Ja. Als `A` op `B` heeft gestemd, wil dat niet zeggen dat `B` ook op `A` heeft gestemd.
    2. `K = ((0 , 1 , 0 , 0 , 0 , 0),(0 , 0 , 1 , 0 , 0 , 0),(0 , 0 , 0 , 0 , 0 , 1),(0 , 0 , 0 , 0 , 0 , 1),(0 , 1 , 0 , 0 , 0 , 0),(0 , 1 , 0 , 0 , 0 , 0))`
      als de knooppunten op een rij van links naar rechts en in een kolom van onder naar boven alfabetisch zijn gerangschikt.
    3. `B` zou gekozen worden. Hij krijgt de meeste stemmen, zie de som van de kentallen van de tweede kolom.
    4. `N = ((0 , 0 , 0 , 0 , -1 , 0),(0 , 0 , -1 , 0 , 0 , 0),(0 , -1 , 0 , 0 , 0 , 0),(0 , -1 , 0 , 0 , 0 , 0),(0 , 0 , -1 , 0 , 0 , 0),(0 , 0 , 0 , -1 , 0 , 0))`
    5. De matrices `K` en `N` optellen. Bepaal de som van de kentallen van de kolommen. Je vindt: `0, 1, -1, -1, -1` en 2. `F` zal nu gekozen worden.
    6. Eigen antwoord.
  8. In deze antwoorden wordt de volgorde Papeete (de hoofdstad), Punaauia, Papara, Papeari en Mahina gebruikt.
    1. Doen.
    2. `C = ((0 , 1 , 0 , 0 , 1),(1 , 0 , 1 , 0 , 0),(0 , 1 , 0 , 1 , 0),(0 , 0 , 1 , 0 , 1),(1 , 0 , 0 , 1 , 0))`
    3. Papeete - Punaauia - Papeete; Papeete - Mahina - Papeete;
    4. `C + C^2 = ((2 , 1 , 1 , 1 , 1),(1 , 2 , 1 , 1 , 1),(1 , 1 , 2 , 1 , 1),(1 , 1 , 1 , 2 , 1),(1 , 1 , 1 , 1 , 2))`
      Deze matrix geeft aan of plaatsen met elkaar zijn verbonden in één of twee stappen. Kennelijk is dat altijd het geval.
    5. Er zijn 5 knooppunten, dus er zijn in totaal 10 wegen mogelijk. Er zijn er slechts 5 getekend. De graad van verbinding is: `5/10 = 0,5`.
    6. Er zijn veel plaatsen die niet rechtstreeks met elkaar verbonden zijn.
    1. Zie de figuur.
    2. In de eerste graaf is de verbinding minimaal.
    3. In de eerste graaf is de graad van verbinding `5/15 = 1/3` en bij de tweede graaf `6/15 = 2/5`.
    4. De diameter in de eerste graaf is 2 en in de tweede is hij 3.
    5. De tweede graaf; omdat het eiland erg bergachtig is in het binnenland en alle plaatsen langs de kust liggen.
    1. Er zijn 4 tweestapsverbindingen van dat punt naar zichzelf.
    2. Zie de figuur.
    3. `C = ((0 , 0 , 0 , 0 , 1),(0 , 0 , 0 , 0 , 1),(0 , 0 , 0 , 0 , 1),(0 , 0 , 0 , 0 , 1),(1 , 1 , 1 , 1 , 0))`
    4. In de graaf is te zien dat de diameter 2 is.
    1. Er zijn verbindingen die een richting hebben.
    2. Van `E` naar `D` naar `C` naar `B`. Er zijn dus 3 uitzendingen nodig.
    3. `R = ((0 , 1 , 1 , 1 , 1 , 1),(0 , 0 , 1 , 1 , 0 , 0),(1 , 1 , 0 , 1 , 0 , 0),(0 , 0 , 1 , 0 , 1 , 0),(0 , 0 , 0 , 1 , 0 , 0),(1 , 0 , 0 , 0 , 0 , 0))`
    4. `R + R^2 + R^3 = ((4 , 6 , 9 , 10 , 7 , 3),(2 , 3 , 5 , 6 , 3 , 1),(5 , 5 , 6 , 9 , 4 , 1),(1 , 2 , 5 , 4 , 4 , 1),(1 , 1 , 1 , 3 , 1 , 0),(3 , 2 , 3 , 4 , 2 , 1))`
      Deze matrix geeft het aantal éénstaps-, tweestaps- of driestapsverbindingen tussen twee plaatsen.
    5. `A = ((1 , 1 , 1 , 1 , 1 , 1),(2 , 1 , 1 , 1 , 2 , 3),(1 , 1 , 1 , 1 , 2 , 2),(2 , 2 , 1 , 1 , 1 , 3),(3 , 3 , 2 , 1 , 1 , 4),(1 , 2 , 2 , 2 , 2 , 1))`
    6. Tel de kentallen van de rijen in matrix `A` op. Je vindt dan: 6, 10, 8, 10, 14 en 10. Plaats de zender in `E`, want je hebt vanuit `E` de meeste uitzendingen nodig.
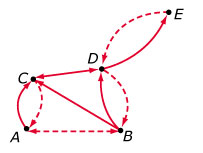
    1. Zie figuur. De waterwegen zijn gestippeld.
    2. `R = ((0 , 1 , 1 , 0 , 0),(1 , 0 , 1 , 1 , 0),(1 , 0 , 0 , 1 , 0),(0 , 1 , 1 , 0 , 1),(0 , 0 , 0 , 1 , 0))`
    3. `R + R^2` geeft het totaal van alle één- en tweestapsverbindingen. Er komen nog nullen in voor, want `A` – `E` is een driestapsverbinding.
    4. Doen.
    5. `C = ((0 , 1 , 1 , 0 , 0),(1 , 0 , 1 , 1 , 0),(1 , 1 , 0 , 1 , 0),(0 , 1 , 1 , 0 , 1),(0 , 0 , 0 , 1 , 0))`
    6. De tweestapsverbindingen van uit `E` zijn: `E` – `D` - `E`, `E` – `D` - `C` en `E` – `D` - `B`.
    7. De graad van verbinding van de graaf is 0,6.
    8. Er komen nog twee nullen in voor, want `A` – `E` en `E` – `A` zijn driestapsverbindingen.