Matrixvermenigvuldiging

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Discrete wiskunde > Matrices en grafen > Matrixvermenigvuldiging > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Discrete wiskunde > Matrices en grafen > Matrixvermenigvuldiging > Uitleg

Opgaven

1. Bekijk in de Uitleg hoe een winkelier in Excel een bestelling van een bepaald type wandelschoen bijhoudt. Met matrixvermenigvuldiging worden in één klap zowel de inkoopprijs als de verkoopprijs per variant berekend.
   1. Voer zelf die matrixvermenigvuldiging handmatig uit.
   2. Voer beide matrices in je rekenmachine in en controleer dat je na ze te vermenigvuldigen dezelfde uitkomst krijgt als bij a.
   3. Waarom is het van belang dat je de prijzen in een 3×2-matrix weergeeft als de voorraadmatrix een 4×3-matrix is?
   4. Als je in de voorraadmatrix de volgorde van de varianten verwisselt, heeft dit dan gevolgen voor de prijzenmatrix?
   5. Als je in de prijzenmatrix de volgorde van de inkoop- en de verkoopprijs verwisselt, heeft dit dan gevolgen voor de voorraadmatrix?


2. Bekijk nog eens de matrixvermenigvuldiging in de vorige opgave.
   1. Je geeft de voorraadmatrix V weer in een 3×4-matrix. Hoe moet je dan de prijzenmatrix P maken?
   2. Hoe moet je nu de matrixvermenigvuldiging uitvoeren en wat voor matrix is het resultaat?
   3. Voer die matrixvermenigvuldiging met je rekenmachine uit. (Je kunt daarvoor de matrices van de vorige opgave gebruiken door ze te transponeren!)

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Discrete wiskunde > Matrices en grafen > Matrixvermenigvuldiging > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

3. In Voorbeeld 1 zie je hoe twee matrices worden vermenigvuldigd.
   1. Voer zelf handmatig de berekening `B * P` uit. Controleer je antwoord met behulp van je rekenmachine.
   2. Voer nu ook de berekening `P^T * B^T` uit. Waarin verschilt het antwoord met dat bij a?
   3. Is `P * B` een mogelijke matrixvermenigvuldiging? Waarom?


4. Gegeven zijn de volgende matrices

   `A = ((3 , -2),(0 , 8),(1 , 7))`, `B = ((3 , 2),(5 , 7))`, `C = ((10 , 8),(20 , 0),(7 , 15))`, `D = ((1 , 8 , 0 , 3),(0 , 2 , 7 , 5))` en `E = ((0),(1))

   Bereken, voorzover dat mogelijk is: `A * B`, `A * C`, `A * D`, `A * E`, `B * D`, `B * C`, `B * B`, `C * C`, `C * B`, `B * A`.
   Bekijk eventueel eerst Voorbeeld 2.
   


5. Gebruik de matrices `A` en `B` uit de voorgaande opgave.
   1. Is de matrixvermenigvuldiging `B * A^T` mogelijk?
   2. Voer deze matrixvermenigvuldiging nog eens handmatig uit. Controleer je antwoord met de rekenmachine.


6. In Voorbeeld 3 zie je hoe je machten van matrices berekent.
   1. Bereken `A^2` handmatig. Controleer je antwoord met de rekenmachine.
   2. Hoe moet je nu `A^3` handmatig berekenen?
   3. Bereken `B^4` met de grafische rekenmachine.
   4. Kun je van elke matrix machten berekenen? Licht je antwoord toe.
   5. Vermenigvuldig `A` met de 3×3-eenheidsmatrix `E_3`. Wat is het resultaat?
   6. Maakt het verschil of je `A * E_3` of `E_3 * A` uitrekent?


7. Een fabrikant van filterkoffie heeft drie variëteiten in de handel, te weten "Roodmerk", "Zilvermerk" en "Goudmerk". In een bepaalde stad verkoopt een supermarktketen de verschillende variëteiten koffie in drie filialen. In een centraal magazijn worden de voorraden opgeslagen. Daar wordt ook per filiaal de voorraad beheerd. Elke dag worden de filialen vanuit dat centrale magazijn bevoorraad. De volgende tabel geeft de vooraad per filiaal, de inkoopprijs en de verkoopprijs van elk van de drie koffievarianten weer.
   
   

   	Roodmerk	Zilvermerk	Goudmerk
   filiaal 1	400	200	600
   filiaal 2	500	400	0
   filiaal 3	500	700	200
   inkoopprijs	4,70	4,90	5,25
   verkoopprijs	5,15	5,30	5,90

   
   
   De voorraadgegevens zijn van maandagochtend.
   Je kunt nu op verschillende manieren een prijsmatrix `P` opstellen, waarin per variant de inkoopprijs en de verkoopprijs staan.
   1. Hoe moet die`P` eruit zien als je met behulp van matrixvermenigvuldiging de totale inkoopprijs en de totale verkoopprijs van de voorraad op maandagochtend per filiaal wilt berekenen?
   2. Kun je ook met matrixvermenigvuldiging de totale inkoopprijs en verkoopprijs per variant berekenen? Zo ja, laat dit dan zien.
   Hier zie je wat er die maandag aan koffie werd verkocht:
   
   

   	Roodmerk	Zilvermerk	Goudmerk
   filiaal 1	264	300	410
   filiaal 2	306	233	391
   filiaal 3	412	530	199

   
   
   
   3. Stel een winstmatrix per koffievariant op. Doe dat zo dat je de winst op de koffieverkoop op de maandag per filiaal kunt berekenen.
   4. Bereken ook de winst per koffie variëteit op de totale verkoop van deze maandag.


8. Iemand heeft bij de voorgaande opgave de volgende voorraadmatrix `V` en prijsmatrix `M` gemaakt:

   `V = ((400 , 200 , 600),(500 , 400 , 0),(500 , 700 , 200))` en `M = ((4,70 , 4,90 , 5,25),(5,15 , 5,30 , 5,90),(0,45 , 0,40 , 0,65))`

   Hij berekent nu `V * M`. Is dat mogelijk? Krijgt hij getallen die betekenis hebben?
   

Verwerken

9. Gegeven zijn de matrices:

   `A = ((4 , 3 , 1 , 9),(2 , 0 , 5 , 10),(12 , 5 , 7 , 6))`, `B = ((5 , 2),(0 , 4),(1 , 7),(8 , 3))` en `C = ((6 , 4),(8 , 2))`

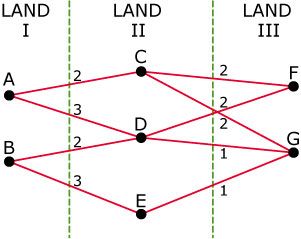
   Bereken indien mogelijk de volgende matrices:
   1. `A * B` en `B * A`
   2. `B * 0, 5 * C`
   3. `C^3`
   4. `C^4 * B`
   5. `B + C`



van	naar	prijs (€)
A	C	500
A	D	810
B	D	1020
B	E	598
C	F	390
C	G	612
D	F	185
D	G	142
E	G	420

10. Je ziet hier het aantal vluchten per dag tussen vliegvelden in drie verschillende landen in beeld gebracht.
    
    
    
    De tabel geeft de vluchttarieven tussen deze vliegvelden weer.
    1. Stel een 2×3-matrix `V_1` op die het aantal dagelijkse vluchten van land I naar land II weergeeft.
    2. Stel een matrix `V_2` op die het aantal dagelijkse vluchten van land II naar land III weergeeft. Zorg ervoor dat `V_2` zo wordt samengesteld, dat `V_1 * V_2` betekenis heeft.
    3. Bereken `V_1 * V_2` en omschrijf de betekenis van die matrix.
    4. Stel een 2×3-matrix `T_1` op die de vluchttarieven van land I naar land II beschrijft.
    5. Stel een vluchttarievenmatrix `T_2` op die de vluchttarieven van land II naar land III beschrijft.
    6. Stel tenslotte een matrix op waarin je de vluchttarieven van land I via land II naar land III weergeeft. Kun je die matrix laten ontstaan door op `T_1` en `T_2` een matrixbewerking toe te passen?


11. Veel mensen werken in een andere plaats dan ze wonen. Deze forensen gebruiken vaak de auto voor het woon-werkverkeer. Hier wordt een model van zo'n situatie geschetst,waarin vier steden en hun onderlinge verbindingswegen een rol spelen. De getallen geven de rij-afstanden in km weer. De tabel geeft het aantal forensen weer dat 's morgens naar het werk gaat.
    
    

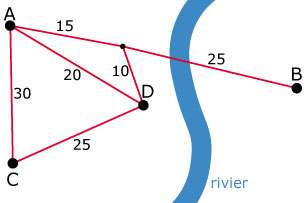
    		naar
    		A	B	C	D
    van	A	0	400	350	200
    	B	200	0	100	50
    	C	150	200	0	100
    	D	100	50	150	0

    
    
    1. Stel een afstandenmatrix `M` bij dit model op.
    2. Stel een forensenmatrix `F` op zo, dat de vermenigvuldiging `M * F` mogelijk is.
    3. Bereken `M * F`. Zijn er kentallen in deze matrix die betekenis hebben?
    4. Bepaal het totaal aantal km dat deze forensen op één dag afleggen, ervan uitgaande dat ze allen na het werk weer via de kortste route naar huis teruggaan.
    5. Als je alleen de benzinekosten rekent, hoeveel kost dit forensenverkeer dan elke dag? Ga ervan uit dat een auto gemiddeld 1 : 15 rijdt en een liter benzine € 1,20 kost.
    6. Er wordt een rechtstreekse verbinding met een nieuwe brug van B naar C aangelegd met een lengte van 50 km. Hoeveel besparing in de dagelijkse benzinekosten levert dat op?


12. Kijk nog eens naar de afstandenmatrix `M` uit de voorgaande opgave. Een bepaald bedrijf dat in C is gevestigd heeft werknemers uit elk van deze vier plaatsen in dienst. Vanuit A werken er 150 mensen bij dit bedrijf, er wonen 50 werknemers in B en 100 in D. Deze mensen rijden dagelijks heen en weer naar het bedrijf, dat de reiskosten voor hun woon-werkverkeer vergoedt. De 200 werknemers die in C wonen, krijgen geen reiskosten vergoed.
    1. Stel een matrix `W` op voor het aantal werknemers van het bedrijf per plaats.
    2. Vermenigvuldig de matrices `M` en `W` op de juiste manier. Welke betekenis heeft de productmatrix?
    3. Hoe kun je nu vaststellen of het bedrijf zich beter in één van de drie andere plaatsen kan vestigen vanuit het oogpunt van de reiskostenvergoeding?


13. Gebruik een willekeurige 3×3-matrix `A = ((a , b , c),(d , e, f),(g , h , i))`.
    `E_3` stelt de 3×3-eenheidsmatrix voor.
    1. Vermenigvuldig `A` met `E_3`. Wat gebeurt er? Maakt de volgorde waarin je vermenigvuldigt daarbij uit?
    2. Verwissel in `E_3` de tweede en de derde kolom. Je krijgt dan matrix `M_1`. Bereken `M_1 * A` en `A * M_1`. Verklaar beide resultaten.
    3. Vervang in `E_3` het kental in de eerste rij en de eerste kolom in een 2. Je krijgt dan matrix `M_2`. Bereken `M_2 * A` en `A * M_2`. Verklaar beide resultaten.
    Je ziet dat je met matrixvermenigvuldiging, door `E_3` op een geschikte wijze aan te passen, `A` kunt veranderen in een matrix waarbij twee kolommen of twee rijen zijn verwisseld of waarbij één kolom of rij met een bepaald getal is vermenigvuldigd.
    1. Experimenteer met je grafische rekenmachine en samen met een medeleerling. Verzin een paar regels voor dit verschijnsel.
    2. Je wilt matrix A veranderen in een matrix waarin de tweede kolom met 3 wordt vermenigvuldigd en de laatste twee rijen zijn verwisseld. Is dat mogelijk met matrixvermenigvuldiging? Zo ja, laat dan zien hoe.

Testen

14. Gegeven zijn de matrices

    `A = ((5 , -1 , 3),(0 , 2 , 1))` en `B = ((7 , 2 , 0),(0 , 3 , 1),(1 , 4 , 1))`

    Bereken nu voor zover dat mogelijk is:
    1. `2 * A * B`
    2. `2 * B * A`.
    3. `B^2`
    4. `B + B^2`
    5. `A^3`


15. Een bepaald type muurverf wordt in vijf tinten geproduceerd. Die tinten onstaan door het mengen van drie kleurstoffen in verschillende verhoudingen. De volgende tabel geeft weer in welke verhouding de kleurstoffen worden gemengd voor elk van de vijf tinten.
    
    

    		Kleurstof
    		A	B	C
    tint	a	0,40	0,40	0,20
    	b	0	0,50	0,50
    	c	0,15	0,55	0,30
    	d	0,60	0,20	0,20
    	e	0,80	0	0,20

    
    De productie per maand is: 1200 liter van tint a, 1600 liter van tint b, 950 liter van tint c, 1750 liter van tint d en 1300 liter van tint e.
    1. Stel een mengmatrix `M` en een productiematrix `P` op zo, dat `M * P` betekenis heeft.
    2. Bereken `M * P` en omschrijf de betekenis van deze matrix.
    De kosten voor de kleurstoffen bedragen:
    • kleurstof A: € 52,- per liter,
    • kleurstof B: € 24,- per liter,
    • kleurstof C: € 46,- per liter.
    3. Stel een kostenmatrix `K` voor de kleurstoffen op zo, dat `K * M * P` betekenis heeft.
    4. Bereken `K * M * P` en omschrijf de betekenis van die matrix.
    5. Maakt het verschil of je dit product berekent als `(K * M) * P` of als `K * (M * P)`?
    6. Bereken `M * P * K`. Zijn er getallen in deze matrix te vinden die betekenis hebben?