Het begrip matrix

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Discrete wiskunde > Matrices en grafen > Het begrip matrix > Inleiding

Probeer de vraag bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Discrete wiskunde > Matrices en grafen > Het begrip matrix > Uitleg

Opgaven

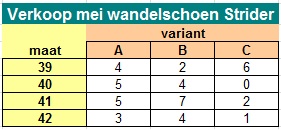1. Bekijk in de Uitleg hoe een winkelier in Excel zijn vooraad van een bepaald type wandelschoen bijhoudt. Ga er van uit dat de voorraad is geteld op 31 april. Voordat zijn bestelling is aangekomen zijn er in mei al weer schoenen van het model "Strider" verkocht. De tabel hiernaast geeft dat weer.
   1. Schrijf de bijbehorende verkoopmatrix op.
   2. Welk getal staat op de derde rij en in de tweede kolom?
   3. Bereken de nieuwe voorraadmatrix op het moment dat de bestelling op 1 juni binnenkomt. Welke matrixbewerkingen passen hierbij?

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Discrete wiskunde > Matrices en grafen > Het begrip matrix > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

2. In de Theorie wordt het begrip matrix ingevoerd. Hier zie je de matrix

   $M=\left(\begin{array}{cccc}1& 7& 6& 2\\ 3& 6& 0& 4\end{array}\right)$

   1. Hoeveel kentallen heeft matrix `M`?
   2. Hoeveel kolommen heeft matrix `M`?
   3. Hoeveel rijen heeft deze matrix?
   4. Welk kental staat er in de tweede rij en in de derde kolom?
   5. Schrijf matrix `M^T` op.


3. In Voorbeeld 1 wordt de voorraad berekend met behulp van twee 2 × 5-matrices van elkaar af te trekken..
   1. Geef zowel de voorraad als de verkoop kan in een 5 × 2-matrix worden weergegeven. Doe dat en bereken de nieuwe voorraadmatrix.
   2. Bekijk via

      www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Discrete wiskunde > Matrices en grafen > Het begrip matrix > Inleiding

      hoe je matrices in je grafische rekenmachine invoert.
   3. Voer de matrixoptelling van a ook met de grafische rekenmachine uit.


4. Gegeven zijn de volgende matrices

   $A=\left(\begin{array}{cc}2& -3\\ 1& 6\\ 0& 5\end{array}\right)$, $B=\left(\begin{array}{ccc}3& 20& 15\\ 5& 12& 10\end{array}\right)$ en $C=\left(\begin{array}{cc}10& 8\\ 20& 0\\ 7& 15\end{array}\right)$.

   1. Welk getal is `c_(3,1)`?
   2. Bereken voor zover mogelijk `A + C`, `A + B`, `5A - C`.
   3. In Voorbeeld 2 zie je hoe je matrices soms kunt optellen door eerst te transponeren. Bereken `A + B^T`.
   4. Ga ook na hoe dit op de grafische rekenmachine gaat.


5. In Voorbeeld 3 zie je dat een zwart-wit-plaatje (als bitmap) eigenlijk een grote matrix is. Werk met de 6 × 6-matrix die in het voorbeeld is gegeven.
   1. Maak het plaatje 30% donkerder en bereken de nieuwe pixelwaarden (op gehelen nauwkeurig).
   2. Waarom kun je bij a alle kentallen van de matrix met hetzelfde getal vermenigvuldigen en kon dit in het voorbeeld niet?

Verwerken

6. Een fabrikant van filterkoffie heeft drie variëteiten in de handel, te weten "Roodmerk", "Zilvermerk" en "Goudmerk". In een bepaalde stad verkoopt een supermarktketen de verschillende variëteiten koffie in drie filialen. In een centraal magazijn worden de voorraden opgeslagen. Daar wordt ook per filiaal de voorraad beheerd. Elke dag worden de filialen vanuit dat centrale magazijn bevoorraad. De volgende tabel geeft de vooraad per filiaal, de inkoopprijs en de verkoopprijs van elk van de drie koffievarianten weer.
   
   

   	Roodmerk	Zilvermerk	Goudmerk
   filiaal 1	400	200	600
   filiaal 2	500	400	0
   filiaal 3	500	700	200
   inkoopprijs	4,70	4,90	5,25
   verkoopprijs	5,15	5,30	5,90

   
   
   De voorraadgegevens zijn van maandagochtend.
   1. Stel een voorraadmatrix `V` op waarin de voorraad per variant per filiaal op maandagochtend staat.
   De filialen krijgen meteen op maandagochtend nieuwe voorraad. De volgende tabel geeft de bestelling weer:
   
   

   	Roodmerk	Zilvermerk	Goudmerk
   filiaal 1	200	100	0
   filiaal 2	100	200	400
   filiaal 3	100	0	300

   
   
   
   2. Stel de bijbehorende bestelmatrix `B` op. Doe dit zo dat `V + B` betekenis heeft.
   3. Bereken `V + B`. Welke betekenis heeft `V + B`?
   Hier zie je wat er die maandag aan koffie werd verkocht:
   
   

   	Roodmerk	Zilvermerk	Goudmerk
   filiaal 1	264	300	410
   filiaal 2	306	233	391
   filiaal 3	412	530	199

   
   
   
   4. Stel de verkoopmatrix `K` op. Doe dit zo dat `V + B - K` betekenis heeft.
   5. Bereken `V + B - K`. Welke betekenis heeft `V + B - K`?
   Je kunt nu op verschillende manieren een prijsmatrix `P` opstellen, waarin per variant de inkoopprijs en de verkoopprijs staan.
   6. Stel een prijsmatrix `P` op.
   7. Hoe kun je met die prijsmatrix en de verkoopmatrix berekenen hoeveel de verkoop op maandag per filiaal aan winst heeft opgebracht?
   8. Hoe kun je met die prijsmatrix en de verkoopmatrix berekenen hoeveel de verkoop op maandag per koffievariant aan winst heeft opgebracht?


7. Gegeven zijn de matrices

   $A=\left(\begin{array}{ccc}3& 3& 1\\ 2& 11& 5\\ -1& 5& 7\end{array}\right)$, $B=\left(\begin{array}{ccc}3& 4& -2\\ 12& -4& 5\\ 7& 10& 8\end{array}\right)$ en $C=\left(\begin{array}{cc}-5& 10\\ -12& 6\\ 15& -8\end{array}\right)$.

   1. Welk getal is `b_(2,3)`?
   2. Bereken indien mogelijk `A + B`, `B - 2A`, `A + 3C`.
   3. Waarom kun je bij deze matrices zowel `A + B` als `A^T + B` berekenen?
   4. Bereken `2A + B^T`.


8. Een bedrijf heeft vestigingen in Apeldoorn, Deventer en Zutphen. De afstanden tussen deze vestigingen bedragen:
   • Van de vestiging in Apeldoorn naar die in Deventer 17 km.
   • Van de vestiging in Zutphen naar die in Deventer 13 km.
   • Van de vestiging in Apeldoorn naar die in Zutphen 26 km.
   1. Geef de afstanden tussen de vestigingen weer in een 3 × 3-matrix `A`.
   2. De gemiddelde reistijd tussen deze plaatsen is 40 km/uur. Stel een reistijdenmatrix `R` tussen de vestigingen van dit bedrijf op. Geef de reistijden in minuten.
   3. Waarom zal matrix `R` zeer waarschijnlijk geen erg betrouwbare reistijden weergeven?

Testen

9. Gegeven zijn de matrices

   $A=\left(\begin{array}{ccc}5& -2& 1\\ 6& 10& 5\end{array}\right)$, $B=\left(\begin{array}{ccc}10& 8& -5\\ 12& -5& 10\end{array}\right)$ en $C=\left(\begin{array}{cc}-5& 10\\ -12& 6\\ 15& -8\end{array}\right)$.

   1. Welk getal is `a_(1,2)`?
   2. Bereken indien mogelijk `A + B`, `B + C`, `3A - 2B`.
   3. Waarom kun je bij deze matrices wel `A + C^T` maar niet `A + C` berekenen?
   4. Bereken `A + C^T`.


10. Autobedrijf Dankers verkoopt de Smart Fortwo zowel in filiaal Noord als in filiaal Zuidwijk. De Smart Fortwo is er in verschillende uitvoeringen: de "pure", de "pulse", de "passion" en de "Brabus". De verkoopcijfers voor filiaal Noord waren in mei achtereenvolgens 4 keer de pure, 5 keer de pulse, 8 keer de passion en 2 keer de Brabus. In juni waren de verkoopcijfers in dezelfde volgorde 5, 3, 7 en 1 stuks. Voor filiaal Zuidwijk waren de verkoopcijfers in mei 8 pure, 6 pulse, 9 passion en 5 Brabus en in juni 10 pure, 5 pulse, 11 passion en 4 Brabus.
    1. Geef de verkoopcijfers van filiaal Noord weer in een 2 × 4-matrix `N`.
    2. Geef de verkoopcijfers van filiaal Zuidwijk in eenzelfde matrix `Z` weer.
    3. Bereken `N + Z`. Welke betekenis heeft deze matrix?
    4. Hoe kun je de totale verkoopcijfers van beide filialen samen berekenen?