Het begrip matrix

Antwoorden bij de opgaven

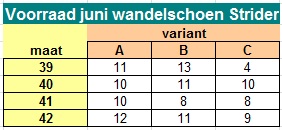
    1. `V = ((4 , 2 , 6),(5 , 4 , 0),(5 , 7 , 2),(3 , 4 , 1))`
    2. 7
    3. Zie de figuur hiernaast.
    1. 8
    2. 4
    3. 2
    4. 0
    5. `M^T = ((1 , 3),(7, 6),(6 , 0),(2 , 4))`
    1. `((8 , 3),(15 , 10),(12 , 13),(7 , 8),(4 , 2)) - ((3 , 1),(4 , 8),(2 , 9),(5 , 0),(0 , 2)) = ((5 , 2),(11 , 2),(10 , 4),(2 , 8),(4 , 0))`
    2. Bekijk het genoemde practicum!
    3. Doen.
    1. 7
    2. `A + C = ((12 , 5),(21 , 6),(7 , 20))`, `A + B` kan niet, `5A - C = ((0 , -7),(-15 , 30),(-7 , 10))`
    3. `A + B^T = ((5 , 2),(21 , 18),(15 , 15))`
    4. Doen.
  5. Denk om het afronden op gehele pixels.
    1. ((51 , 71 , 26 , 77 , 66, 0),(20 , 41 , 5 , 51 , 36 , 20),(66 , 0 , 71 , 41 , 0 , 77),(36 , 77 , 26 , 51 , 41 , 71),(71, 5 , 66 , 20 , 36 , 77),(26 , 51 , 36 , 66 , 5 , 41))
    2. Omdat je altijd waarden krijgt vanaf 0 t/m 255.
    1. `V = ((400 , 200 , 600),(500 , 400 , 0),(500 , 700 , 200))`
    2. `B = ((200 , 100 , 0),(100 , 200 , 400),(100 , 0 , 300))`
    3. `V + B = ((600 , 300 , 600),(600 , 600 , 400),(600 , 700 , 500))` is de nieuwe voorraad als de bestelling binnen is.
    4. `K = ((264 , 300 , 410),(306 , 233 , 391),(412 , 530 , 199))`
    5. `V + B - K = ((336 , 0 , 190),(294 , 367 , 9),(188 , 170 , 301))` is de nieuwe voorraad na de verkoop op maandag.
    6. Bijvoorbeeld: `P = ((4,70 , 4,90 , 5,25),(5,15 , 5,30 , 5,90))`
    7. Dat is nog een heel werk. Om bijvoorbeeld de winst voor filiaal 1 te berekenen moet je eerst de inkoopprijs per soort koffie van de verkoopprijs aftrekken en dit dan vermenigvuldigen met het aantal pakken dat je van die soort hebt verkocht.
    8. Om bijvoorbeeld de winst op de soort Roodmerk te berekenen moet je eerst de inkoopprijs van Roodmerk van de verkoopprijs aftrekken en dit dan vermenigvuldigen met het aantal pakken dat je van die soort per filiaal hebt verkocht en dit bij elkaar optellen.
    1. `b_(2,3) = 5`
    2. `A + B = ((6 , 7 , -1),(14 , 7 , 10),(6 , 15 , 15))` en `B - 2A = ((-3 , -2 , -4),(8 , -26 , -5),(9 , 0 , -6))`. `A + 3C` kan niet.
    3. Omdat `A` een vierkante matrix is, hij heeft evenveel rijen als kolommen.
    4. `2A + B^T = ((9 , 18 , 9),(8 , 18 , 20),(-4 , 20 , 22))`
    1. `A = ((0 , 17 , 26),(17 , 0 , 13),(26 , 13 , 0))`
    2. `1,5 A = ((0 , 25,5 , 39),(25,5 , 0 , 19,5),(39 , 19,5 , 0))`
    3. De snelheid van 40 km/uur is een gemiddelde met waarschijnlijk een grote bijbehorende spreiding.
    1. `a_(1,2) = -2`
    2. `A + B = ((15 , 6 , -4),(18 , 5 , 15))`, `B + C` kan niet en `3A - 2B = ((-5 , -22 , 13),(-6 , 40 , -5))`
    3. Omdat `A` en `C^T` allebei 2×;3-matrices zijn en `A` en `C` niet dezelfde afmetingen hebben.
    4. `A + C^T = ((0 , -14 , 16),(16 , 16 , -3))`
    1. `N = ((4 , 5 , 8 , 2),(5 , 3 , 7 , 1))`
    2. `Z = ((8 , 6 , 9 , 5),(10 , 5 , 11 , 4))`
    3. `N + Z = ((12 , 11 , 16 , 7),(15 , 8 , 18 , 5))` zijn de totale verkoopcijfers van beide filialen per type Smart per maand.
    4. Als je in de matrix van c de aantallen in de kolommen optelt, krijg je de totale verkoopcijfers per type Smart voor beide maanden samen. Tel je dan ook nog die vier getallen op, krijg je de totale verkoop aan Smarts in beide filialen over de maanden mei en juni.