Hellingsgrafiek
Inleiding
 Je kunt bij veel functies in een punt van de grafiek de helling van die grafiek berekenen.
Bij de meeste x-waarden hoort wel een hellingsgetal.
En dus kun je een grafiek maken van het hellingsgetal afhankelijk van de waarde van x.
Zo'n "hellingsgrafiek" zegt dan weer het nodige over de grafiek van de functie zelf.
Je kunt bij veel functies in een punt van de grafiek de helling van die grafiek berekenen.
Bij de meeste x-waarden hoort wel een hellingsgetal.
En dus kun je een grafiek maken van het hellingsgetal afhankelijk van de waarde van x.
Zo'n "hellingsgrafiek" zegt dan weer het nodige over de grafiek van de functie zelf.
Je leert nu:
- bij een gegeven grafiek een hellingsgrafiek schetsen;
- bij een gegeven functievoorschrift een hellingsgrafiek tekenen;
- uit een gegeven hellingsgrafiek gegevens over de bijbehorende functie aflezen;
- werken met tekenschema's van de hellingen van een functie;
- extremen van een functie berekenen vanuit de hellingsgrafiek.
Je kunt al:
- werken met functievoorschriften, functiewaarden berekenen;
- (toenemende, of afnemende, of constante) stijging en daling, maximum en minimum herkennen;
- met een differentiequotiënt de gemiddelde verandering op een interval uitrekenen;
- met een differentiaalquotiënt de veranderingssnelheid voor een bepaalde waarde berekenen.
Verkennen
En daar zit je dan op een stilstaande zeilwagen.
Als je het zeil hijst doet de windkracht je snelheid toenemen.
Bij een constante windkracht neemt de snelheid ook recht evenredig met die windkracht toe.
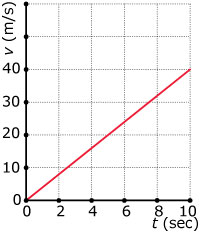
Hier zie je een snelheidsgrafiek bij een constante windkracht.
> Welke formule past bij deze grafiek?
> Schets de bijbehorende grafiek voor de afgelegde afstand.
> Kun je daar een formule bij verzinnen en zo berekenen hoeveel je na 20 seconden hebt afgelegd?
Uitleg
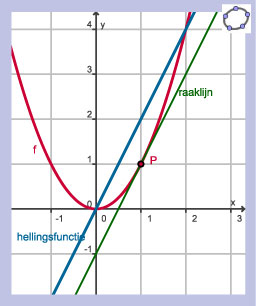 Je ziet hier de grafiek van de functie f(x) = x2 met daarin de raaklijn aan de grafiek in (1,1).
Je ziet hier de grafiek van de functie f(x) = x2 met daarin de raaklijn aan de grafiek in (1,1).
De richtingscoëfficiënt van die raaklijn bepaalt de helling van de grafiek bij x = 1.
Deze helling is de snelheid waarmee de functiewaarden veranderen op x = 1, aangegeven door het differentiaalquotiënt f'(1).
Als je de waarden van x verandert, veranderen ook de hellingswaarden f'(x).
Je kunt van die hellingswaarden een afzonderlijke grafiek maken: de hellingsgrafiek.
Je ziet hem hier ook getekend.
Beweeg punt P over de grafiek en ga na dat de hellingsgetallen van de raaklijn overeen komen met de functiewaarden van de hellingsgrafiek.
Je ziet hier de grafiek van de functie f(x) = x2 en zijn hellingsgrafiek.
Als je de grafiek van de functie f en die van zijn hellingsfunctie f' vergelijkt, dan valt op:
-
als de grafiek stijgend is, is de helling positief (en omgekeerd);
-
als de grafiek dalend is, is de helling negatief (en omgekeerd);
-
in toppen van de grafiek (en dus extremen van de functie) is de helling 0.
Deze eigenschappen kun je soms goed gebruiken om uit een hellingsgrafiek de karakteristieke eigenschappen
van de grafiek van f af te leiden.
Uit de hellingsgrafiek van een functie kun je bijvoorbeeld zijn (locale) extremen aflezen.
Een paar haken en ogen zitten er nog wel aan, maar daar ga je pas later op in...
‡
Opgaven
-
Bekijk de grafiek van `f(x)=x^2`. Stel dat je punt `P` over de grafiek kunt bewegen en zo in elk punt van de grafiek van `f` de raaklijn aan de grafiek bekijken en de helling `f'(x)` ervan aflezen.
Als je de grafiek op je grafische rekenmachine maakt, kun je met dy/dx in elk punt de helling bepalen.
-
Vul deze tabel in:
-
Met behulp van deze tabel kun je de hellingsgrafiek van deze functie tekenen.
Ga na, dat die hellingsgrafiek overeen komt met de blauwe grafiek in de figuur.
Theorie
Een functie y = f(x) heeft meestal in een punt van zijn grafiek een helling die wordt bepaald door het differentiaalquotiënt f'(x) in dat punt.
Van die hellingsgetallen kun je ook weer een grafiek maken.
Hier zie je de grafiek van een functie (rood) met de hellingsgrafiek (blauw), de grafiek van f'.
De functie f' noem je hellingsfunctie of afgeleide.
Je ziet:
-
als de hellingsfunctie positieve waarden heeft is de functie zelf stijgend;
-
als de hellingsfunctie negatieve waarden heeft is de functie zelf dalend;
-
in de waarden van x waarin de hellingsfunctie de waarde 0
heeft, heeft de grafiek van de functie zelf een horizontale raaklijn;
vaak gaat het daarbij om extremen van de functie.
Hieruit blijkt dat vooral het positief, negatief, of 0 zijn van de hellingsfunctie van belang is om het
verloop van de grafiek van een functie te beschrijven.
‡
Voorbeeld 1
Hier zie je de grafiek van de functie f met voorschrift f(x) = 0,5x4 – 4x2.
Teken de grafiek van de bijbehorende hellingsfunctie f'.
Antwoord
Maak met behulp van je grafische rekenmachine een tabel met hellingsgetallen:
| x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
| f'(x) |
–30 |
0 |
6 |
0 |
–6 |
0 |
30 |
En teken de bij deze tabel passende grafiek.
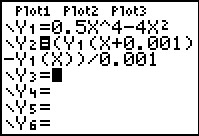
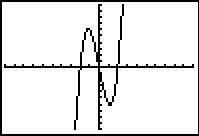
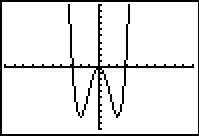
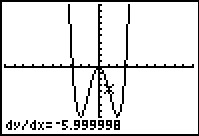
Je kunt ook direct je grafische rekenmachine een goede benadering van de hellingsgrafiek laten tekenen.
Daartoe laat je hem voor willekeurige x het differentiaalquotiënt benaderen door een differentiequotiënt
op het interval [x,x + 0,001] en daarvan een grafiek maken.
Hier zie je hoe dat bij een bepaalde functie kan.
‡
Voorbeeld 2
De hellingsfunctie zegt veel over het verloop van een grafiek.
Het gaat er dan vooral om waar de hellingen positief negatief of 0 zijn.
Daarvoor heb je geen hellingsgrafiek nodig, een tekenschema van de afgeleide is genoeg.
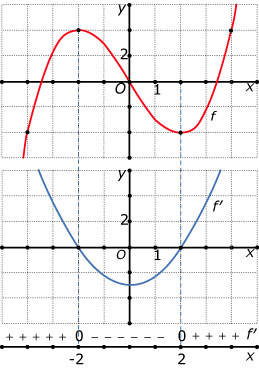
Je ziet hier een tekenschema van de hellingsfunctie van een onbekende functie f.

Schets een mogelijke grafiek van f.
Antwoord
Als de hellingsfunctie positief is de grafiek van f
stijgend, als de hellingsfunctie negatief is die grafiek dalend.
Welke waarden f(x) precies aanneemt is niet bekend.
Kies een startpunt, bijvoorbeeld (0,0).
De helling is daar negatief, dus de grafiek dalend.
Hoe steil, is onbekend.
Verder heeft de grafiek een maximum als x = –1 omdat daar de helling overgaat van positief in negatief.
Een minimum treedt op als x = 2 omdat dan de helling van negatief in positief verandert.
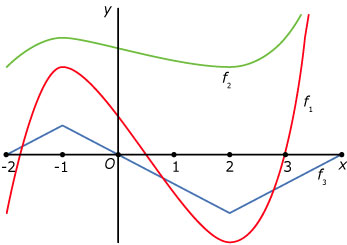
Hier zie je drie mogelijke grafieken.
Maar er zijn nog veel meer mogelijkheden.
De grafieken hoeven niet door (0,0) te gaan.
‡
Voorbeeld 3
Gegeven is de functie f(x) = x2.
Stel een voorschrift op voor de hellingsfunctie.
Antwoord
Je kunt dit doen door eerst een tabel met hellingsgetallen te maken:
| x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
| f'(x) |
–6 |
–4 |
–2 |
0 |
2 |
4 |
6 |
In de tabel lijkt het er op dat hellingsgetal telkens precies 2 keer de x-waarde is.
Je kunt de tabel nog uitbreiden om te bekijken of deze regelmaat blijft opgaan. Helaas kun je niet alle mogelijkheden uitproberen, maar het lijkt er op dat f'(x) = 2x.
Zeker kun je nog niet zijn.
Je kunt ook het differentiequotiënt berekenen op het interval [x,x + h]
en dan h steeds dichter naar 0 laten naderen.
Bij het onderwerp "Afgeleide functies" lees je daar meer over.
Voor nu is het leuk om eens te proberen of je daar zelf uit komt...
‡
Opgaven
-
Bekijk de Theorie nog eens.
Gegeven is de functie `f` met `f(x)=0,5x^3 - 6x`.
In elk punt heeft de grafiek van `f` een bepaalde helling, die wordt bepaald door het differentiaalquotiënt `f'(x)` in dat punt.
-
Vul deze tabel in:
-
Teken met behulp van deze tabel de hellingsgrafiek van de gegeven functie.
-
Welke waarde heeft `f'(x)` in de toppen van de grafiek van `f`?
-
Welke extreme waarde heeft `f'(x)` en wat betekent dit voor de grafiek van `f`?
- Er is verband tussen de grafiek en de hellingsgrafiek van een functie.
- Wat betekent het voor de grafiek van de functie als de hellingsgrafiek onder de `x`-as ligt?
- De functiewaarden zijn dan negatief.
- De grafiek is dan stijgend.
- De grafiek is dan dalend.
- De grafiek heeft dan een minimum.
- Soms is een grafiek toenemend stijgend. Hoe zie je dat aan de hellingsgrafiek?
- De hellingsgrafiek ligt dan boven de `x`-as.
- De hellingsgrafiek is stijgend.
- De hellingsgrafiek ligt boven de `x`-as en is stijgend.
- De hellingsgrafiek heeft een maximum.
- Hoe vind je de extremen van een functie uit de hellingsgrafiek?
- Je bekijkt voor welke waarden van `x` de hellingsgrafiek een maximum of een minimum heeft.
- Je bekijkt voor welke waarden van `x` de helling overgaat van positief in negatief (of omgekeerd).
- Je bekijkt voor welke waarden van `x` de helling de waarde `0` heeft.
- Dat kun je niet uit de hellingsgrafiek alleen aflezen.
-
In Voorbeeld 1 zie je hoe je met de grafische rekenmachine de hellingsgrafiek, de grafiek van de afgeleide, kunt benaderen.
Bekijk nu opnieuw de grafiek van `f(x)=0,5x^3 - 6x`.
-
Maak met je rekenmachine de grafiek van `f'(x)`.
-
Bepaal `f'(1)`. Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x=1`.
-
Bereken met je grafische rekenmachine het minimum van `f`.
Laat je grafische rekenmachine vervolgens het rechter nulpunt van `f'` berekenen.
Als het goed is vind je beide keren ongeveer dezelfde waarde van `x`. Waarom is dat zo? En waarom is dat "ongeveer"?
-
Voor een bewegend voorwerp geldt `a(t)=1,2t^2` waarin a de afgelegde afstand in m en `t` de tijd in seconden is.
- De snelheid van dit voorwerp na `5` seconden is `a'(5)`. Bereken deze snelheid in m/s en in km/h.
- De snelheid `v` is een functie van `t`, de hellingsfunctie `a'(5)`. Teken de grafiek van `v`.
- Stel een functievoorschrift op voor `v(t)`.
- Na hoeveel seconden beweegt het voorwerp met een snelheid van 50 km/h? (Rond af op één decimaal.)
-
In Voorbeeld 2 zie je dat een tekenschema van een afgeleide (hellingsfunctie) niet meer is dan een overzicht van waar deze afgeleide positief dan wel negatief is.
Bekijk de grafiek van de functie `y=x^3`.
- Welke van deze tekenschema’s is van de bijbehorende hellingsfunctie?
- Voor `x=0` is de helling van de grafiek van `f` gelijk aan 0.
Waarom heeft de grafiek van `f` geen extreme waarde voor `x=0`? (Geef alle goede antwoorden aan.)
- De grafiek is altijd stijgend, behalve bij `x=0`.
- Het tekenschema van de afgeleide wisselt bij `x=0` niet van teken.
- De functie heeft geen horizontale raaklijn voor `x=0`.
- De functie heeft wel een horizontale raaklijn voor `x=0` maar gaat daar niet over van stijgend in dalend.
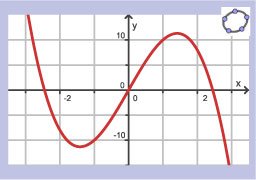
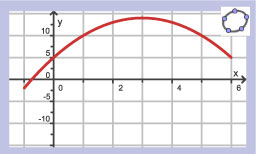
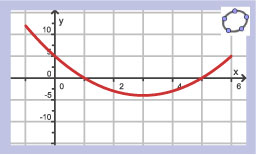
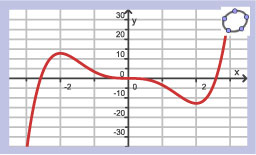
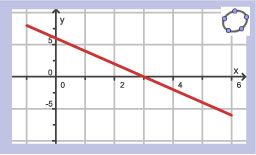 Hier zie je de hellingsgrafiek van functie `f`.
Hier zie je de hellingsgrafiek van functie `f`.
- De grafiek van `f` heeft:
- precies één extreme waarde van `6` voor `x=0`;
- geen extremen want de hellingsgrafiek is dalend;
- geen extremen want de grafiek van de functie zelf is ook dalend;
- een maximum voor `x=3`;
-
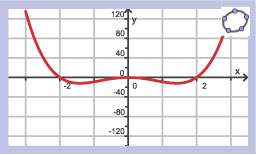
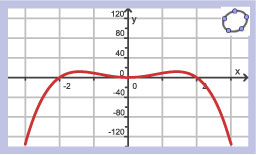
Als `f(0)=5`, welke van deze grafieken is dan een mogelijke grafiek van `f`?
-
Hier zie je een tekenschema van de hellingsfunctie van `f`. De grafiek van `f` gaat door `(0;0)`. Bekijk ook Voorbeeld 2.
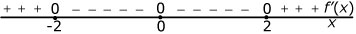
Welke van deze grafieken is een mogelijke grafiek van `f`?
-
In Voorbeeld 3 zie je hoe je bij een gegeven kwadratische functie een formule voor de hellingsfunctie kunt opstellen.
Gegeven de kwadratische functie `f(x)=x^2+4`.
Stel het voorschrift van de hellingsfunctie op met behulp van een tabel van `f'(x)`.
Verwerken
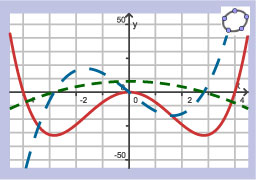 Hier zie je een grafiek (rood) en twee hellingsgrafieken (groen en blauw gestippeld).
Hier zie je een grafiek (rood) en twee hellingsgrafieken (groen en blauw gestippeld).
Welke hellingsgrafiek hoort bij de gegeven grafiek?
-
Kies telkens één van deze vier functies:
- `f(x)=-x^2+4`
- `g(x)=sqrt(x^2+3)`
- `h(x)=4/x`
- `k(x)=-x^4+4x`
- Bereken bij de gekozen functie het hellingsgetal voor `x=1`.
- Teken bij de gekozen functie de grafiek van de hellingsfunctie.
- Bepaal met behulp van de hellingsgrafiek de extremen van de gekozen functie.
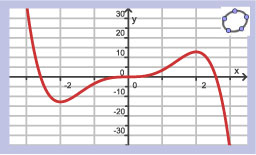
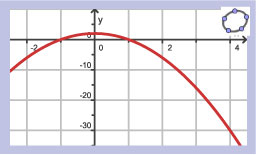 Je ziet hier de hellingsgrafiek van een functie `f`.
Je ziet hier de hellingsgrafiek van een functie `f`.
- Op welk interval stijgt de grafiek van `f`?
- Voor welke waarden van `x` heeft de grafiek van `f` een maximum?
- Kun je uit de hellingsgrafiek aflezen hoe groot dit maximum is?
- Neem aan dat `f(0)=2`. Teken nu de grafiek van `f`.
-
Je ziet hier het tekenschema van de hellingsfunctie van een functie `g`.
Schets een mogelijke grafiek van `g`.
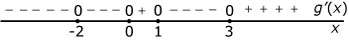
-
Een auto trekt op als het stoplicht op groen springt. Voor de afgelegde weg geldt: `s(t)=1,6t^2` waarin `s` de afgelegde weg in meters is en `t` de tijd in seconden is. Ga er vanuit dat deze auto niet hoeft te schakelen!
- De snelheid van deze auto wordt uitgedrukt in meters per seconde.
Teken de grafiek van de snelheid `v` van deze auto als functie van de tijd `t`.
- Als het goed is gegaan is je snelheidsgrafiek een rechte lijn. Stel een bijpassende formule op voor `v(t)`.
- Na hoeveel seconden is de snelheid meer dan 80 km//h? Geef je antwoord in één decimaal nauwkeurig.
- Gegeven is de functie `f(x)= 2x^3 - 6x^2 - 8x`.
- Met de grafische rekenmachine kun je de grafiek van `f` zo in beeld brengen dat alle drie de nulpunten en de twee toppen zichtbaar zijn. Toon aan dat deze grafiek de `x`-as snijdt in het punt `(4,0)`.
- Bereken het hellingsgetal van de grafiek in dit nulpunt.
- Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x=4`
- Teken de grafiek van de afgeleide van `f`.
- Met behulp van de grafiek van die afgeleide kun je de extremen van `f` berekenen.
Doe dat met behulp van je grafische rekenmachine in twee decimalen nauwkeurig.
-
Gegeven is de functie `f(x)= 0,5x^2 + 3x`.
Stel een voorschrift op voor de hellingsfunctie `f'(x)` door eerst een tabel van `f'` te maken.
Testen
-
Gegeven de functie `f(x)= x^2 - 4x`.
Maak een grafiek van de bijbehorende hellingsfunctie.
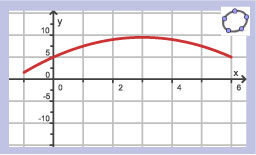
 Hier zie je een hellingsgrafiek van een functie `g`. De grafiek van deze functie gaat door `(2,4)`.
Hier zie je een hellingsgrafiek van een functie `g`. De grafiek van deze functie gaat door `(2,4)`.
Teken een mogelijke grafiek van `g`.
-
Dit is een tekenschema van de hellingsfunctie van een functie `f`.
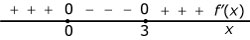
- Voor welke waarde van `x` heeft deze functie een maximum?
- Op welk interval is de grafiek van deze functie dalend?
- Maak een schets van een mogelijke grafiek van `f` die door `(0,1)` gaat.
 Je kunt bij veel functies in een punt van de grafiek de helling van die grafiek berekenen.
Bij de meeste x-waarden hoort wel een hellingsgetal.
En dus kun je een grafiek maken van het hellingsgetal afhankelijk van de waarde van x.
Zo'n "hellingsgrafiek" zegt dan weer het nodige over de grafiek van de functie zelf.
Je kunt bij veel functies in een punt van de grafiek de helling van die grafiek berekenen.
Bij de meeste x-waarden hoort wel een hellingsgetal.
En dus kun je een grafiek maken van het hellingsgetal afhankelijk van de waarde van x.
Zo'n "hellingsgrafiek" zegt dan weer het nodige over de grafiek van de functie zelf.


 Je ziet hier de grafiek van de functie f(x) = x2 met daarin de raaklijn aan de grafiek in (1,1).
Je ziet hier de grafiek van de functie f(x) = x2 met daarin de raaklijn aan de grafiek in (1,1).






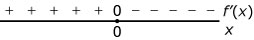
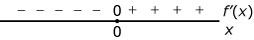
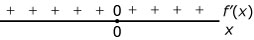

 Hier zie je de hellingsgrafiek van functie `f`.
Hier zie je de hellingsgrafiek van functie `f`.
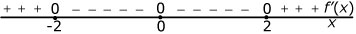
 Hier zie je een grafiek (rood) en twee hellingsgrafieken (groen en blauw gestippeld).
Hier zie je een grafiek (rood) en twee hellingsgrafieken (groen en blauw gestippeld). Je ziet hier de hellingsgrafiek van een functie `f`.
Je ziet hier de hellingsgrafiek van een functie `f`.
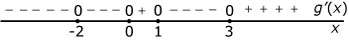
 Hier zie je een hellingsgrafiek van een functie `g`. De grafiek van deze functie gaat door `(2,4)`.
Hier zie je een hellingsgrafiek van een functie `g`. De grafiek van deze functie gaat door `(2,4)`.