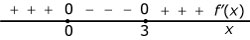Hellingsgrafiek
Inleiding
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Veranderingen > Hellingsgrafiek > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Veranderingen > Hellingsgrafiek > Inleiding
Probeer de vragen over de zeilwagen bij Verkennen zo goed mogelijk te beantwoorden.
Uitleg
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Veranderingen > Hellingsgrafiek > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Veranderingen > Hellingsgrafiek > Uitleg
Opgaven
-
Bekijk de applet met de grafiek van `f(x)=x^2`. Je kunt punt `P` over de grafiek bewegen en zo in elk punt van de grafiek van `f` de raaklijn aan de grafiek bekijken en de helling ervan aflezen.
-
Vul deze tabel in:
-
Met behulp van deze tabel kun je de hellingsgrafiek van deze functie tekenen.
Ga na, dat die hellingsgrafiek overeen komt met de blauwe grafiek in de applet.
Theorie
 www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Veranderingen > Hellingsgrafiek > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Veranderingen > Hellingsgrafiek > Theorie
Bestudeer eerst de Theorie en bekijk de applet goed.
Opgaven
-
In de applet in de Theorie zie je (een deel van) de grafiek van `f(x)=0,5x^3 - 6x`.
In elk punt heeft deze grafiek een bepaalde helling, die wordt bepaald door het differentiaalquotiënt `f'(x)` in dat punt.
-
Vul deze tabel in:
-
Met behulp van deze tabel kun je de hellingsgrafiek van deze functie tekenen.
Ga na, dat die hellingsgrafiek overeen komt met de blauwe grafiek in de applet.
-
Welke waarde heeft `f'(x)` in de toppen van de grafiek van `f`?
-
Welke extreme waarde heeft `f'(x)` en wat betekent dit voor de grafiek van `f`?
- Er is verband tussen de grafiek en de hellingsgrafiek van een functie.
- Wat betekent het voor de grafiek van de functie als de hellingsgrafiek onder de `x`-as ligt?
- De functiewaarden zijn dan negatief.
- De grafiek is dan stijgend.
- De grafiek is dan dalend.
- De grafiek heeft dan een minimum.
- Soms is een grafiek toenemend stijgend. Hoe zie je dat aan de hellingsgrafiek?
- De hellingsgrafiek ligt dan boven de `x`-as.
- De hellingsgrafiek is stijgend.
- De hellingsgrafiek ligt boven de `x`-as en is stijgend.
- De hellingsgrafiek heeft een maximum.
- Hoe vind je de extremen van een functie uit de hellingsgrafiek?
- Je bekijkt voor welke waarden van `x` de hellingsgrafiek een maximum of een minimum heeft.
- Je bekijkt voor welke waarden van `x` de helling overgaat van positief in negatief (of omgekeerd).
- Je bekijkt voor welke waarden van `x` de helling de waarde `0` heeft.
- Dat kun je niet uit de hellingsgrafiek alleen aflezen.
-
In Voorbeeld 1 zie je hoe je met de grafische rekenmachine de hellingsgrafiek, de grafiek van de afgeleide, kunt benaderen.
Bekijk nu opnieuw de grafiek van `f(x)=0,5x^3 - 6x`.
-
Maak met je rekenmachine de grafiek van `f'(x)`.
-
Bepaal `f'(1)`. Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x=1`.
(Controleer met behulp van de applet in de Theorie of je raaklijn correct is.)
-
Bereken met je grafische rekenmachine het minimum van `f`.
Laat je grafische rekenmachine vervolgens het rechter nulpunt van `f'` berekenen.
Als het goed is vind je beide keren ongeveer dezelfde waarde van `x`. Waarom is dat zo? En waarom is dat "ongeveer"?
-
Voor een bewegend voorwerp geldt `a(t)=1,2t^2` waarin a de afgelegde afstand in m en `t` de tijd in seconden is.
- De snelheid van dit voorwerp na `5` seconden is `a'(5)`. Bereken deze snelheid in m/s en in km/h.
- De snelheid `v` is een functie van `t`, de hellingsfunctie `a'(5)`. Teken de grafiek van `v`.
- Stel een functievoorschrift op voor `v(t)`.
- Na hoeveel seconden beweegt het voorwerp met een snelheid van 50 km/h? (Rond af op één decimaal.)
-
In Voorbeeld 2 zie je dat een tekenschema van een afgeleide (hellingsfunctie) niet meer is dan een overzicht van waar deze afgeleide positief dan wel negatief is.
Bekijk de grafiek van de functie `y=x^3`.
- Welke van deze tekenschema’s is van de bijbehorende hellingsfunctie?
- Voor `x=0` is de helling van de grafiek van `f` gelijk aan 0.
Waarom heeft de grafiek van `f` geen extreme waarde voor `x=0`? (Geef alle goede antwoorden aan.)
- De grafiek is altijd stijgend, behalve bij `x=0`.
- Het tekenschema van de afgeleide wisselt bij `x=0` niet van teken.
- De functie heeft geen horizontale raaklijn voor `x=0`.
- De functie heeft wel een horizontale raaklijn voor `x=0` maar gaat daar niet over van stijgend in dalend.
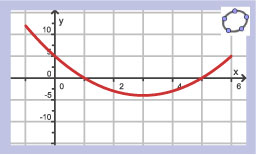
 Hier zie je de hellingsgrafiek van functie `f`.
Hier zie je de hellingsgrafiek van functie `f`.
- De grafiek van `f` heeft:
- precies één extreme waarde van `6` voor `x=0`;
- geen extremen want de hellingsgrafiek is dalend;
- geen extremen want de grafiek van de functie zelf is ook dalend;
- een maximum voor `x=3`;
-
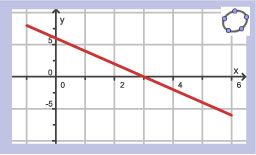
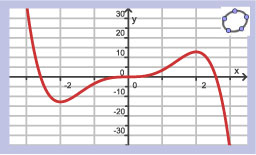
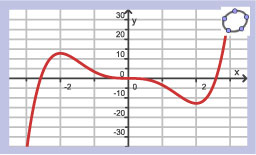
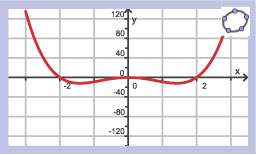
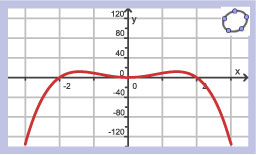
Als `f(0)=5`, welke van deze grafieken is dan een mogelijke grafiek van `f`?
-
Hier zie je een tekenschema van de hellingsfunctie van `f`. De grafiek van `f` gaat door `(0;0)`. Bekijk ook Voorbeeld 2.
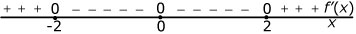
Welke van deze grafieken is een mogelijke grafiek van `f`?
-
In Voorbeeld 3 zie je hoe je bij een gegeven kwadratische functie een formule voor de hellingsfunctie kunt opstellen.
Gegeven de kwadratische functie `f(x)=x^2+4`.
Stel het voorschrift van de hellingsfunctie op met behulp van een tabel van `f'(x)`.
Verwerken
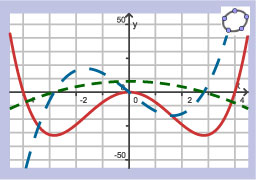 Hier zie je een grafiek (rood) en twee hellingsgrafieken (groen en blauw gestippeld).
Hier zie je een grafiek (rood) en twee hellingsgrafieken (groen en blauw gestippeld).
Welke hellingsgrafiek hoort bij de gegeven grafiek?
-
Kies telkens één van deze vier functies:
- `f(x)=-x^2+4`
- `g(x)=sqrt(x^2+3)`
- `h(x)=4/x`
- `k(x)=-x^4+4x`
- Bereken bij de gekozen functie het hellingsgetal voor `x=1`.
- Teken bij de gekozen functie de grafiek van de hellingsfunctie.
- Bepaal met behulp van de hellingsgrafiek de extremen van de gekozen functie.
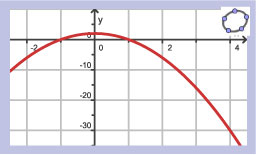 Je ziet hier de hellingsgrafiek van een functie `f`.
Je ziet hier de hellingsgrafiek van een functie `f`.
- Op welk interval stijgt de grafiek van `f`?
- Voor welke waarden van `x` heeft de grafiek van `f` een maximum?
- Kun je uit de hellingsgrafiek aflezen hoe groot dit maximum is?
- Neem aan dat `f(0)=2`. Teken nu de grafiek van `f`.
-
Je ziet hier het tekenschema van de hellingsfunctie van een functie `g`.
Schets een mogelijke grafiek van `g`.
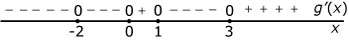
-
Een auto trekt op als het stoplicht op groen springt. Voor de afgelegde weg geldt: `s(t)=1,6t^2` waarin `s` de afgelegde weg in meters is en `t` de tijd in seconden is. Ga er vanuit dat deze auto niet hoeft te schakelen!
- De snelheid van deze auto wordt uitgedrukt in meters per seconde.
Teken de grafiek van de snelheid `v` van deze auto als functie van de tijd `t`.
- Als het goed is gegaan is je snelheidsgrafiek een rechte lijn. Stel een bijpassende formule op voor `v(t)`.
- Na hoeveel seconden is de snelheid meer dan 80 km//h? Geef je antwoord in één decimaal nauwkeurig.
- Gegeven is de functie `f(x)= 2x^3 - 6x^2 - 8x`.
- Met de grafische rekenmachine kun je de grafiek van `f` zo in beeld brengen dat alle drie de nulpunten en de twee toppen zichtbaar zijn. Toon aan dat deze grafiek de `x`-as snijdt in het punt `(4,0)`.
- Bereken het hellingsgetal van de grafiek in dit nulpunt.
- Stel een vergelijking op van de raaklijn aan de grafiek van `f` voor `x=4`
- Teken de grafiek van de afgeleide van `f`.
- Met behulp van de grafiek van die afgeleide kun je de extremen van `f` berekenen.
Doe dat met behulp van je grafische rekenmachine in twee decimalen nauwkeurig.
-
Gegeven is de functie `f(x)= 0,5x^2 + 3x`.
Stel een voorschrift op voor de hellingsfunctie `f'(x)` door eerst een tabel van `f'` te maken.
Testen
-
Gegeven de functie `f(x)= x^2 - 4x`.
Maak een grafiek van de bijbehorende hellingsfunctie.
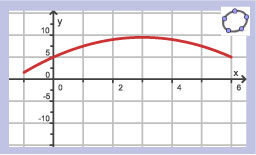
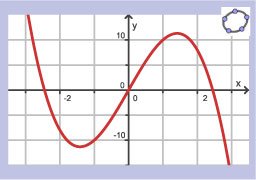 Hier zie je een hellingsgrafiek van een functie `g`. De grafiek van deze functie gaat door `(2,4)`.
Hier zie je een hellingsgrafiek van een functie `g`. De grafiek van deze functie gaat door `(2,4)`.
Teken een mogelijke grafiek van `g`.
-
Dit is een tekenschema van de hellingsfunctie van een functie `f`.
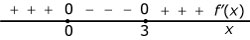
- Voor welke waarde van `x` heeft deze functie een maximum?
- Op welk interval is de grafiek van deze functie dalend?
- Maak een schets van een mogelijke grafiek van `f` die door `(0,1)` gaat.

![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Veranderingen > Hellingsgrafiek > Inleiding
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Veranderingen > Hellingsgrafiek > Inleiding![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Veranderingen > Hellingsgrafiek > Uitleg
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Veranderingen > Hellingsgrafiek > Uitleg![]() www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Veranderingen > Hellingsgrafiek > Theorie
www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Veranderingen > Hellingsgrafiek > Theorie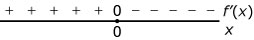
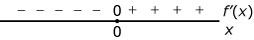
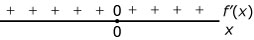

 Hier zie je de hellingsgrafiek van functie `f`.
Hier zie je de hellingsgrafiek van functie `f`.

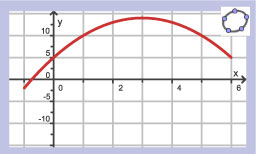
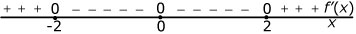
 Hier zie je een grafiek (rood) en twee hellingsgrafieken (groen en blauw gestippeld).
Hier zie je een grafiek (rood) en twee hellingsgrafieken (groen en blauw gestippeld). Je ziet hier de hellingsgrafiek van een functie `f`.
Je ziet hier de hellingsgrafiek van een functie `f`.
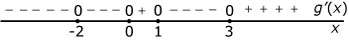
 Hier zie je een hellingsgrafiek van een functie `g`. De grafiek van deze functie gaat door `(2,4)`.
Hier zie je een hellingsgrafiek van een functie `g`. De grafiek van deze functie gaat door `(2,4)`.