Hellingsgrafiek

Antwoorden bij de opgaven

1. 1. x	-3	-2	-1	0	1	2	3
      f'(x)	–6	–4	–2	0	2	4	6

   2. -

2. 1. x	-3	-2	-1	0	1	2	3
      f'(x)	7,5	0	–4,5	–6	–4,5	0	7,5

   2. 
   3. 0
   4. `f'` heeft een minimum van `-6` voor `x=0`.
      De grafiek van `f` gaat daar van toenemend dalend over naar afnemend dalend.
3. 1. C
   2. C
   3. B
4. 1. GR: Y1=0.5X^3-6X en Y2=(Y1(X+0.0001)-Y1(X))/0.0001
   2. `f'(1)=-4,5` en `f(1)=-5,5` dus de raaklijn wordt: `y=-4,5x - 1`
   3. Het minimum van `f` is `-8` en zit bij `x=2`.
      Je GR rekent dit minimum waarschijnlijk wel netjes uit, maar het nulpunt van de hellingsgrafiek kon wel eens een benadering opleveren omdat je met een benadering van de hellingsgrafiek werkt.
5. 1. `a'(5)=12` m/s en dat is 43,2 km/h
   2. De grafiek van `v(t)` is een rechte lijn door `(0,0)` en `(5,12)`.
   3. `v(t)=2,4t`
   4. `2,4t~~13,89` oplossen geeft `t~~5,8` seconden.
6. 1. C
   2. A, B, D
7. 1. D
   2. Alleen B is goed, de helling voor `x=0` moet 6 zijn.
8. B
9. `f'(x) = 2x`
10. De blauwe (lang gestippelde) grafiek.
11. 1. `f'(1)=-2`; `g'(1)=0,5`; `h'(1)=-4`; `k'(1)=0`
    2. Gebruik je GR.
    3. Nulpunten van de hellingsgrafieken opzoeken.
       `f`: max.`f(0)=4`
       `g`: min.`g(0)=sqrt(3)`
       `h`: geen extremen
       `k`: max.`k(1)=3`
12. 1. `(:-1,1:)`
    2. `x=1`
    3. Nee, daarvoor moet je het functievoorschrift van `f` weten.
    4. De juiste grafiek is die van `f(x)=-2/3 x^3 + 2x + 2`, maar dat kun je zelf (waarschijnlijk) niet afleiden.
       Het is goed genoeg als je grafiek door `(0,2)` gaat en een maximum heeft voor `x=1` en een minimum voor `x=-1`.
13. 
    
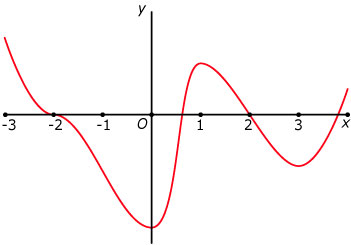
14. 1. Gebruik je GR
    2. `v(t)=3,2t`
    3. `3,2t~~22,22` oplossen geeft `t~~6,9` s
15. 1. -
    2. 40
    3. Gebruik je GR
    4. Nulpunten van de hellingsgrafiek bepalen en de gevonden `x`-waarden invullen in `f`.
       Je vindt: min.`f(2,53)~~-26,26` en max.`f(-0,52)~~2,26`.
16. `f'(x)=x+3`
17. Gebruik je GR. Je vindt: `f'(x) = 2x - 4`.
18. De grafiek van `g` moet in ieder geval door `(2,4)` gaan en drie extremen hebben: maxima voor `x~~-2,4` en `x~~2,4` en een minimum voor `x=0`.
19. 1. `x=0`
    2. `(:0,3:)`
    3. De grafiek van `f` moet in ieder geval door `(0,1)` gaan en twee extremen hebben: een maxima voor `x=0` en een minimum voor `x=3`.