Differentiaalquotiënt

Inleiding

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Veranderingen > Differentiaalquotiënt > Inleiding

Probeer de vragen bij Verkennen zo goed mogelijk te beantwoorden.

Uitleg

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Veranderingen > Differentiaalquotiënt > Uitleg

Opgaven

Voor een versnellende zeilwagen geldt `a=1,8t^2` waarin `a` de afgelegde afstand in meter en `t` de tijd in seconden is. Bekijk eerst bij de uitleg hoe de snelheid van een andere zeilwagen op een bepaald tijdstip wordt gevonden met behulp van een rij van differentiequotiënten.

De snelheid op `t=3` is
1. hetzelfde als de gemiddelde snelheid over de eerste 3 seconden;
2. groter dan de gemiddelde snelheid over de eerste 3 seconden;
3. kleiner dan de gemiddelde snelheid over de eerste 3 seconden.

Bereken de differentiequotiënten op het interval `[3; 3+h]`.

interval	differentiequotiënt
[3; 3,1]
[3; 3,01]
[3; 3,001]
[3; 3,0001]

Hoe groot is nu de snelheid op `t=3`?
Hoe is de snelheid op `t=3` zichtbaar in de grafiek?
1. als hellingsgetal van de koorde op het interval `[0,3]`;
2. als hellingsgetal van de koorde op het interval `[3;3,0001]`;
3. als hellingsgetal van de raaklijn aan de grafiek in het punt met `t=3`;
4. als uitkomst bij `t=3`.

Theorie

www.math4all.nl > MAThADORE-basic HAVO/VWO > 4/5/6 VWO wi-c > Veranderingen > Differentiaalquotiënt > Theorie

Bestudeer eerst de Theorie. In de opgaven wordt je naar de Voorbeelden verwezen.

Opgaven

In Voorbeeld 1 zie je hoe je bij een gegeven functie `f` het differentiaalquotiënt voor een bepaalde `x`-waarde kunt berekenen.
1. Wat betekent dit getal voor de grafiek? (Geef alle goede antwoorden.)
  1. het hellingsgetal van de grafiek voor die `x`-waarde;
  2. het hellingsgetal van de koorde op het interval `[0;x]`;
  3. de richtingscoëfficiënt van de raaklijn aan de grafiek voor die `x`-waarde;
  4. de `y`-waarde bij die waarde van `x`.
2. Welke betekenis heeft dit getal voor de functiewaarden?
  1. de grootte van de functiewaarde bij die waarde van `x`;
  2. de snelheid waarmee de functiewaarden veranderen voor die waarde van `x`;
  3. de gemiddelde verandering van de functiewaarden.
3. Bekijk de grafiek van `f(x)=0,5x^3+2`. Je wilt het differentiaalquotiënt bepalen voor `x=1`.
  Maak een rij met differentiequotiënten op het interval `[1,1+h]` waarin `h` achtereenvolgens de waarden `1`, `0,01`, `0,001` en `0,0001` heeft.
4. Hoe groot is dus het differentiaalquotiënt voor `x=1`?

Bekijk Voorbeeld 2.
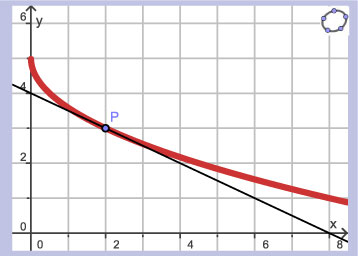
Hier zie je een deel van een grafiek met een raaklijn aan de grafiek voor `x=2`.
1. Bepaal het differentiaalquotiënt voor `x=2` met behulp van de figuur.
2. Stel een vergelijking van de getekende raaklijn op.
3. De grafiek hoort bij de functie `f(x)=5-sqrt(2x)`. Controleer je antwoord bij a door het differentiaalquotiënt door de grafische rekenmachine te laten bepalen.

Gegeven is de functie `f(x)=0,6x^2+1`.
1. Bekijk de grafiek van deze functie op het interval `[-4,4]`. Laat zien, dat het punt `(2;3,4)` op de grafiek van deze functie ligt.
2. Bereken `f'(2)` op de manier van Voorbeeld 3.
3. Stel een vergelijking op voor de raaklijn aan de grafiek in `(2;3,4)`.
4. Er is een punt op de grafiek waarin de helling van de raaklijn precies het tegenovergestelde is van die bij a. Welk punt is dat? Licht je antwoord toe.
5. In welk punt van de grafiek is de helling `0`?

Verwerken

Een steen valt van een loodrechte rotswand `500`m naar beneden. Voor de afgelegde weg `y` (in m) geldt de formule `y(t)=4,9t^2` waarin `t` de tijd in seconden is, tenminste zolang de steen nog aan het vallen is en niet op de grond terecht is gekomen.
1. Bereken de gemiddelde snelheid van de steen gedurende de eerste `5` seconden.
2. Bereken de snelheid van de steen na precies `5` seconden. (Gebruik een rij van differentiequotiënten en controleer je antwoord met de grafische rekenmachine.)
3. Bereken de snelheid waarmee de steen op de grond terecht komt.

Bekijk de grafiek van de functie `f(x)=5x^2-x^3` op je grafische rekenmachine.
1. Bereken het hellingsgetal voor `x=2` met behulp van een rij differentiequotiënten.
2. Je kunt van tevoren aan de grafiek zien of het hellingsgetal positief of negatief is. Waaraan kun je dat zien?
3. Stel een vergelijking op van de raaklijn voor `x=2` aan de grafiek van `f`.

Gegeven op het interval `[-5,5]` de functie met voorschrift `g(x)=4/x`.
1. Bereken de veranderingssnelheid van `g(x)` voor `x=1`.
2. Er is een punt van de grafiek van `g` waar de helling dezelfde waarde heeft als die in `(1,4)`. Welk punt is dat? Licht je antwoord toe.
3. Voor `x=0` heeft de functie `g` geen functiewaarde. Wat betekent dit voor de helling? En wat is er met de grafiek aan de hand?

De concentratie `C` van een bepaalde stof die is opgelost in water, neemt met de tijd af volgens de formule `C(t)=10*0,9^t`. Hierin is `C` in g/L (gram per liter) en `t` in uren.
1. Er verdwijnt niet elk uur een even grote hoeveelheid van deze stof uit het water. Hoe komt dat?
2. Hoeveel gram van deze stof verdwijnt er gemiddeld in de eerste `5` uren? (Geef je antwoord in twee decimalen nauwkeurig.)
3. De vervalsnelheid van deze stof op `t=5` is niet gelijk aan de hoeveelheid die er tot dan toe gemiddeld per uur is verdwenen. Bereken deze vervalsnelheid in twee decimalen nauwkeurig.

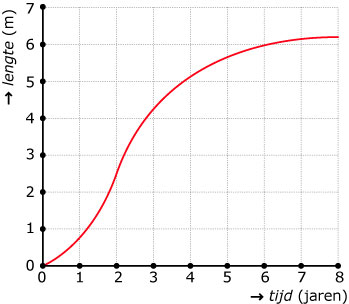Hier zie je een grafiek van de lengtegroei van een boom in de loop van de jaren.
1. Hoeveel meter per jaar groeit deze boom gemiddeld, gerekend over de eerste `5` jaar?
2. Hoeveel bedraagt de groeisnelheid na precies `5` jaar? Geef een zo nauwkeurig mogelijke schatting.
3. Op welk tijdstip is de groeisnelheid het grootst? Licht je antwoord toe.
4. Welke waarde krijgt de groeisnelheid uiteindelijk zolang de boom gezond blijft?

De baan van een vuurpijl is bij benadering parabolisch tot hij uit elkaar spat. Hier zie je een mogelijke baan. Bij deze baan past de formule `h(x)=-x^2+10x` waarin zowel `h` als `x` in meters worden uitgedrukt.
1. Welke helling heeft de baan als de vuurpijl wordt afgeschoten?
2. In welk punt van de baan is de helling `0`?
3. Als de pijl horizontaal `8` meter heeft afgelegd, spat hij uiteen. Hoe hoog zit hij dan en welke helling heeft zijn baan?

Testen

Een hoeveelheid `H` (in kilogram) groeit exponentieel volgens de formule `H(t)=2500*1,2^t` met `t` in dagen.
1. Bereken de gemiddelde toename van deze hoeveelheid op het interval `[0,4]`.
2. Bereken de toenamesnelheid van deze hoeveelheid op `t=4` met behulp van een rij van differentiequotiënten. Controleer je antwoord met de grafische rekenmachine.
3. Deze toenamesnelheid op `t=4` kun je in de grafiek aangeven. Leg uit hoe dat gaat.
  1. Eerst een raaklijn tekenen aan de grafiek in het punt met `t=4`. Vervolgens de richtingscoëfficiënt van die raaklijn aangeven in de figuur.
  2. Een rechte lijn tekenen tussen `(0,2500)` en `(4,5184)`. Vervolgens het hellingsgetal van die lijn berekenen.
  3. Een koorde tekenen tussen `(4,5184)` en `(5,6221)`. Vervolgens het hellingsgetal van die lijn berekenen.

Bekijk de grafiek van de functie `f(x)=4-sqrt(x)` met `x>=0`.
1. Het differentiaalquotiënt voor elke positieve waarde van `x` is
  1. ook positief;
  2. negatief;
  3. dalend.
2. Bereken `f'(4)` met behulp van een rij differentiequotiënten. Controleer daarna je antwoord met van de grafische rekenmachine.
3. Je kunt het differentiaalquotiënt `f'(4)` ook schatten met behulp van de grafiek van `f` . Dat doe je door (geef alle goede mogelijkheden):
  1. De richtingscoëfficiënt van de raaklijn aan de grafiek voor `x=4` te schatten door twee punten op die raaklijn af te lezen.
  2. Twee punten op de grafiek te bepalen die dicht bij elkaar te liggen en het bijbehorende differentiequotiënt te berekenen.
  3. De grafische rekenmachine het hellingsgetal `(text(d) y)/(text(d) x)` laten berekenen voor `x=4`.