Differentiequotiënt

Inleiding

Je hebt veranderingen in grafieken leren beschrijven in woorden en met toenamediagrammen. Bij toenamediagrammen moet je met een vaste stapgrootte werken. Maar als je wilt nagaan of een wielrenner de eerste 10 minuten gemiddeld net zoveel heeft afgelegd dan de volgende 15 minuten, heb je met ongelijke intervallen te doen. In dat geval werk je met gemiddelde veranderingen.

Je leert nu:

de gemiddelde veranderingssnelheid berekenen (dat heet differentiequotiënt);
de gemiddelde veranderingssnelheid in de grafiek aangeven;
werken met toepassingen van de gemiddelde veranderingssnelheid.

Je kunt al:

werken met functievoorschriften, functiewaarden berekenen;
(toenemende, of afnemende, of constante) stijging en daling, maximum en minimum herkennen;
werken met toenamediagrammen.

Verkennen

Bij een wielrenner in een tijdrit worden op bepaalde plaatsen tussentijden genoteerd. Die vind je in de tabel.

tijd (min.)	0	10	18	34	44	60	78	94
afstand (km)	0	8	12	18	23	29	37	45

> Is hij de eerste 8 km gemiddeld sneller of langzamer dan in de volgende 4 km? Waaraan zie je dat?
> Waarom is er bij deze situatie eigenlijk geen toenamediagram te maken?

Je maakt bij deze tabel een grafiek door de punten met lijnstukken te verbinden. Op de horizontale as komt de tijd, op de verticale as de afgelegde afstand. Niet alle lijnstukken zijn even steil.

> Hoe kun je de helling van zo'n lijnstuk in een getal uitdrukken?
> Bereken de helling van het lijnstuk dat hoort bij de periode vanaf de 12^e tot en met de 18^e km.
> Wat betekent het getal dat je zojuist hebt gevonden voor de wielrenner?

Uitleg

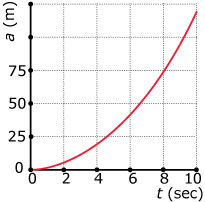
Je ziet hier een zeilwagen op het strand. Als zo'n zeilwagen start en de windkracht is constant, dan neemt zijn snelheid recht evenredig met de tijd toe.
Voor de afgelegde afstand a (in m) geldt: a = 1,2t².
Hierin is t de tijd in seconden.

Na 1 seconde is de afgelegde afstand a(1) = 1,2 m.
Na 4 seconden is de afgelegde afstand a(1) = 19,2 m.

In die 4 – 1 = 3 seconden heeft de zeilwagen
a(4) – a(1) = 19,2 – 1,2 = 18 m afgelegd.
De gemiddelde verandering van de afstand per seconde (de gemiddelde snelheid) is: `18/3=6` m/s (meter per seconde).

Je berekent een gemiddelde snelheid door het verschil in afstand te delen door het verschil in tijd.
Dat schrijf je als: gemiddelde snelheid = `(Delta afstand)/(Delta tijd)`

Het teken Δ (een Griekse letter D) staat voor differentie, wat verschil betekent.
Dit getal is de helling van het lijnstuk tussen de punten die horen bij 1 seconde en bij 4 seconden.

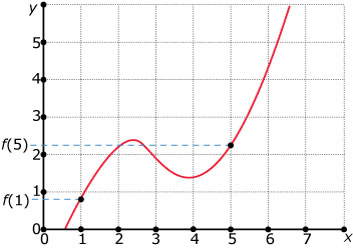
In het algemeen heb je te maken met y als functie van x: y = f(x).

Stel dat x toeneemt van bijvoorbeeld x = 1 tot x = 5.
Dan is de toename Δx = 5 – 1 = 4.
Tegelijk verandert y van f(1) naar f(5).
Dus een toename (of afname) van f(5) – f(1).

Gemiddeld (dus per eenheid van x) verandert y op het interval [1, 5] met:

`(Delta y)/(Delta x) = (f(5)-f(1))/(5-1)`

En dit is een deling van twee verschillen, een zogenaamd differentiequotiënt ("differentie" is "verschil" en een quotiënt is de uitkomst van een deling).
Op deze manier bereken je bij elke functie de gemiddelde verandering (van y op een gegeven interval.

‡

Opgaven

Voor de afgelegde afstand `s` van een versnellend voorwerp (in m) geldt: `s=1,2t^2`. Hierin is `t` de tijd in seconden. Bekijk eventueel de Uitleg.
1. Je wilt de gemiddelde snelheid op het tijdsinterval `[0,6]` berekenen. Bereken eerst `Delta t`.
2. Bereken vervolgens het verschil in afstand `Delta s`.
3. Hoeveel bedraagt dus de gemiddelde snelheid op het interval `[0,6]`?
4. Bereken ook de gemiddelde snelheid op het interval `[6,10]`
5. Op welk van beide intervallen bewoog het voorwerp bewoog gemiddeld het snelst?

Theorie

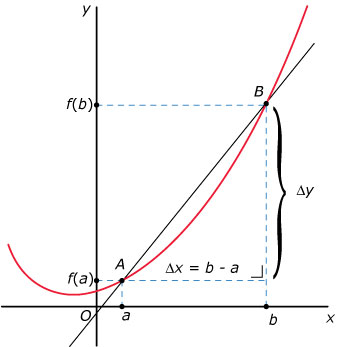
Hier zie je een deel van de grafiek van de functie y = f(x).

De gemiddelde verandering van de functie f op het interval [a, b] is:

`(Delta y)/(Delta x) = (f(b)-f(a))/(b-a)`

Deze verhouding van het verschil van de functiewaarden in de uiteinden van het interval en het verschil van beide x-waarden noem je het differentiequotiënt van de functie f op het interval [a, b].

In de grafiek van f is dit differentiequotiënt gelijk aan de richtingscoëfficiënt van de lijn door A(a, f(a)) en B(b, f(b)).
Die lijn heet de koorde AB.

‡

Voorbeeld 1

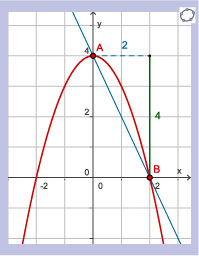
Gegeven is de functie f met voorschrift f(x) = 4 – x².

Bereken het differentiequotiënt op het interval [0,2] en beschrijf de betekenis van dit getal.

Antwoord

Het differentiequotiënt op het interval [0,2] is:

`(Delta y)/(Delta x) = (f(2)-f(0))/(2-0) = (0-4)/2 = -2`

Je ziet dat het differentiequotiënt gelijk is aan het hellingsgetal van het lijnstuk AB. Het is de gemiddelde verandering van de functiewaarden op het interval [0,2]. Het geeft dus de toename of de afname van f(x) per eenheid van x weer.

‡

Voorbeeld 2

Een hardloper houdt onderweg zijn tussentijden bij:

tijd t (min.)	0	10	15	21
afstand s (km)	0	3,5	5,5	8,0

Gedurende de eerste 10 minuten liep hij 3,5 km.
Gedurende de volgende 5 minuten liep hij 2 km.

Op welk van deze twee tijdsintervallen liep hij het best?

Antwoord

Op het interval [0,10] geldt: `(Delta s)/(Delta t) = (3,5-0)/(10-0) = 0,35`
Daar is de gemiddelde snelheid 0,35 km/min.

Op het interval [10,15] geldt: Op het interval [0,10] geldt: `(Delta s)/(Delta t) = (5,5-3,5)/(15-10) = 0,40`
Daar is de gemiddelde snelheid 0,40 km/min.

Hoewel hij dus op het tweede tijdsinterval een kleinere afstand aflegt, is zijn gemiddelde snelheid er hoger. Met behulp van differentiequotiënten kun je de prestaties eerlijk vergelijken.

‡

Voorbeeld 3

Toon aan dat bij de lineaire functie y = 3x + 5 elk differentiequotiënt gelijk is.

Antwoord

Neem twee punten op de grafiek: P(p,3p + 5) en Q(q,3q + 5).

Het differentiequotiënt op het interval [p,q] is dan:

`(Delta y)/(Delta x) = (3q+5-(3p+5))/(q-p) = (3q-3p)/(q-p) = (3(q-p))/(q-p) = 3` zolang p ≠ q.

En dat is precies de constante richtingscoëfficiënt van de gegeven lineaire functie.

‡

Opgaven

Bekijk eerst Voorbeeld 1. Gegeven is nu de functie `f(x)=(x-2)^2+3`. Je kunt het differentiequotiënt op het interval `[1,5]` in stappen berekenen.
1. Bereken eerst `Delta x`.
2. Bereken vervolgens `Delta y=f(5)-f(1)`.
3. Tenslotte bereken je het differentiequotiënt door delen.
4. Het is ook een goede oefening om de berekening in één keer te doen. Bereken het differentiequotiënt van `f` op het interval `[-2,4]`. (Rond af op één decimaal)

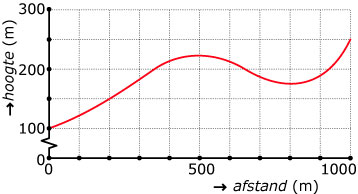Bij het begin van een berghelling staat een waarschuwingsbord met daarop een helling van 15%. Deze grafiek geeft die berghelling weer. Horizontaal is de afstand uitgezet die je hemelsbreed hebt afgelegd en verticaal de hoogte waarop je je dan bevindt.
1. Hoeveel bedraagt de gemiddelde hoogteverandering per meter bij zo'n hellingspercentage?
2. Hoeveel bedraagt de gemiddelde hoogteverandering gerekend over de gehele berghelling?
3. Klopt het waarschuwingsbord?
4. Hoeveel bedraagt de gemiddelde hoogteverandering op het interval `[400;500]` ongeveer?
5. Schat de steilste helling van deze berghelling.

Bekijk eerst Voorbeeld 3.
1. Elke constante functie heeft de vorm `f(x)=c`. Toon aan dat de gemiddelde helling van zo'n functie op elk interval gelijk is aan `0`.
2. Het prototype van alle kwadratische functies is de functie `f(x)=x^2`. Druk de gemiddelde helling van zo’n functie op het interval `[a,b]` uit in `a` en `b`. (Schrijf de gevonden uitdrukking zo eenvoudig mogelijk.)

Verwerken

Je ziet hier een aantal punten op een grafiek.
1. Bereken de gemiddelde helling van de koorde `AB`.
2. Bereken de gemiddelde helling van de koorde `CF`.
3. Bij twee van de getekende punten hoort een differentiequotiënt van `0`.
  Welke twee punten zijn dat? (Er zijn twee mogelijkheden!).
4. Punt `F` heeft een kleinere `y`-waarde dan punt `C`. Hoe kun je dat aan het differentiequotiënt op het interval `[1,4]` zien?

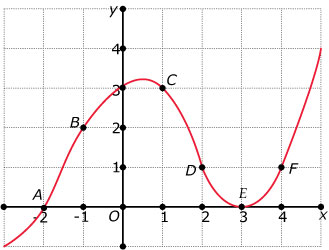
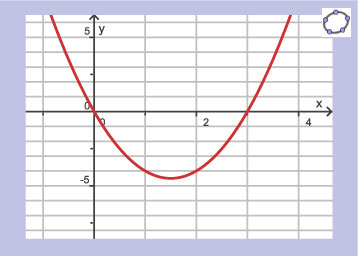Gegeven is deze grafiek.
Bereken het differentiequotiënt op het interval `[1,3]`.

Gegeven de functie `f(x)=x^3-3x^2+6` met domein `[2,4]`.
1. Bereken het differentiequotiënt op het interval `[0,2]`.
2. Bereken het differentiequotiënt op het interval `[-1,2]`.
3. Wat valt je bij b op? Kun je dat verklaren?
4. Noem een interval waarop de grafiek van `f` stijgend is. En bereken op dat interval het differentiequotiënt.

Het afkoelen van een kopje koffie hangt af van de temperatuur van de koffie bij het inschenken en de kamertemperatuur. Ook de vorm en het materiaal waarvan het kopje is gemaakt heeft invloed. De formule `T(t)=20+70*0,82^t` geeft de temperatuur van de koffie.
1. Wat is de temperatuur van de koffie bij het inschenken?
2. Hoeveel graden daalt de temperatuur van de koffie gemiddeld in de eerste vijf minuten?
3. Bereken ook in één decimaal nauwkeurig hoeveel de temperatuur gemiddeld daalt in de volgende vijf minuten.
4. De temperatuur van de koffie daalt van `t=0` tot `t=5` sneller dan van `t=5` tot `t=10`. Leg uit hoe je dit aan de differentiequotiënten bij b en c kunt zien. Geef er ook een natuurkundige verklaring voor.

Gegeven is de functie `f(x)=3x^2`.
Toon aan dat het differentiequotiënt op elk interval `[a,a+1]` gelijk is aan `6*a+3`.

Testen

Bij een wielrenner in een tijdrit worden op bepaalde plaatsen tussentijden genoteerd. Die vind je in de tabel.

tijd t (min)	0	10	18	34	44	60	78	94
afstand a (km)	0	8	12	18	23	29	37	45

Bereken het differentiequotiënt op het tijdsinterval `[0;10]`.
Welke betekenis heeft dit getal voor de wielrenner?
1. Het is de afgelegde afstand in die periode.
2. Het is de snelheid gedurende die periode.
3. Het is de gemiddelde snelheid gedurende die periode.
Je maakt bij deze tabel een grafiek door de punten met lijnstukken te verbinden. Op de horizontale as komt de tijd t in minuten, op de verticale as de afgelegde afstand `a` in km. Bereken het hellingsgetal van het lijnstuk dat hoort bij het interval `[44,60]`.
Bereken voor het tijdsinterval `[18,44]` de waarde `(Delta a)/(Delta t)` in twee decimalen nauwkeurig.
Welke betekenis hebben de bij c en d gevonden getallen voor de grafiek? (Geef alle goede antwoorden.)
1. Ze geven de helling weer van het lijnstuk door de punten op de grafiek bij het begin en het eind van het tijdsinterval.
2. Ze geven de totale toename van de afstand weer op het tijdsinterval.
3. Ze geven de gemiddelde toename van de afstand per minuut weer op het tijdsinterval.

Gegeven de functie `f(x)=0,5x^4`.
Bereken het differentiequotiënt op het interval `[0,2]`.

Gegeven de functie `f(x)=0,5x^2`.
Bereken het differentiequotiënt op het interval `[p,2p]` (met `p!=0`).